GPs for GLMs
+ Spatial Data

Lecture 17

Dr. Colin Rundel

GPs and GLMs

Logistic Regression

A typical logistic regression problem uses the following model,

\[ \begin{aligned} y_i &\sim \text{Bern}(p_i)\\ \text{logit}(p_i) &= \boldsymbol{X}\,\boldsymbol{\beta} \\ &= \beta_0 + \beta_1 \, x_{i1} + \cdots + \beta_k \, x_{ik} \end{aligned} \]

there is no reason that the linear equation above can’t contain thing like random effects or GPs

\[ \begin{aligned} y_i &\sim \text{Bern}(p_i) \\ \text{logit}(p_i) &= \eta_i = \boldsymbol{X}\,\boldsymbol{\beta} + w(\boldsymbol{x}) \\ w(\boldsymbol{x}) &\sim N(0,\Sigma) \end{aligned} \]

A toy example

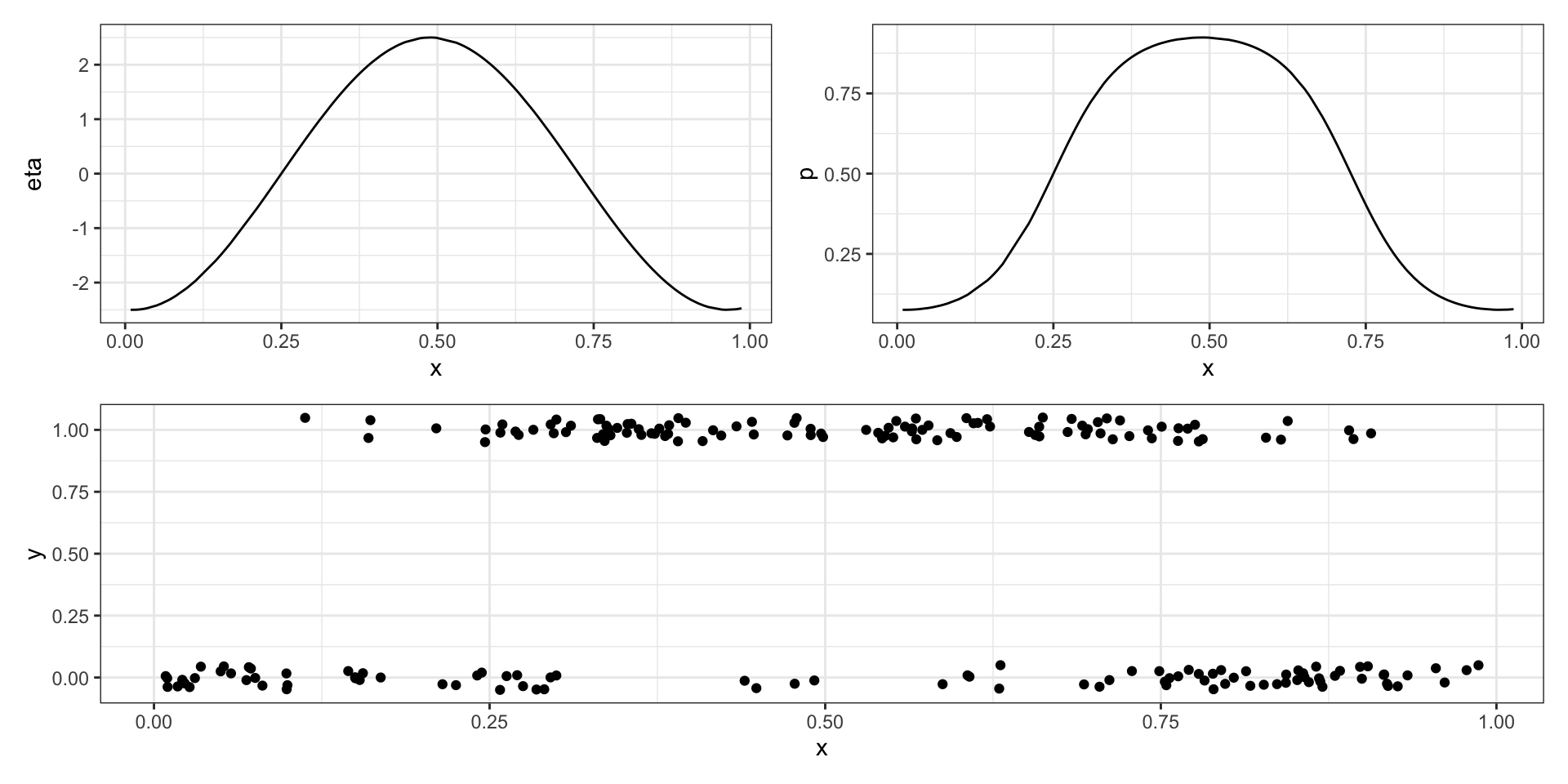
Model fitting

m = gpglm(
  y~1, family="binomial",
  data = d, coords = c("x"),
  cov_model = "exponential",
  starting=list(
    "beta"=0, "phi"=3/0.1, "sigma.sq"=1, "w"=0
  ),
  tuning=list(
    "beta"=0.5, "phi"=0.5, "sigma.sq"=0.5, "w"=0.5
  ),
  priors=list(
    "beta.Normal"=list(0,1),
    "phi.unif"=c(3/0.5, 3/0.01),
    "sigma.sq.ig"=c(2, 1)
  ),
  n_batch = 100,
  batch_len = 100,
  verbose = FALSE
)

Model diagnostics

plot(m)

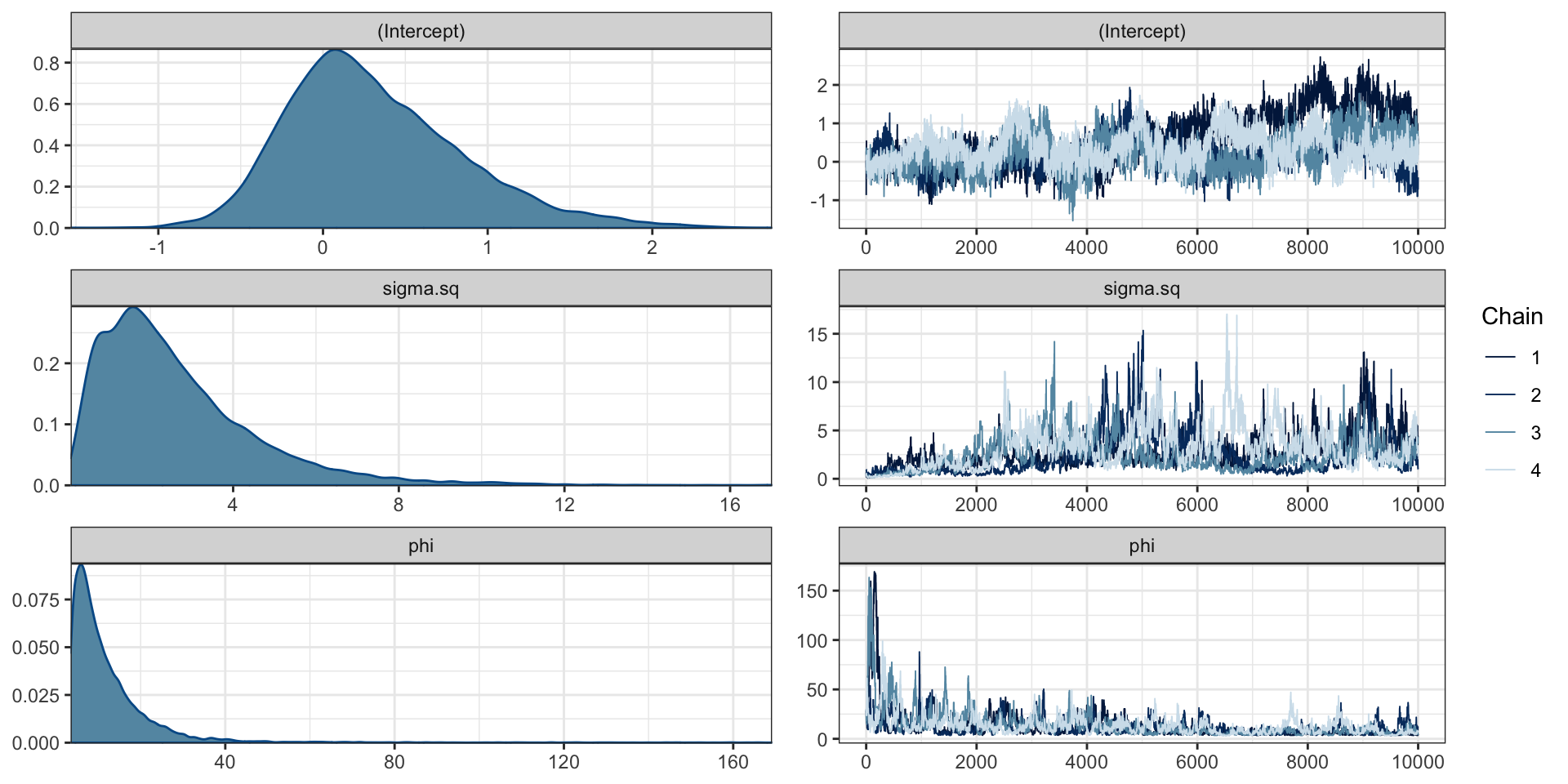
Model predictions

newdata = data.frame(
  x=seq(0,1,length.out=101)
)

(p = predict(m, newdata=newdata, coords="x", thin=50))

# A draws_matrix: 200 iterations, 4 chains, and 202 variables
    variable
draw  w[1]     w[2]   w[3]   w[4]   w[5]   w[6]  w[7]
  1  -1.18 -0.22201 -0.354  0.072  0.380 -0.226 -0.45
  2  -0.22 -0.00092 -0.167 -0.079  0.170  0.149 -0.29
  3  -0.64  0.09967 -0.345  0.357 -0.801 -0.339 -0.44
  4  -0.82  1.25431 -0.542 -1.391 -0.637 -0.033 -0.30
  5   0.19 -0.90628 -0.969 -0.561 -0.188 -1.444 -0.94
  6  -0.58 -1.01544  0.036 -0.611 -1.297 -1.107 -0.77
  7  -1.74  0.64735  0.036 -0.357 -1.268 -0.870 -0.70
  8  -0.25 -0.01433 -0.460  0.312 -0.046 -0.902 -1.68
  9  -0.83 -2.72657 -2.128 -1.316 -1.648 -2.682 -2.54
  10 -0.51 -1.15691 -1.570 -0.998 -1.074 -1.079 -1.63
    variable
draw   w[8]
  1  -0.042
  2  -0.671
  3  -0.440
  4  -0.368
  5  -0.346
  6  -0.706
  7   0.220
  8  -0.666
  9  -1.486
  10 -1.311
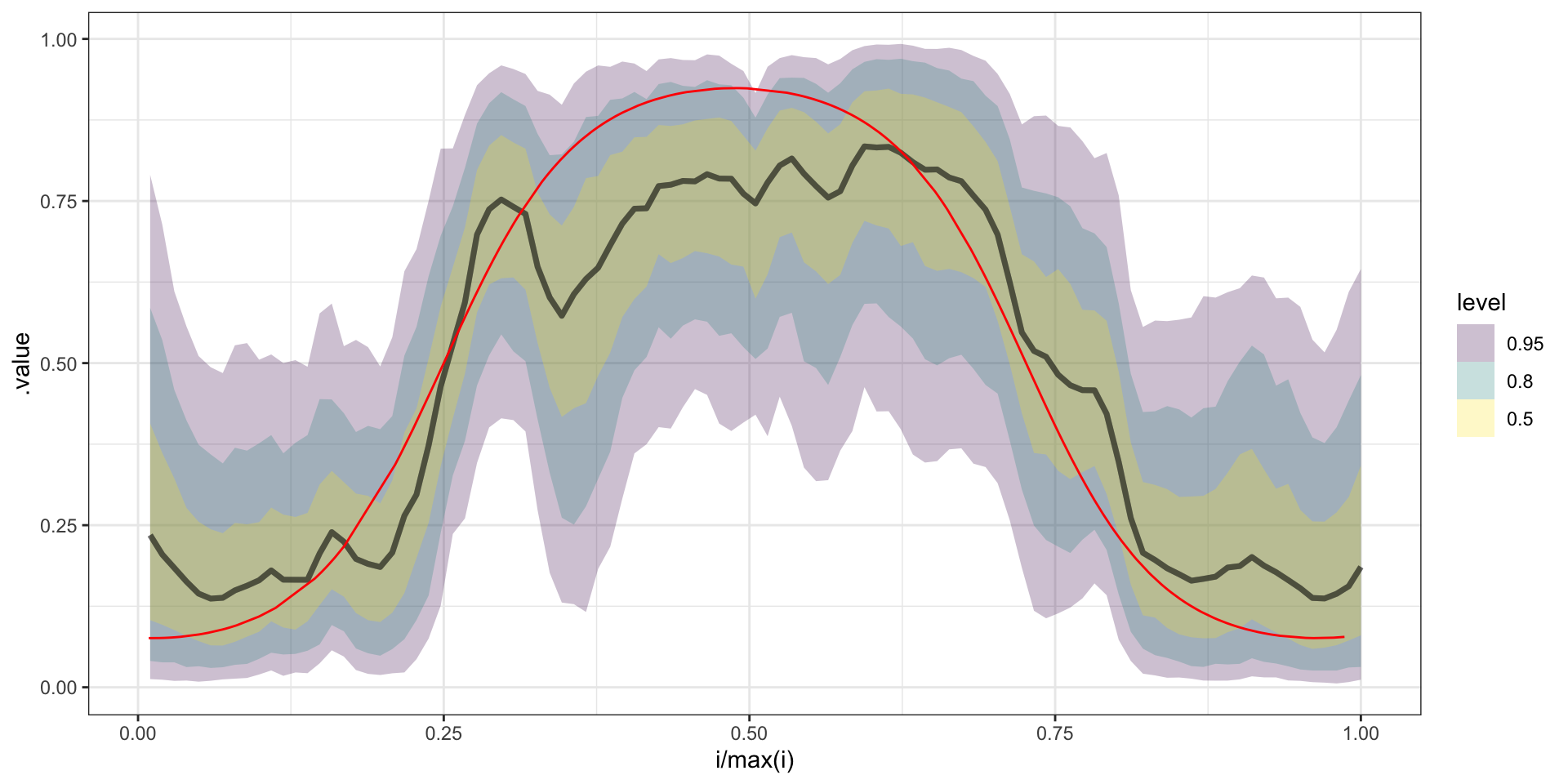
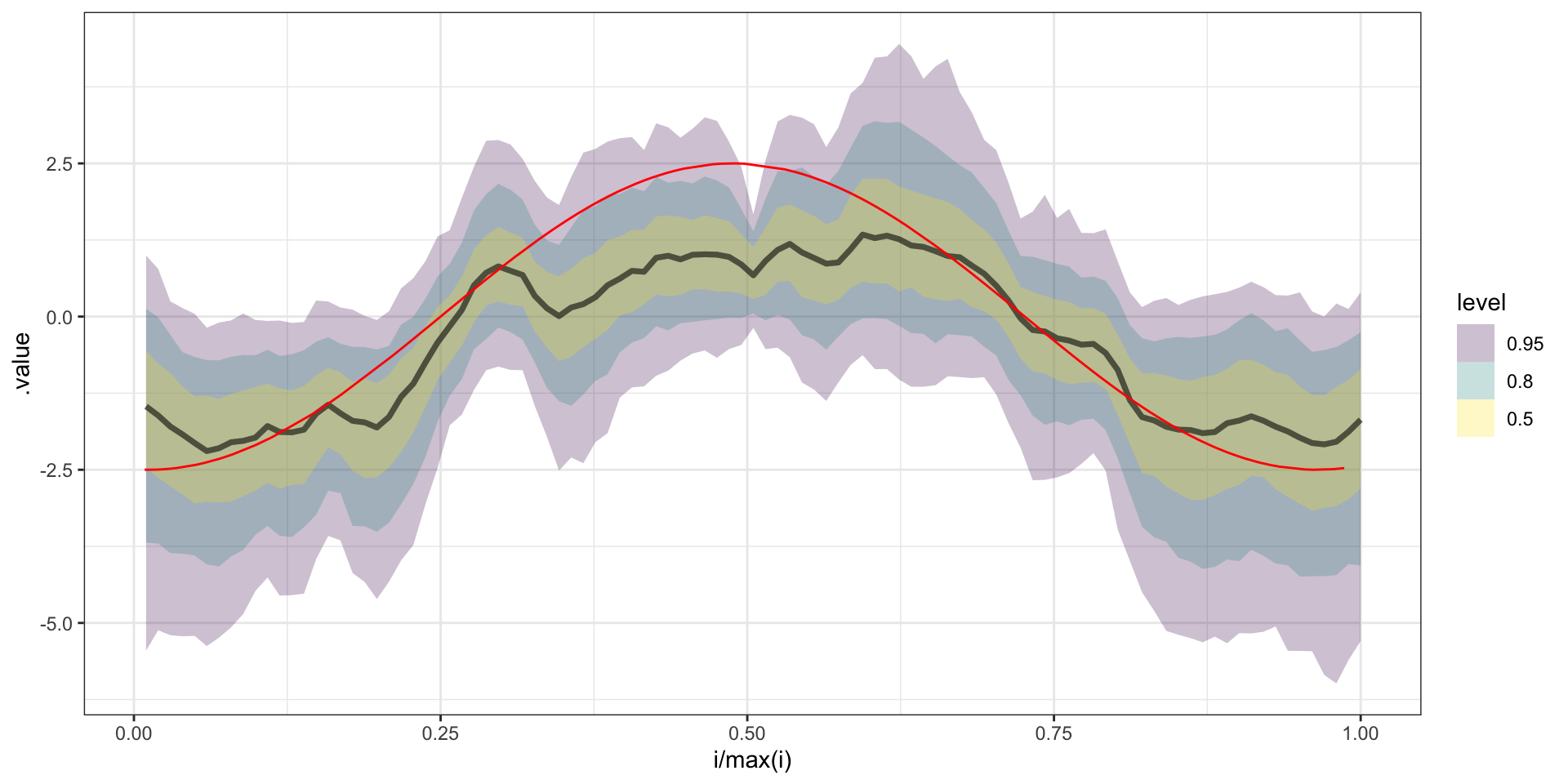
# ... with 790 more draws, and 194 more variables

Predicted y

p |>
  tidybayes::gather_draws(y[i]) |>
  ggplot2::ggplot(ggplot2::aes(x=i/max(i),y=.value)) +
    tidybayes::stat_lineribbon(alpha=0.25) +
    geom_line(data=d |> arrange(x), aes(x=x, y=p), color='red')

Predicted w

p |>
  tidybayes::gather_draws(w[i]) |>
  ggplot2::ggplot(ggplot2::aes(x=i/max(i),y=.value)) +
    tidybayes::stat_lineribbon(alpha=0.25) +
    geom_line(data=d |> arrange(x), aes(x=x, y=eta), color='red')

glm

g = glm(y~poly(x,2), data=d, family="binomial")

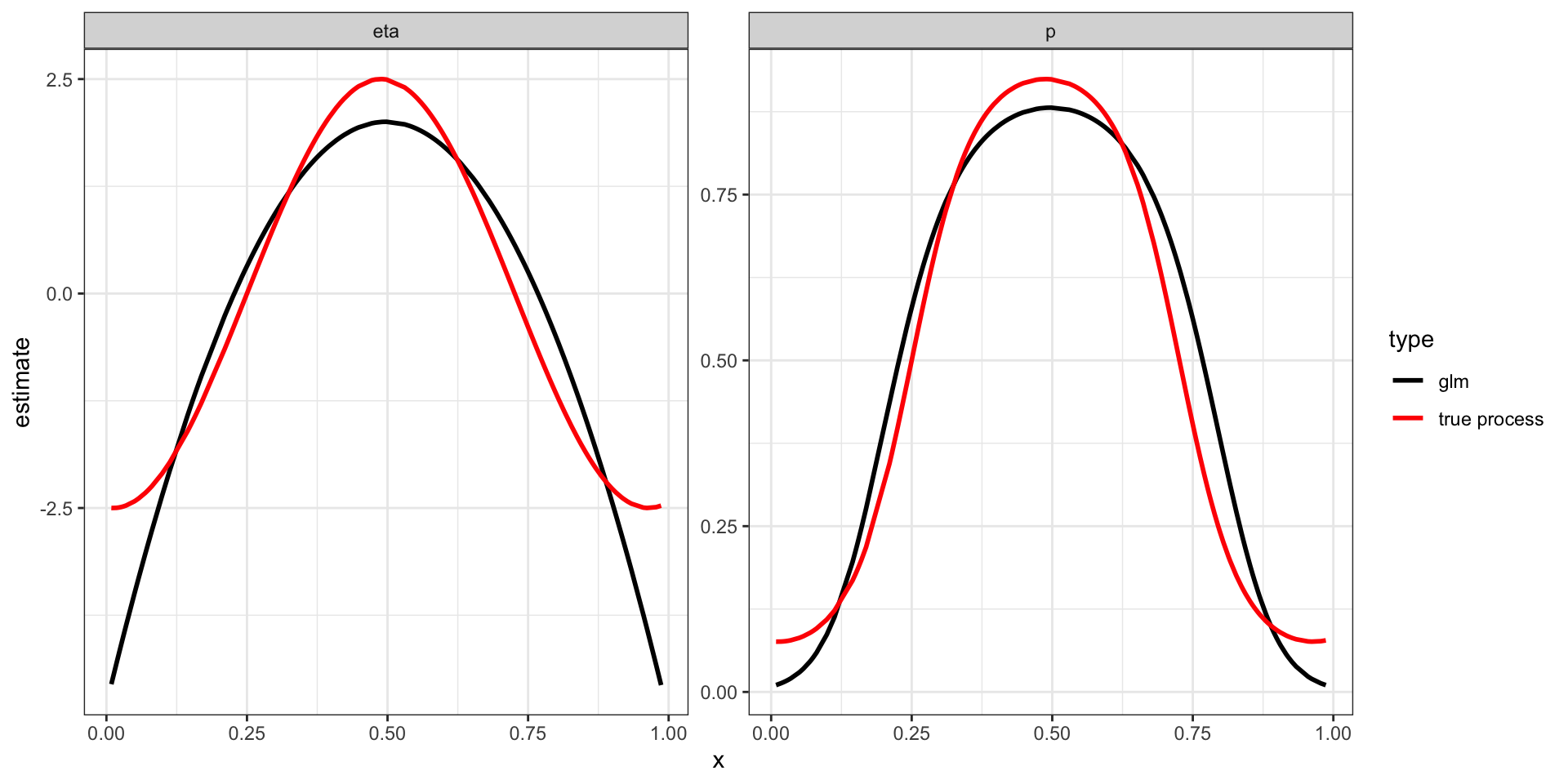
Count data

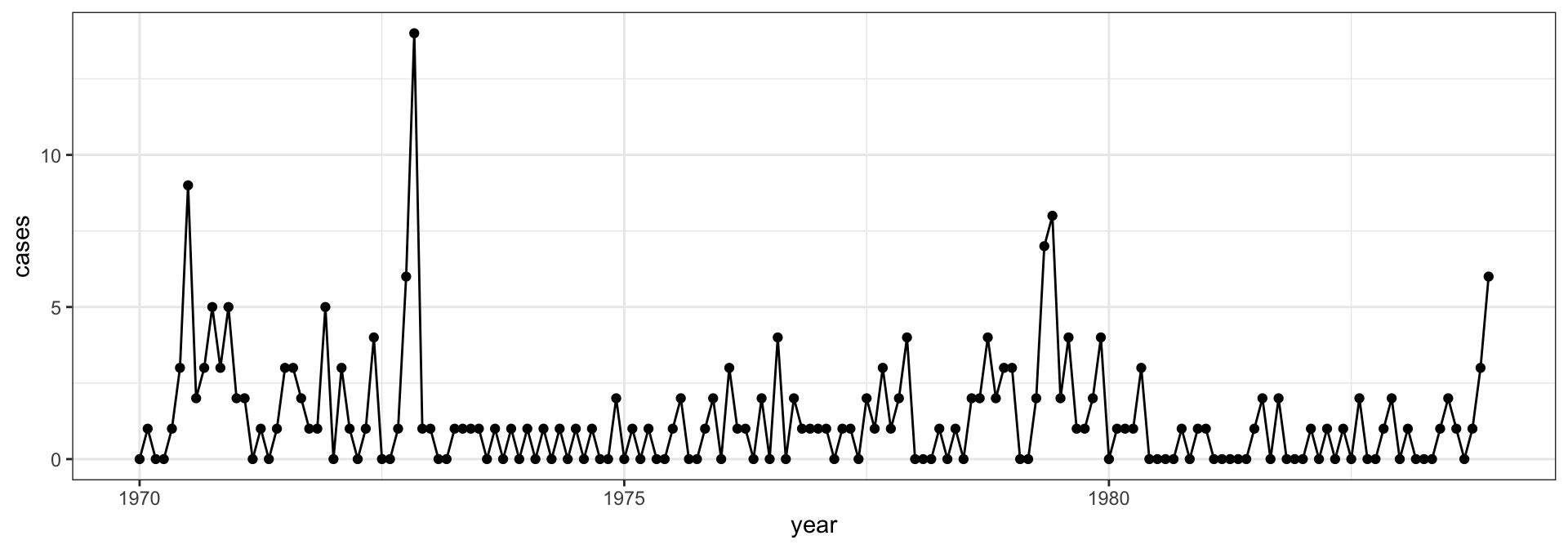
Polio cases

Polio from the glarma package.

This data set gives the monthly number of cases of poliomyelitis in the U.S. for the years 1970–1983 as reported by the Center for Disease Control.

Polio Model

Model: \[ \begin{aligned} y_i &\sim \text{Pois}(\lambda_i) \\ \text{log}(\lambda_i) &= \beta_0 + w(\boldsymbol{t}) \\ \\ w(\boldsymbol{t}) &\sim N(0,\Sigma) \\ \{\boldsymbol{\Sigma}\}_{ij} &= \sigma^2 \exp(-| l \, d_{ij}|) \end{aligned} \] . . .

Priors:

\[ \begin{aligned} \beta_0 &\sim N(0,1) \\ \phi &\sim \text{Unif}\left(\frac{3}{6}, \frac{3}{1/12}\right)\\ \sigma^2 &\sim \text{Inv-Gamma}(2,1) \end{aligned} \]

Model fitting

m = gpglm(
  cases~1, family="poisson",
  data = polio, coords = c("year"),
  cov_model = "exponential",
  starting=list(
    "beta"=0, "phi"=3/2, "sigma.sq"=1, "w"=0
  ),
  tuning=list(
    "beta"=0.5, "phi"=0.5, "sigma.sq"=0.5, "w"=0.5
  ),
  priors=list(
    "beta.Normal"=list(0,1),
    "phi.unif"=c(3/6, 3/(1/12)),
    "sigma.sq.ig"=c(2, 1)
  ),
  n_batch = 100,
  batch_len = 100,
  verbose = FALSE
)

Model diagnostics

plot(m)

Model fit

newdata = data.frame(
  year = seq(1970, 1984, by=0.1) |> jitter()
)

(p = predict(m, newdata=newdata, coords="year", thin=50))

# A draws_matrix: 200 iterations, 4 chains, and 282 variables
    variable
draw   w[1]   w[2]    w[3]    w[4]  w[5] w[6]    w[7]  w[8]
  1  -0.498  0.065  0.3183  0.2519 -0.52 0.32 -0.0085 -0.22
  2   0.190 -0.115 -0.0028  0.0917  1.12 1.62  1.0786  1.34
  3  -1.322 -0.651 -0.5380 -0.4450  0.94 1.80  1.5415  1.80
  4   0.112  0.075  0.3479  0.6895  1.05 1.68  1.6113  0.79
  5  -0.043 -0.088 -0.2408 -0.2396  2.15 1.79 -0.0989  1.04
  6  -0.528 -0.995 -0.9240 -0.0067  1.50 2.00  0.9907  1.63
  7  -1.779 -0.426 -1.2744  0.9432  0.51 0.90  1.2267  0.04
  8  -0.594 -0.119 -0.9112 -0.0822  1.69 1.28  0.2578  0.88
  9   0.259  0.157  0.3803  0.4777  0.30 1.23  0.3618  0.35
  10 -1.880 -1.996 -0.5955 -0.5550  1.45 1.43  0.6164  0.61
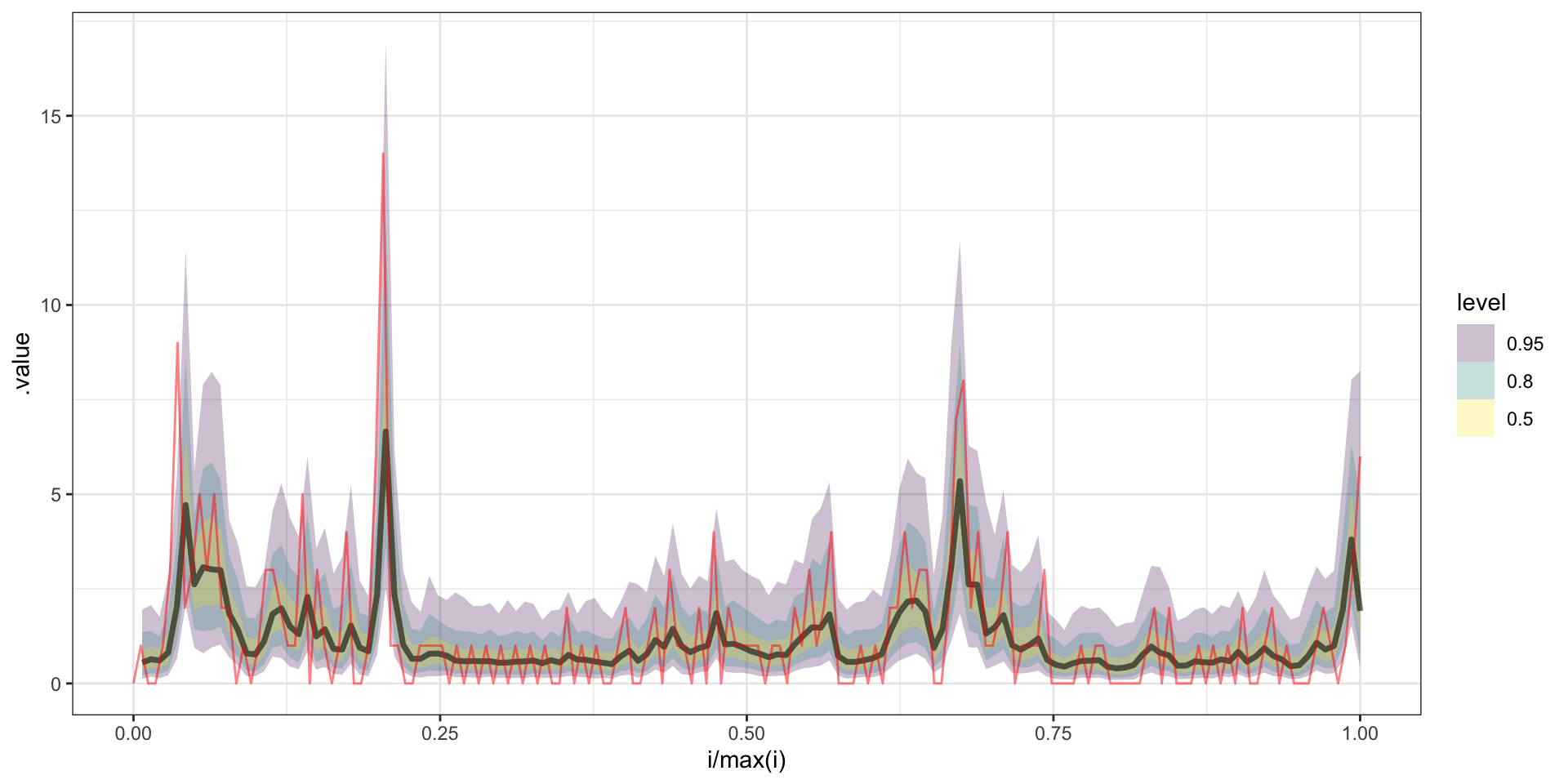
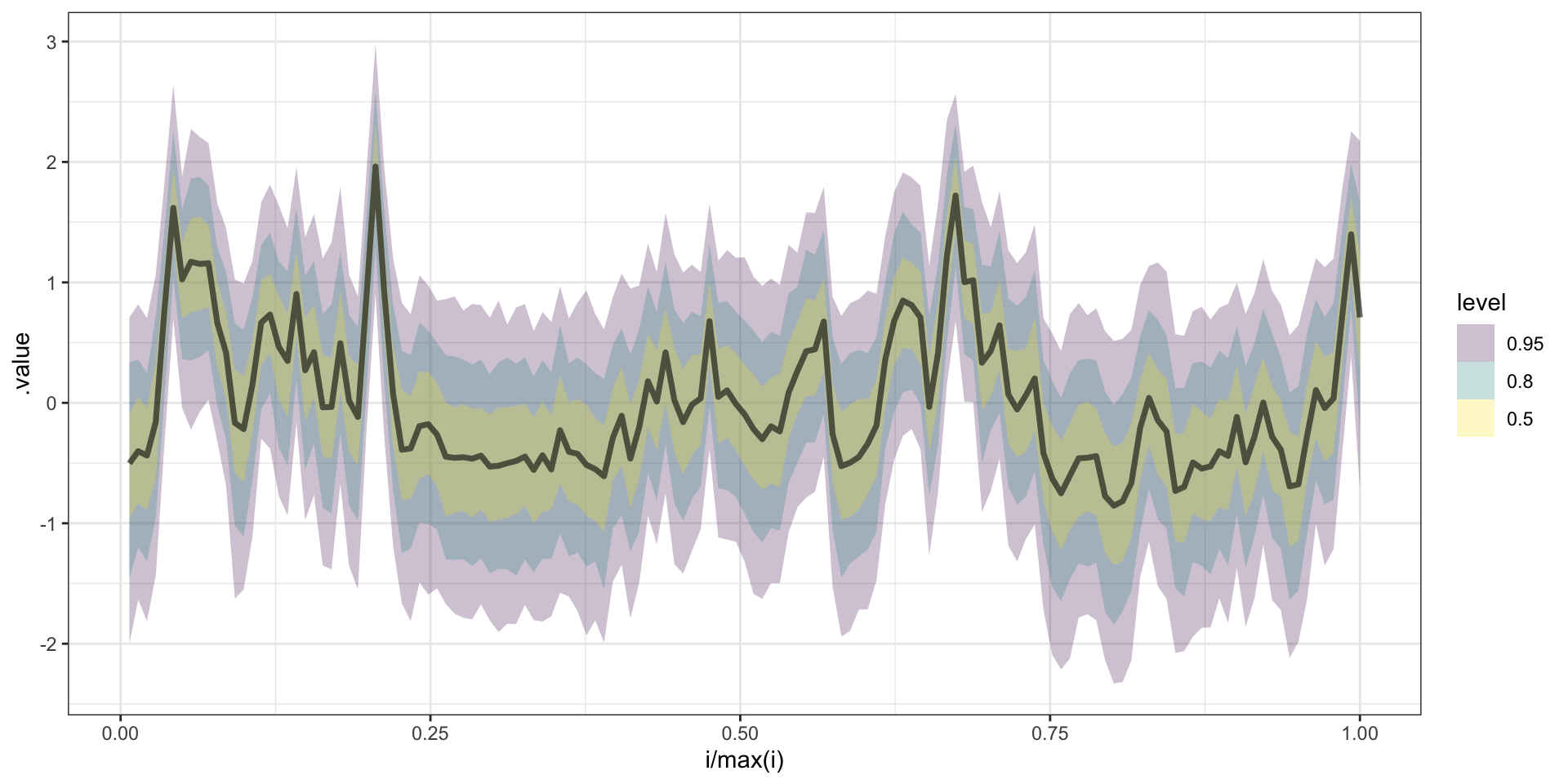
# ... with 790 more draws, and 274 more variables

Predicted y

p |>
  tidybayes::gather_draws(y[i]) |>
  ggplot2::ggplot(ggplot2::aes(x=i/max(i),y=.value)) +
    tidybayes::stat_lineribbon(alpha=0.25) +
    geom_line(data=polio, aes(x=(year-min(year))/(max(year)-min(year)), y=cases), color='red', alpha=0.5)

Predicted w

p |>
  tidybayes::gather_draws(w[i]) |>
  ggplot2::ggplot(ggplot2::aes(x=i/max(i),y=.value)) +
    tidybayes::stat_lineribbon(alpha=0.25)

Spatial data in R

Packages for geospatial data in R

R has a rich package ecosystem for read/writing, manipulating, and analyzing geospatial data.

Some core packages:

sp - core classes for handling spatial data, additional utility functions - Deprecated
rgdal - R interface to gdal (Geospatial Data Abstraction Library) for reading and writing spatial data - Deprecated
rgeos - R interface to geos (Geometry Engine Open Source) library for querying and manipulating spatial data. Reading and writing WKT. - Deprecated
sf - Combines the functionality of sp, rgdal, and rgeos into a single package based on tidy simple features.
raster - classes and tools for handling spatial raster data.
stars - Reading, manipulating, writing and plotting spatiotemporal arrays (rasters)

See more - Spatial task view

Installing `sf`

This is the hardest part of using the sf package, difficulty comes from is dependence on several external libraries (geos, gdal, and proj).

Windows - installing from source works when Rtools is installed (system requirements are downloaded from rwinlib)
MacOS - install dependencies via homebrew: gdal2, geos, proj.
Linux - Install development packages for GDAL (>= 2.0.0), GEOS (>= 3.3.0) and Proj.4 (>= 4.8.0) from your package manager of choice.

More specific details are included in the README on github.

Simple Features

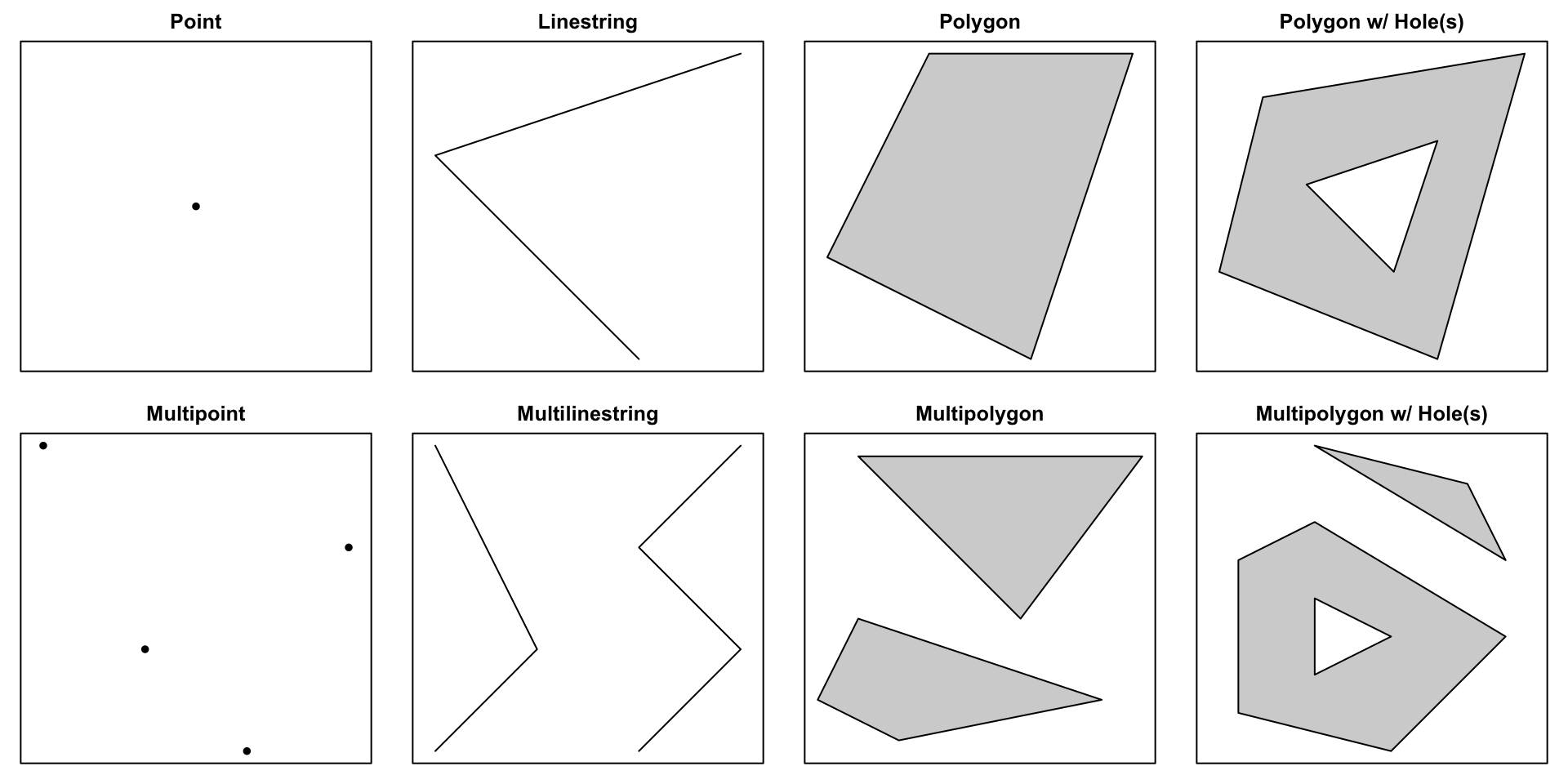
Reading, writing, and converting

sf
- st_read() / st_write() - Shapefile, GeoJSON, KML, …
- read_sf() / write_sf() - Same, supports tibbles …
- st_as_sfc() / st_as_wkt() - sf <-> WKT
- st_as_sfc() / st_as_binary() - sf <-> WKB
- st_as_sfc() / as(x, "Spatial") - sf <-> sp

Geospatial data in
the real world

Projections

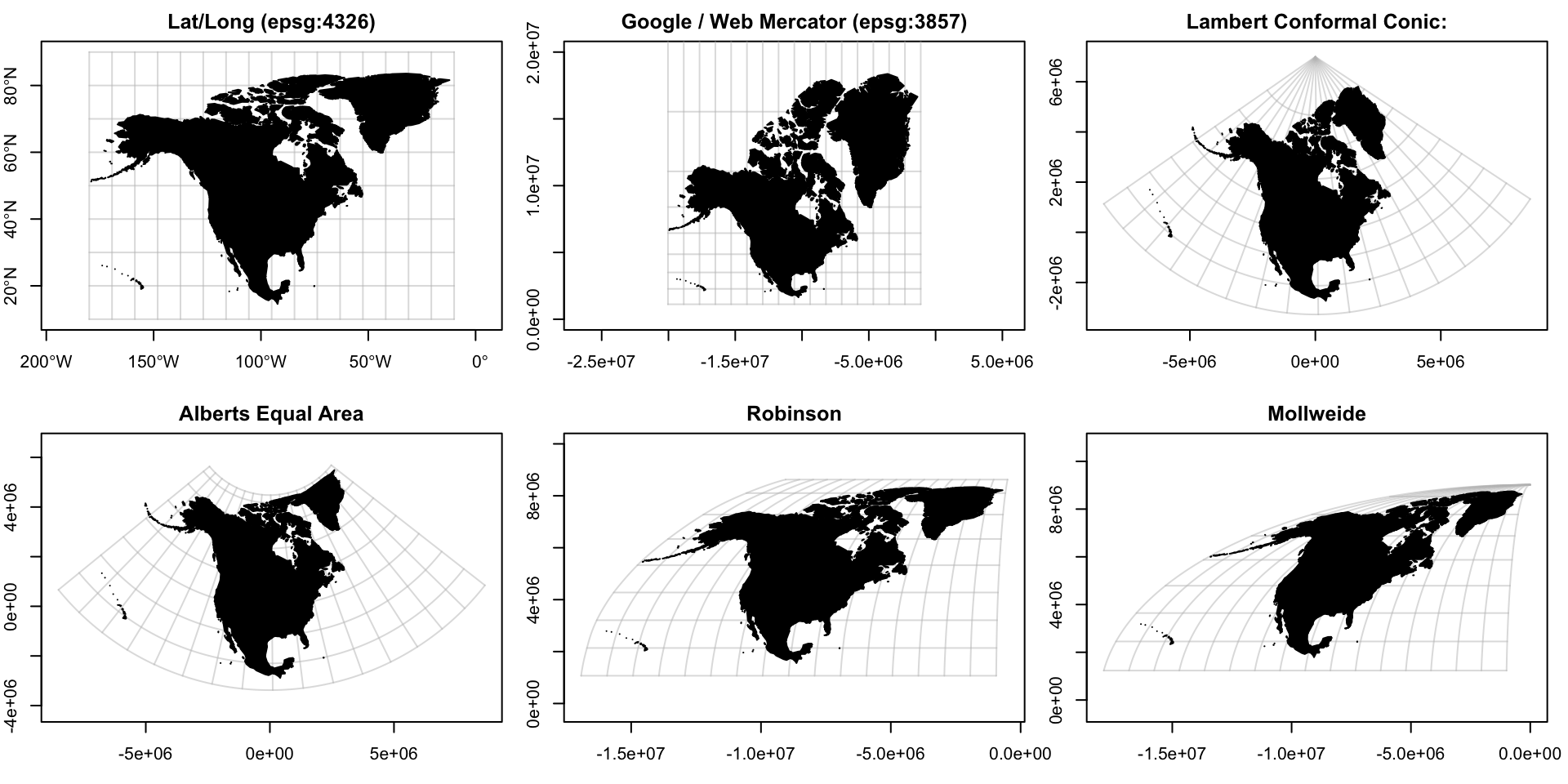
Distance on a Sphere

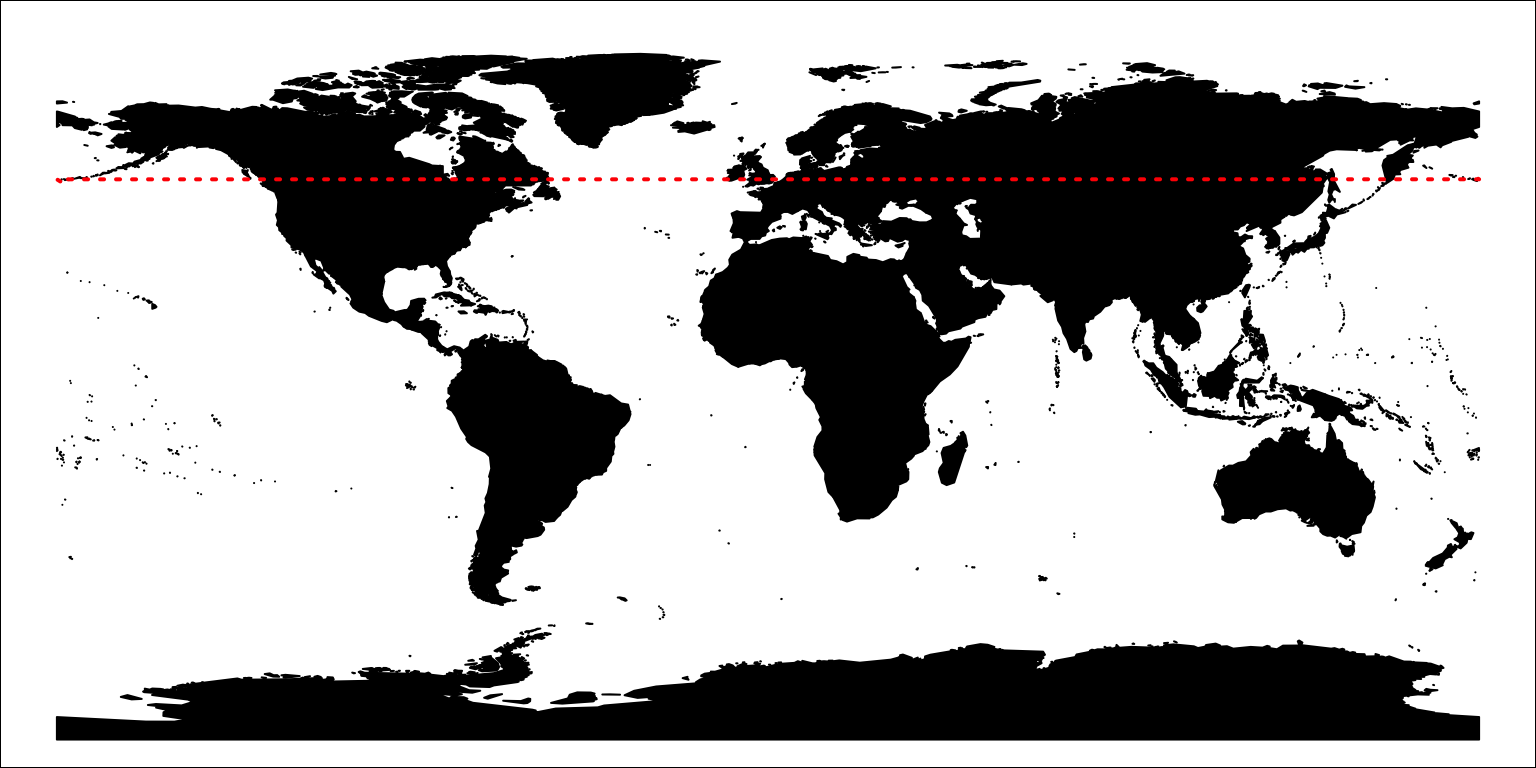
Dateline

How long is the flight between the Western most and the Eastern most points in the US?

path = geosphere::gcIntermediate(
  c(179.776, 51.952), c(-179.146, 51.273), 
  n=50, addStartEnd=TRUE
)

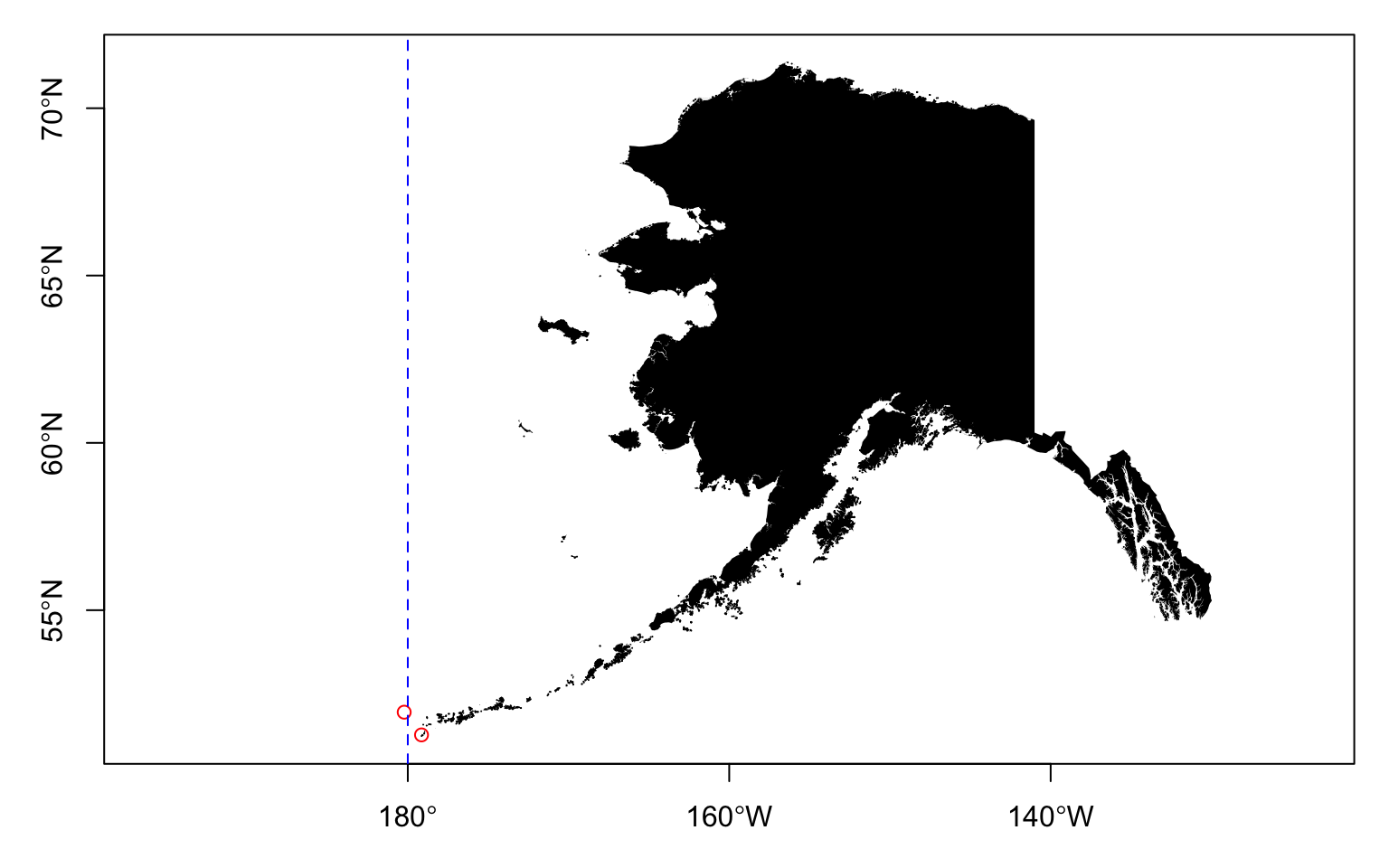
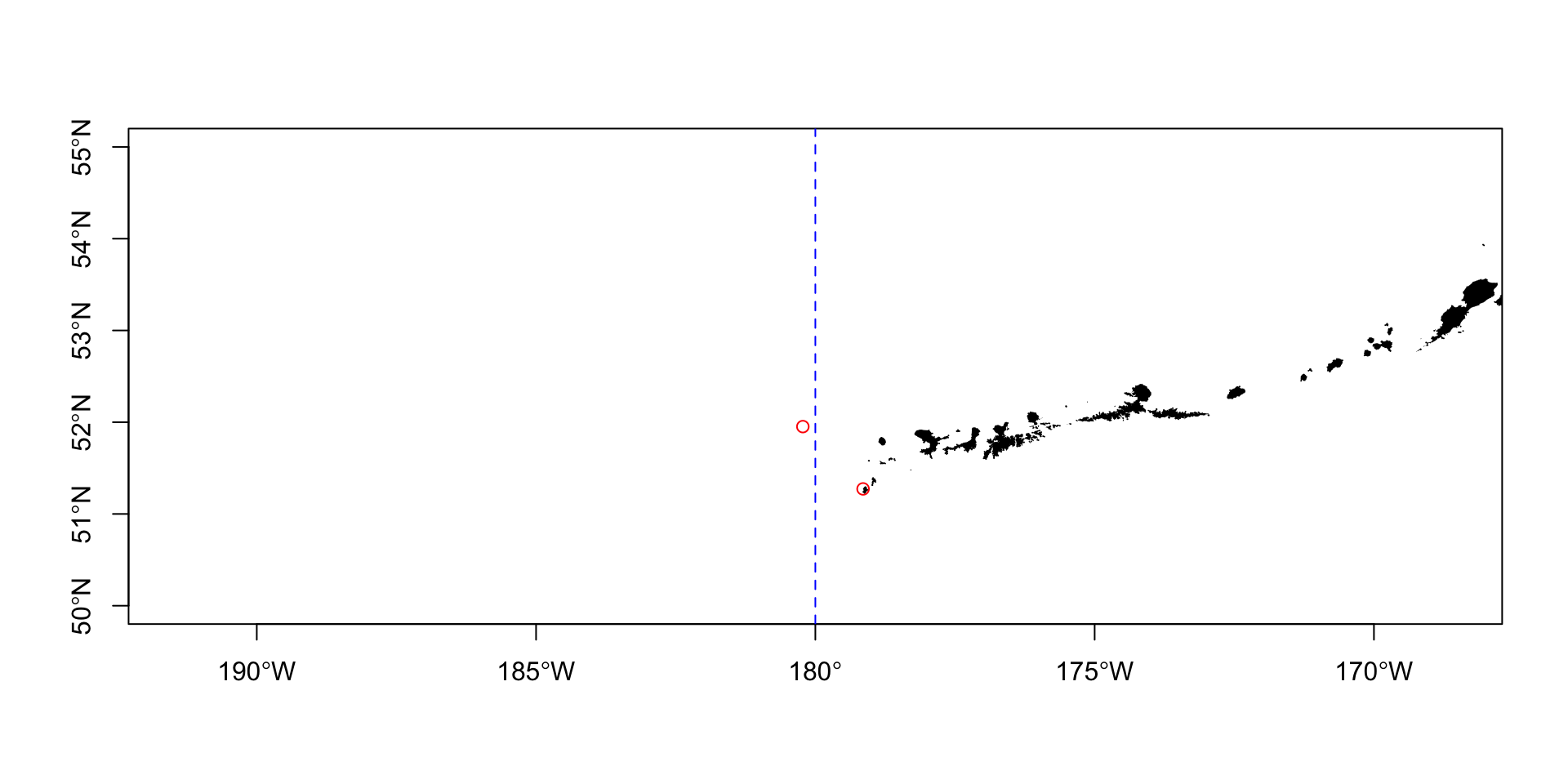
Using `sf`

Example data

nc  = read_sf("data/gis/nc_counties/", quiet=TRUE)
air = read_sf("data/gis/airports/", quiet=TRUE)
hwy = read_sf("data/gis/us_interstates/", quiet=TRUE)

nc

Simple feature collection with 100 features and 8 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: -84.32186 ymin: 33.84175 xmax: -75.46003 ymax: 36.58815
Geodetic CRS:  NAD83
# A tibble: 100 × 9
     AREA PERIM…¹ COUNT…² STATE COUNTY FIPS  STATE…³ SQUAR…⁴
    <dbl>   <dbl>   <dbl> <chr> <chr>  <chr> <chr>     <dbl>
 1 0.112     1.61    1994 NC    Ashe … 37009 37         429.
 2 0.0616    1.35    1996 NC    Alleg… 37005 37         236.
 3 0.140     1.77    1998 NC    Surry… 37171 37         539.
 4 0.0891    1.43    1999 NC    Gates… 37073 37         342.
 5 0.0687    4.43    2000 NC    Curri… 37053 37         264.
 6 0.119     1.40    2001 NC    Stoke… 37169 37         456.
 7 0.0626    2.11    2002 NC    Camde… 37029 37         241.
 8 0.115     1.46    2003 NC    Warre… 37185 37         444.
 9 0.143     2.40    2004 NC    North… 37131 37         551.
10 0.0925    1.81    2005 NC    Hertf… 37091 37         356.
# … with 90 more rows, 1 more variable:
#   geometry <MULTIPOLYGON [°]>, and abbreviated variable
#   names ¹PERIMETER, ²COUNTYP010, ³STATE_FIPS, ⁴SQUARE_MIL

air

Simple feature collection with 940 features and 16 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -176.646 ymin: 17.70156 xmax: -64.80172 ymax: 71.28545
Geodetic CRS:  NAD83
# A tibble: 940 × 17
   AIRPRTX…¹ FEATURE ICAO  IATA  AIRPT…² CITY  STATE STATE…³
       <dbl> <chr>   <chr> <chr> <chr>   <chr> <chr> <chr>  
 1         0 AIRPORT KGON  GON   GROTON… GROT… CT    09     
 2         3 AIRPORT K6S5  6S5   RAVALL… HAMI… MT    30     
 3         4 AIRPORT KMHV  MHV   MOJAVE… MOJA… CA    06     
 4         6 AIRPORT KSEE  SEE   GILLES… SAN … CA    06     
 5         7 AIRPORT KFPR  FPR   ST LUC… FORT… FL    12     
 6         8 AIRPORT KRYY  RYY   COBB C… ATLA… GA    13     
 7        10 AIRPORT KMKL  MKL   MC KEL… JACK… TN    47     
 8        11 AIRPORT KCCR  CCR   BUCHAN… CONC… CA    06     
 9        13 AIRPORT KJYO  JYO   LEESBU… LEES… VA    51     
10        15 AIRPORT KCAD  CAD   WEXFOR… CADI… MI    26     
# … with 930 more rows, 9 more variables: COUNTY <chr>,
#   FIPS <chr>, TOT_ENP <dbl>, LATITUDE <dbl>,
#   LONGITUDE <dbl>, ELEV <dbl>, ACT_DATE <chr>,
#   CNTL_TWR <chr>, geometry <POINT [°]>, and abbreviated
#   variable names ¹AIRPRTX010, ²AIRPT_NAME, ³STATE_FIPS

hwy

Simple feature collection with 233 features and 3 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: -7472582 ymin: 2911107 xmax: 2443707 ymax: 8208428
Projected CRS: NAD83 / UTM zone 15N
# A tibble: 233 × 4
   ROUTE_NUM DIST_MILES DIST_KM                     geometry
   <chr>          <dbl>   <dbl>        <MULTILINESTRING [m]>
 1 I10          2449.   3941.   ((-1881200 4072307, -187992…
 2 I105           20.8    33.4  ((-1910156 5339585, -191013…
 3 I110           41.4    66.6  ((1054139 3388879, 1054287 …
 4 I115            1.58    2.55 ((-1013796 5284243, -101313…
 5 I12            85.3   137.   ((680741.7 3366581, 682709.…
 6 I124            1.73    2.79 ((1201467 3906285, 1201643 …
 7 I126            3.56    5.72 ((1601502 3829718, 1602136 …
 8 I129            3.1     4.99 ((217446 4705389, 217835.1 …
 9 I135           96.3   155.   ((96922.97 4313125, 96561.8…
10 I15          1436.   2311    ((-882875.7 5602902, -88299…
# … with 223 more rows

`sf` structure

str(nc)

sf [100 × 9] (S3: sf/tbl_df/tbl/data.frame)
 $ AREA      : num [1:100] 0.1118 0.0616 0.1402 0.0891 0.0687 ...
 $ PERIMETER : num [1:100] 1.61 1.35 1.77 1.43 4.43 ...
 $ COUNTYP010: num [1:100] 1994 1996 1998 1999 2000 ...
 $ STATE     : chr [1:100] "NC" "NC" "NC" "NC" ...
 $ COUNTY    : chr [1:100] "Ashe County" "Alleghany County" "Surry County" "Gates County" ...
 $ FIPS      : chr [1:100] "37009" "37005" "37171" "37073" ...
 $ STATE_FIPS: chr [1:100] "37" "37" "37" "37" ...
 $ SQUARE_MIL: num [1:100] 429 236 539 342 264 ...
 $ geometry  :sfc_MULTIPOLYGON of length 100; first list element: List of 1
  ..$ :List of 1
  .. ..$ : num [1:1030, 1:2] -81.7 -81.7 -81.7 -81.6 -81.6 ...
  ..- attr(*, "class")= chr [1:3] "XY" "MULTIPOLYGON" "sfg"
 - attr(*, "sf_column")= chr "geometry"
 - attr(*, "agr")= Factor w/ 3 levels "constant","aggregate",..: NA NA NA NA NA NA NA NA
  ..- attr(*, "names")= chr [1:8] "AREA" "PERIMETER" "COUNTYP010" "STATE" ...

`sf` classes

class(nc)

[1] "sf"         "tbl_df"     "tbl"        "data.frame"

class(nc$geometry)

[1] "sfc_MULTIPOLYGON" "sfc"

class(nc$geometry[[1]])

[1] "XY"           "MULTIPOLYGON" "sfg"

Projections

st_crs(nc)

Coordinate Reference System:
  User input: NAD83 
  wkt:
GEOGCRS["NAD83",
    DATUM["North American Datum 1983",
        ELLIPSOID["GRS 1980",6378137,298.257222101,
            LENGTHUNIT["metre",1]]],
    PRIMEM["Greenwich",0,
        ANGLEUNIT["degree",0.0174532925199433]],
    CS[ellipsoidal,2],
        AXIS["latitude",north,
            ORDER[1],
            ANGLEUNIT["degree",0.0174532925199433]],
        AXIS["longitude",east,
            ORDER[2],
            ANGLEUNIT["degree",0.0174532925199433]],
    ID["EPSG",4269]]

st_crs(hwy)

Coordinate Reference System:
  User input: NAD83 / UTM zone 15N 
  wkt:
PROJCRS["NAD83 / UTM zone 15N",
    BASEGEOGCRS["NAD83",
        DATUM["North American Datum 1983",
            ELLIPSOID["GRS 1980",6378137,298.257222101,
                LENGTHUNIT["metre",1]]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["degree",0.0174532925199433]],
        ID["EPSG",4269]],
    CONVERSION["UTM zone 15N",
        METHOD["Transverse Mercator",
            ID["EPSG",9807]],
        PARAMETER["Latitude of natural origin",0,
            ANGLEUNIT["Degree",0.0174532925199433],
            ID["EPSG",8801]],
        PARAMETER["Longitude of natural origin",-93,
            ANGLEUNIT["Degree",0.0174532925199433],
            ID["EPSG",8802]],
        PARAMETER["Scale factor at natural origin",0.9996,
            SCALEUNIT["unity",1],
            ID["EPSG",8805]],
        PARAMETER["False easting",500000,
            LENGTHUNIT["metre",1],
            ID["EPSG",8806]],
        PARAMETER["False northing",0,
            LENGTHUNIT["metre",1],
            ID["EPSG",8807]]],
    CS[Cartesian,2],
        AXIS["(E)",east,
            ORDER[1],
            LENGTHUNIT["metre",1]],
        AXIS["(N)",north,
            ORDER[2],
            LENGTHUNIT["metre",1]],
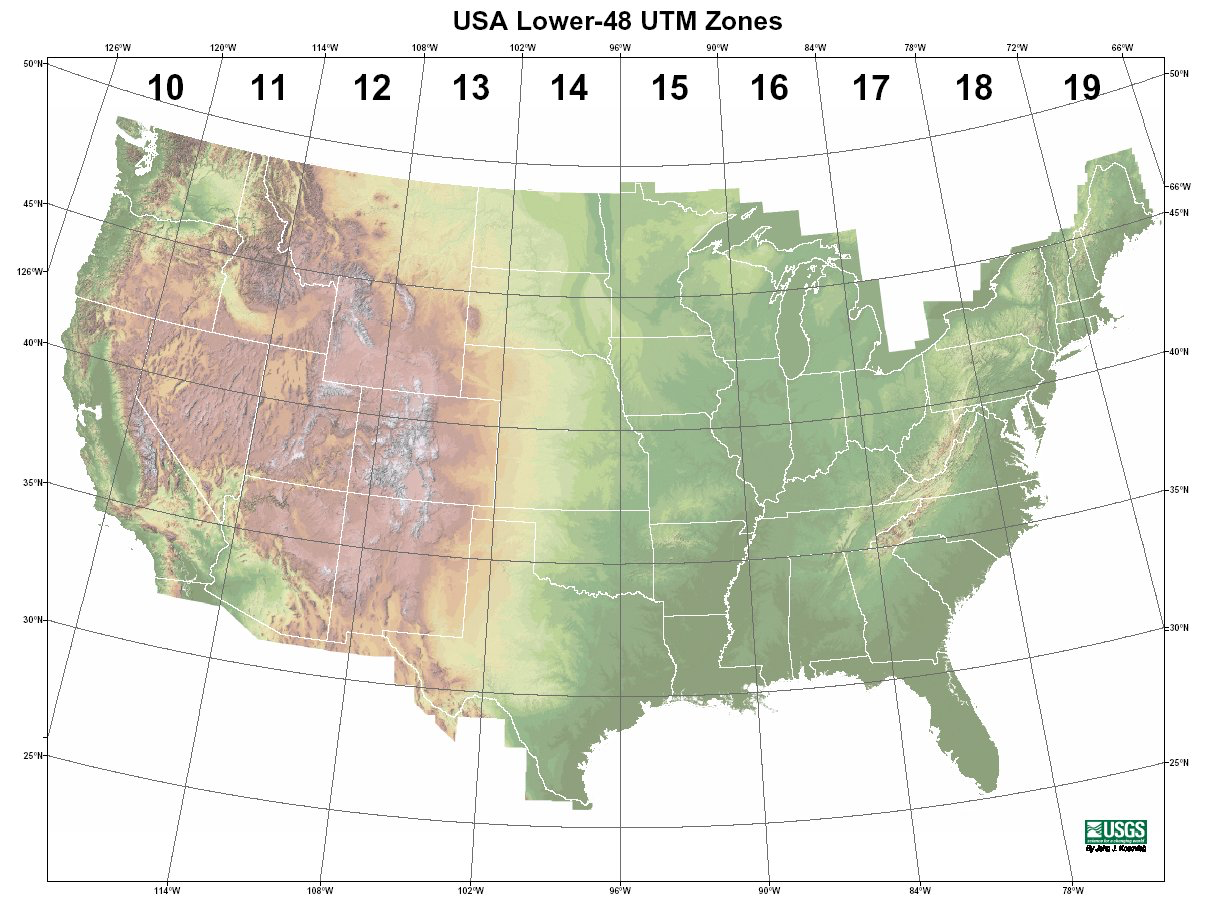
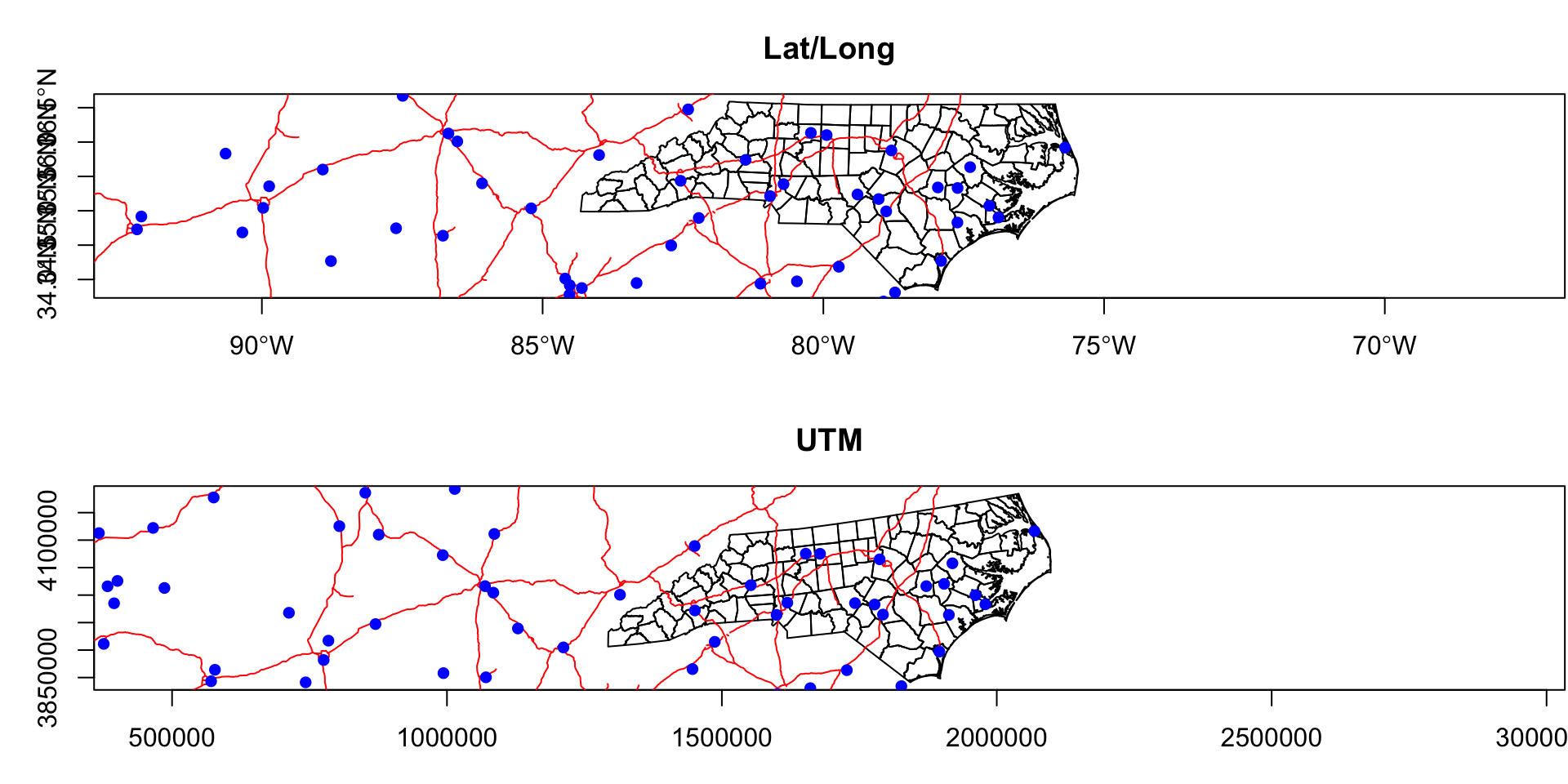
    ID["EPSG",26915]]

UTM Zones

Lat/Long

nc_ll = nc
air_ll = air
hwy_ll = st_transform(hwy, st_crs(nc))

UTM

nc_utm = st_transform(nc, st_crs(hwy))
air_utm = st_transform(air, st_crs(hwy))
hwy_utm = hwy

GPs for GLMs+ Spatial Data

GPs and GLMs

Logistic Regression

A toy example

Model fitting

Model diagnostics

Model predictions

Predicted y

Predicted w

glm

Count data

Polio cases

Polio Model

Model fitting

Model diagnostics

Model fit

Predicted y

Predicted w

Spatial data in R

Packages for geospatial data in R

Installing sf

Simple Features

Reading, writing, and converting

Geospatial data inthe real world

Projections

Distance on a Sphere

Dateline

Using sf

Example data

sf structure

sf classes

Projections

UTM Zones

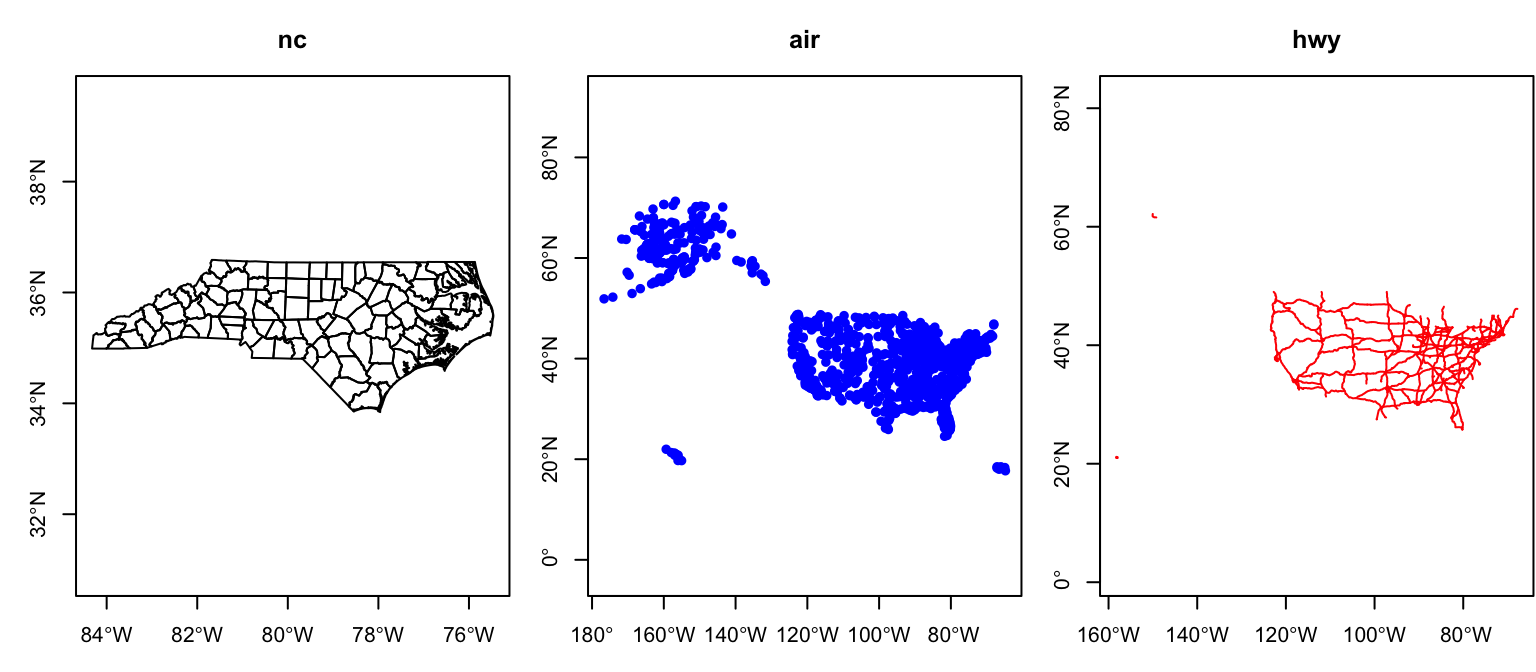
Lat/Long

UTM

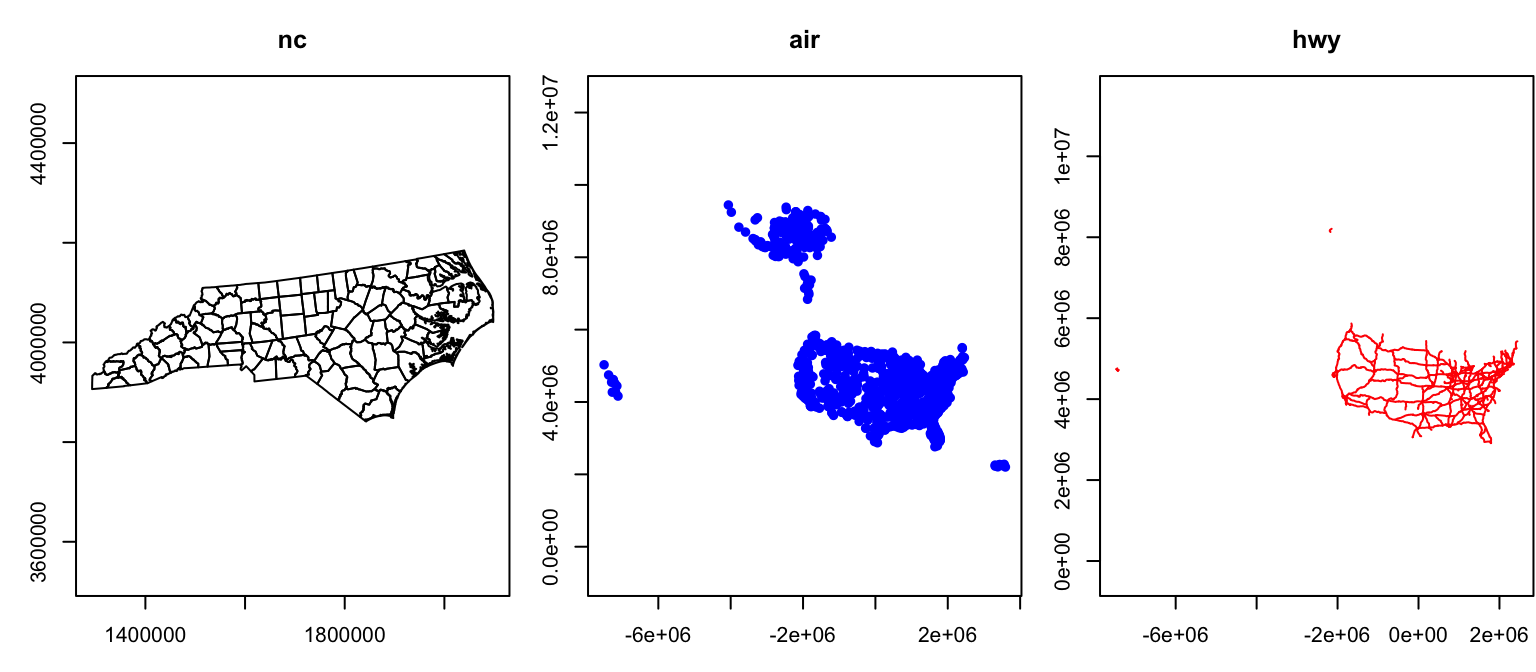
Comparison

GPs for GLMs
+ Spatial Data

Installing `sf`

Geospatial data in
the real world

Using `sf`

`sf` structure

`sf` classes