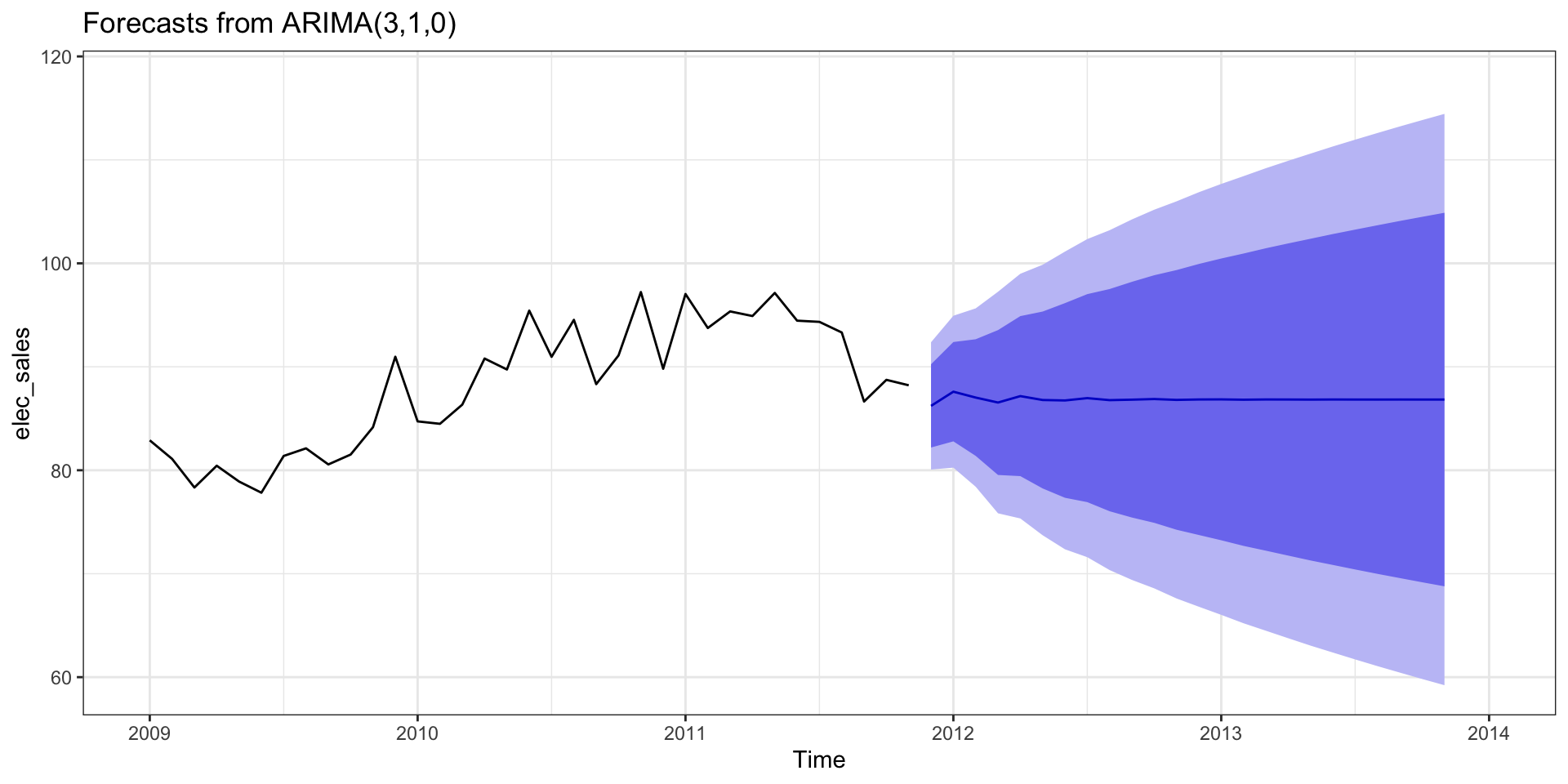
Series: elec_sales
ARIMA(3,1,0)
Coefficients:
ar1 ar2 ar3
-0.3488 -0.0386 0.3139
s.e. 0.0690 0.0736 0.0694
sigma^2 = 9.853: log likelihood = -485.67
AIC=979.33 AICc=979.55 BIC=992.32Seasonal Arima
Lecture 11
ARIMA - General Guidance
Positive autocorrelations out to a large number of lags usually indicates a need for differencing
Slightly too much or slightly too little differencing can be corrected by adding AR or MA terms respectively.
A model with no differencing usually includes a constant term, a model with two or more orders (rare) differencing usually does not include a constant term.
After differencing, if the PACF has a sharp cutoff then consider adding AR terms to the model.
After differencing, if the ACF has a sharp cutoff then consider adding an MA term to the model.
It is possible for an AR term and an MA term to cancel each other’s effects, so try models with fewer AR terms and fewer MA terms.
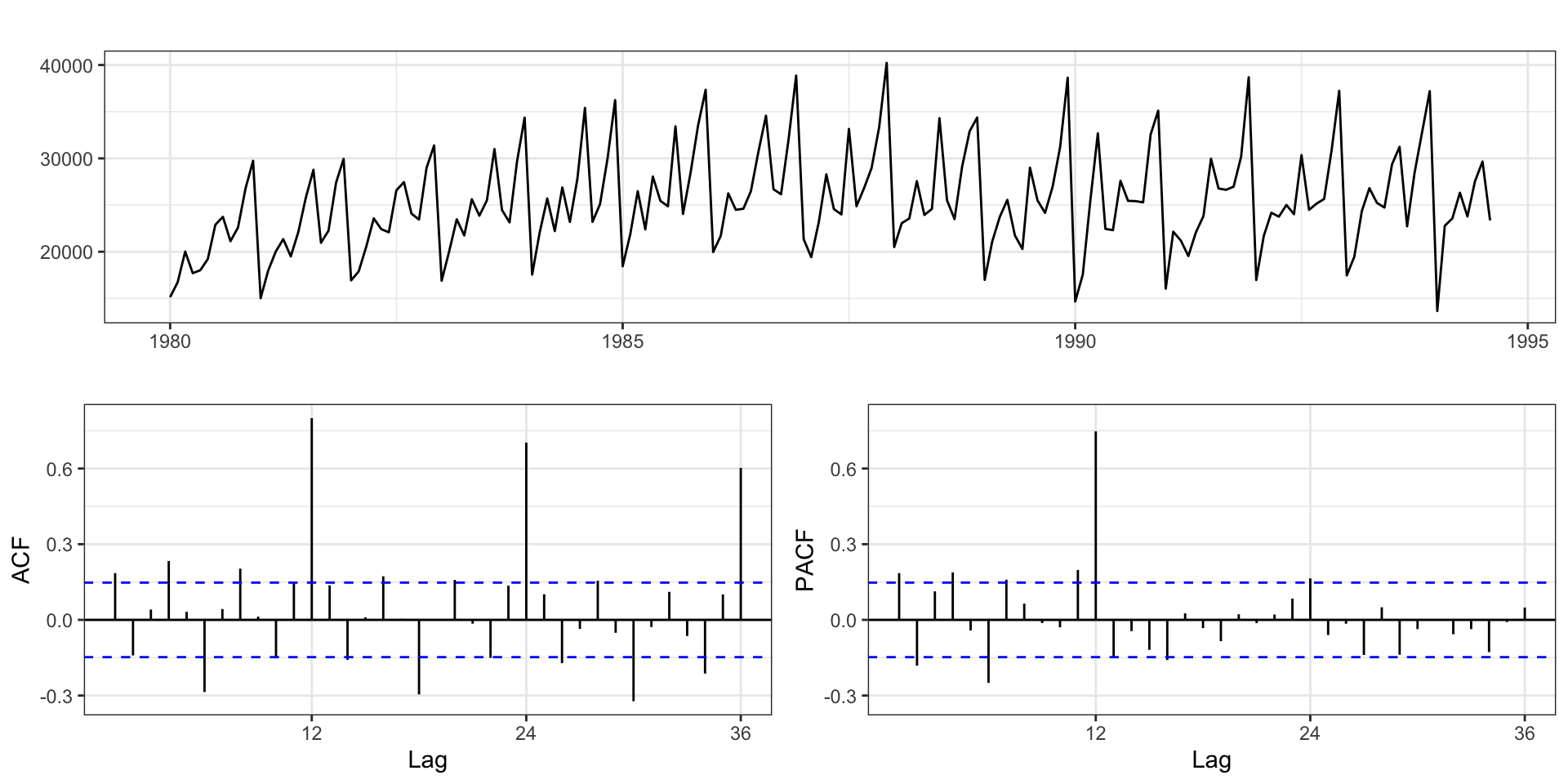
Electrical Equipment Sales
Data
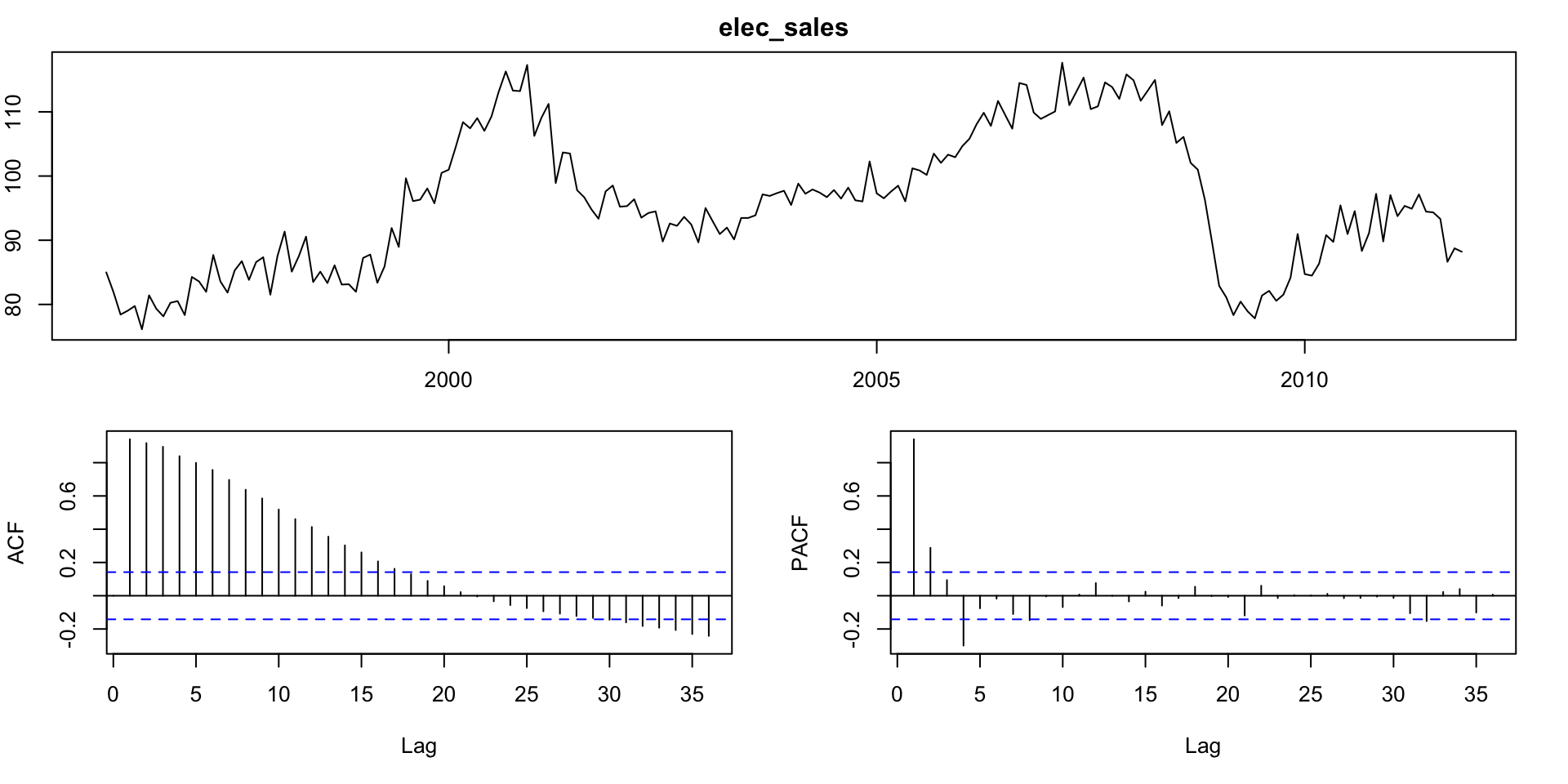
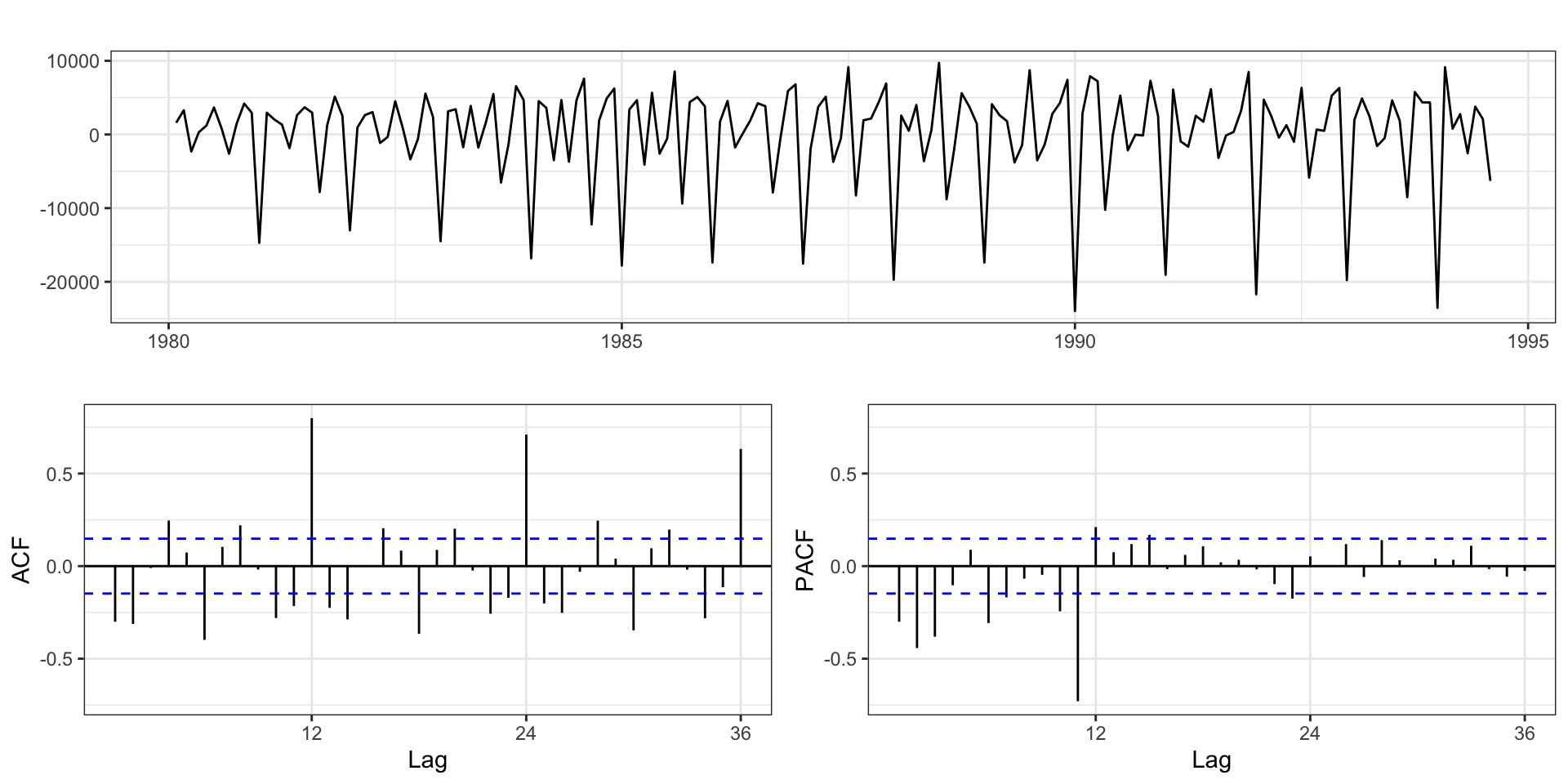
1st order differencing
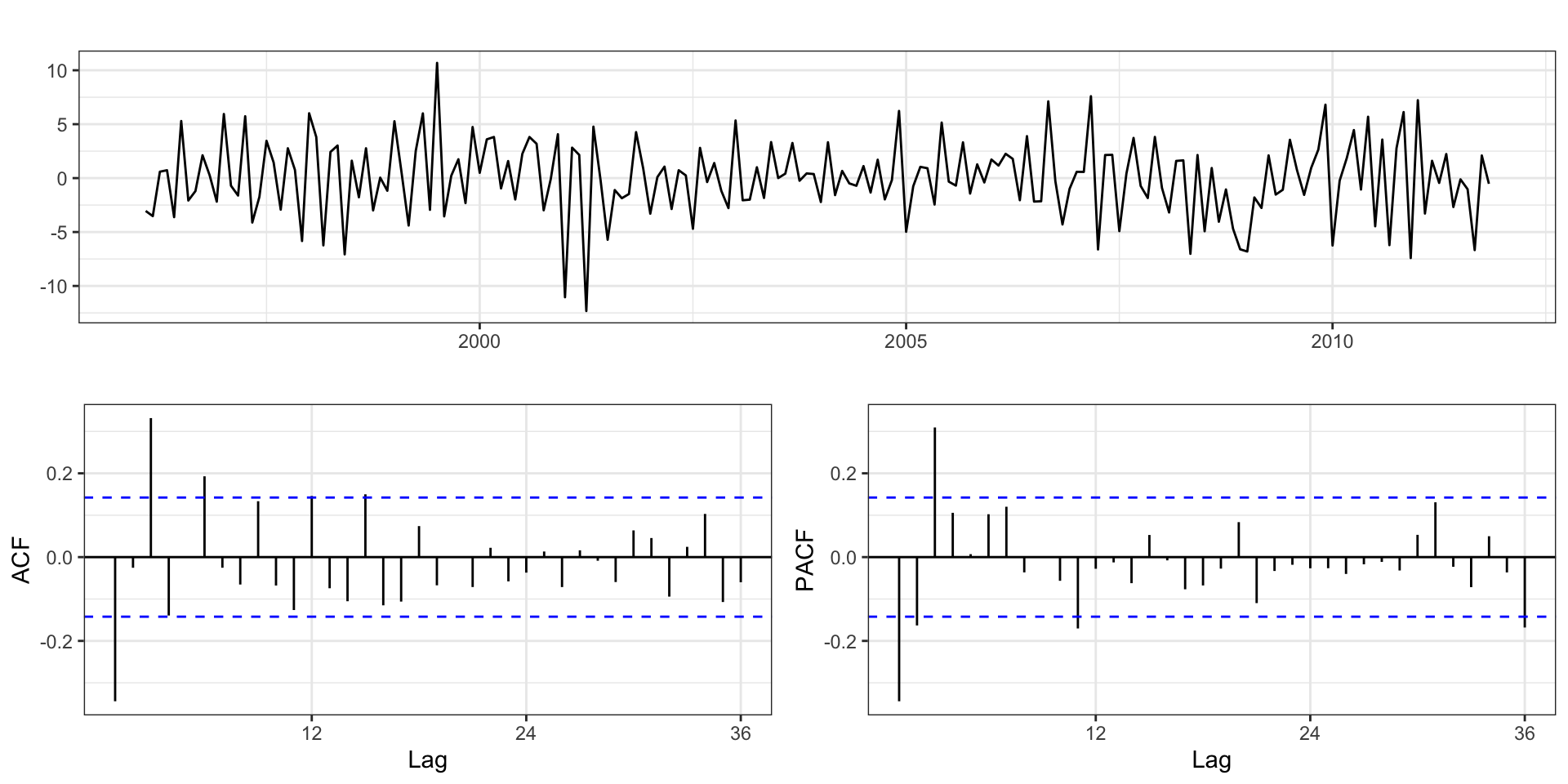
2nd order differencing
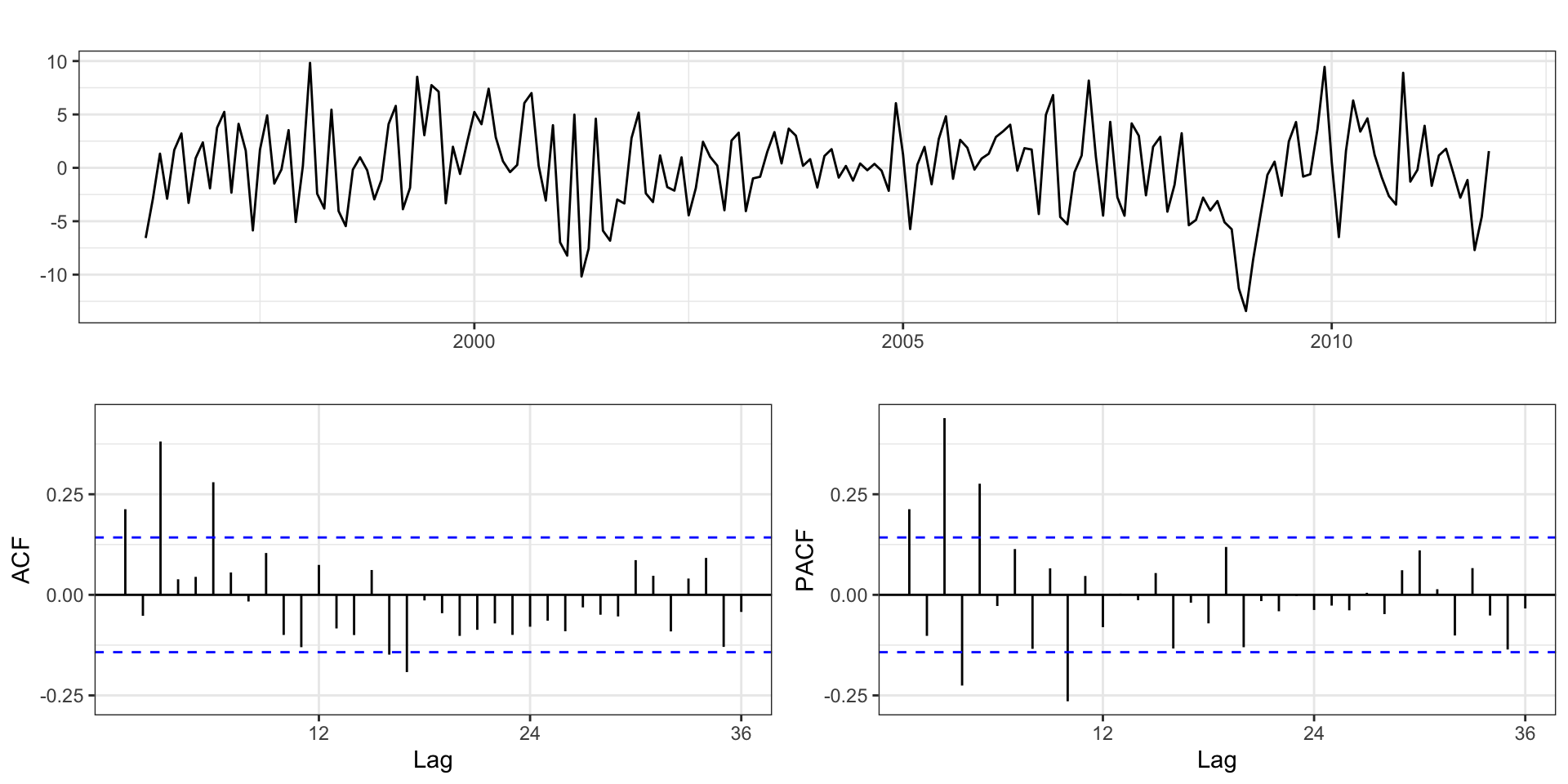
Model
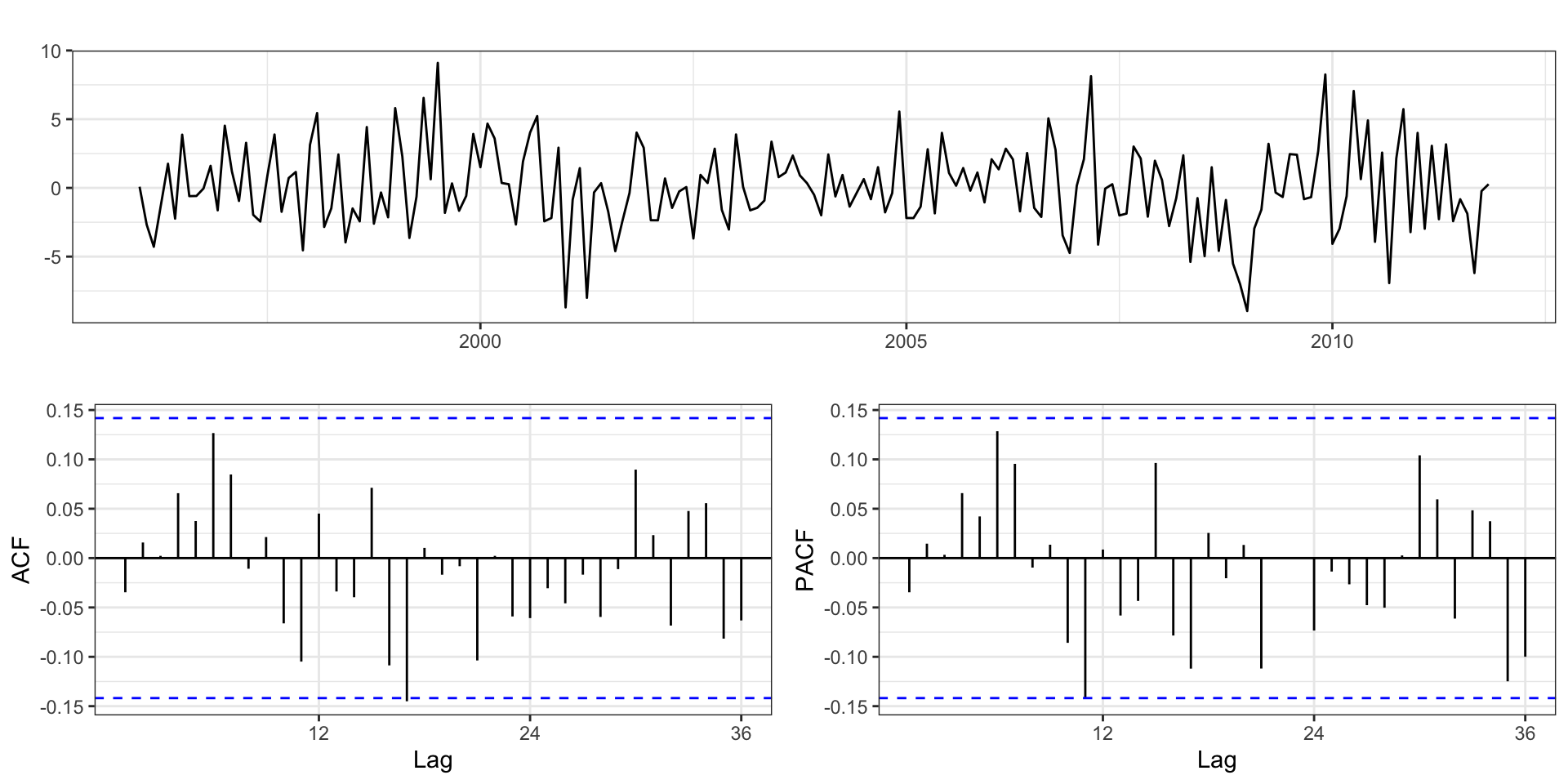
Residuals
Model Comparison
Model choices:
Automatic selection (AICc)
Automatic selection (BIC)
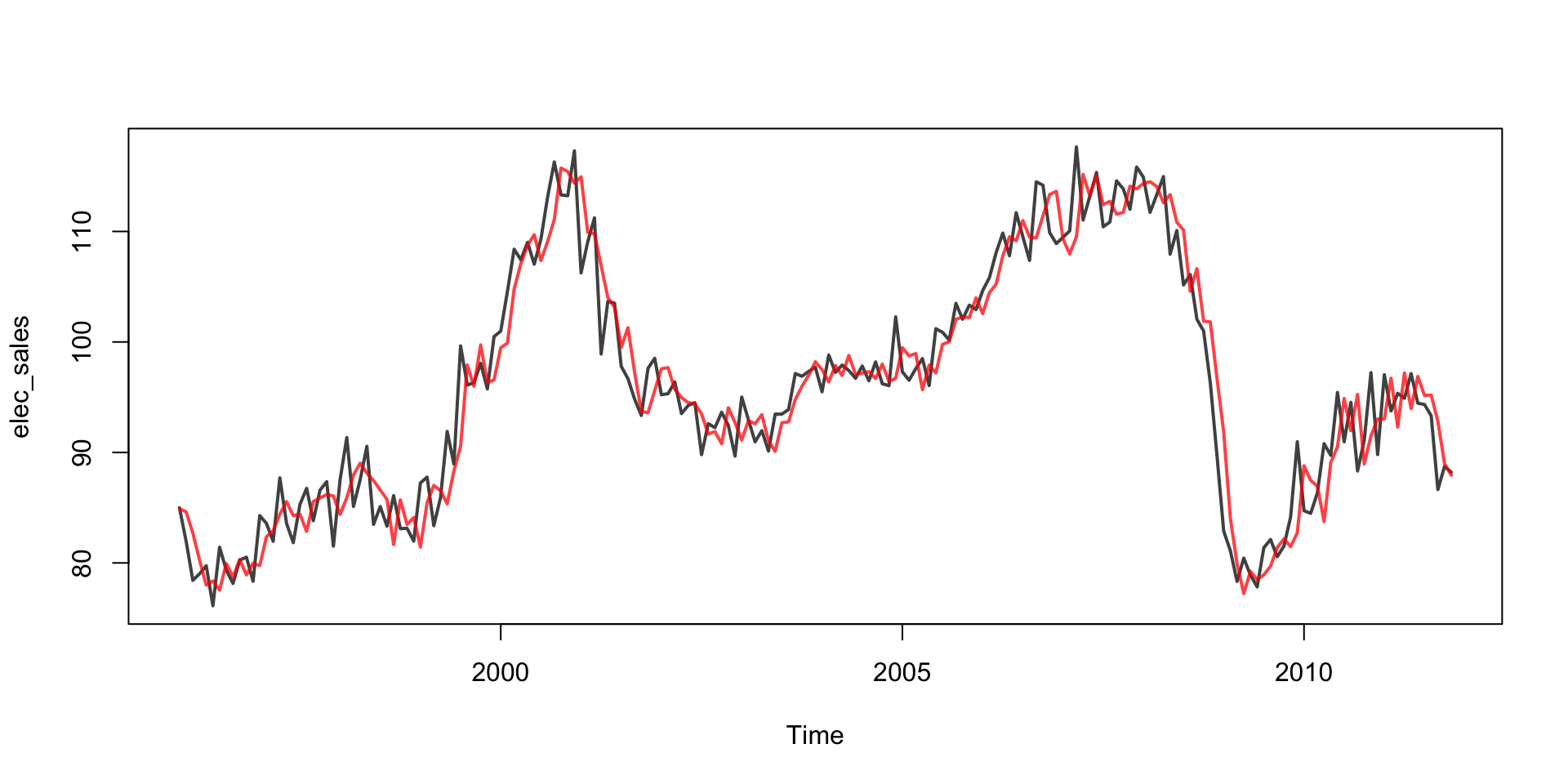
Model fit
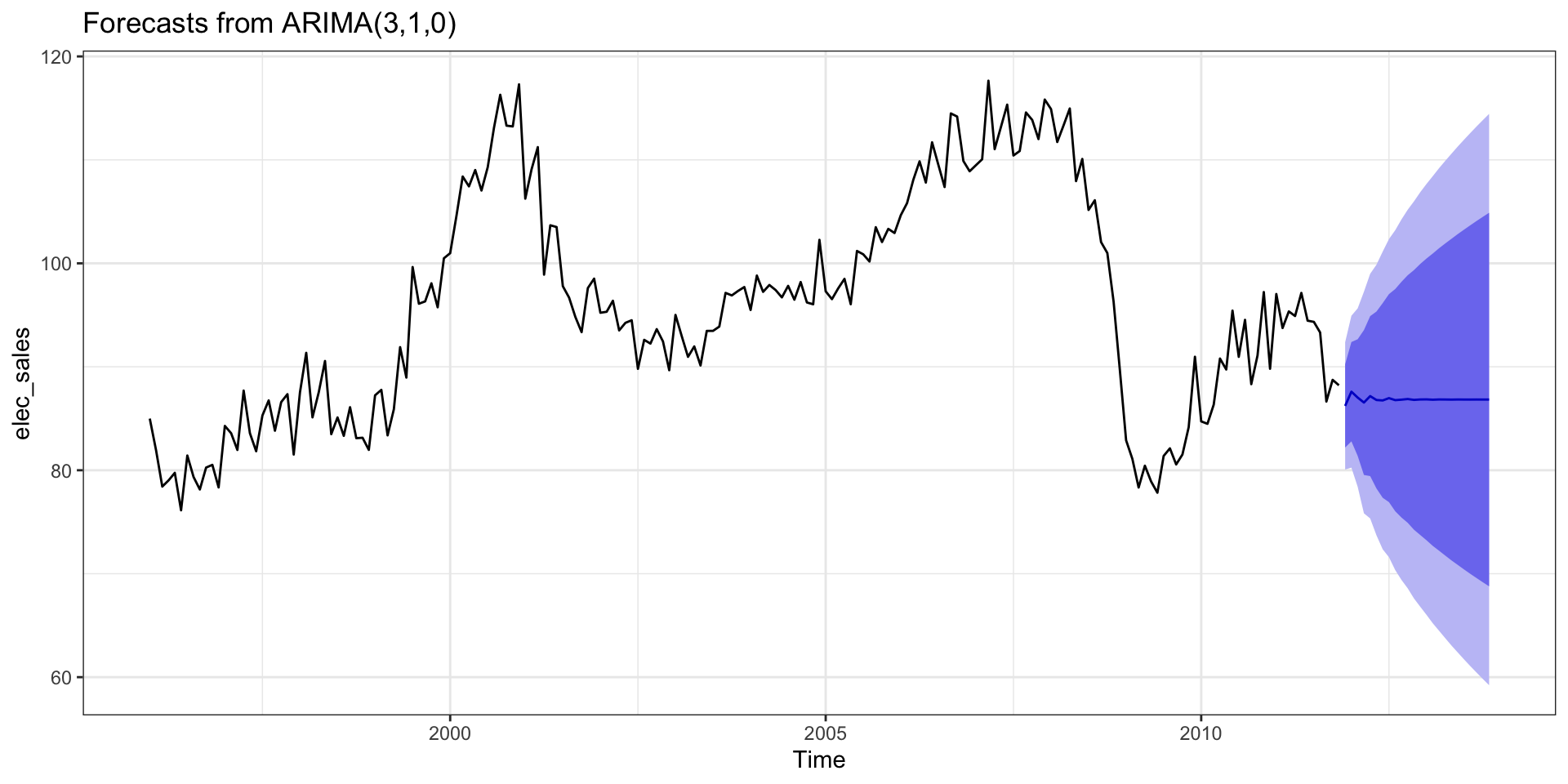
Model forecast
Model forecast - Zoom
Seasonal Models
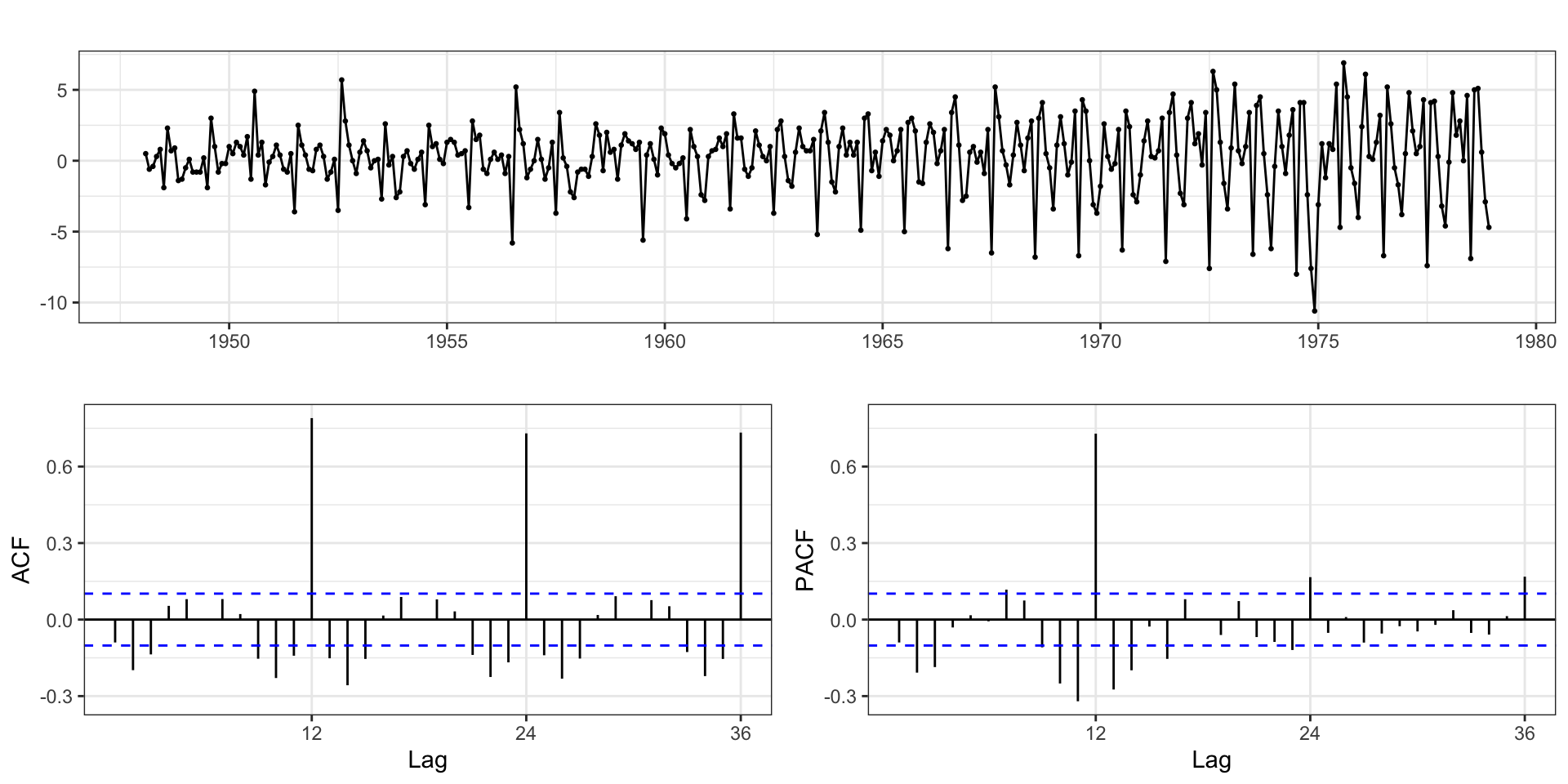
Australian Wine Sales Example
Australian total wine sales by wine makers in bottles <= 1 litre. Jan 1980 – Aug 1994.
Differencing
Seasonal Arima
We can extend the existing ARIMA model to handle these higher order lags (without having to include all of the intervening lags).
Seasonal \(\text{ARIMA}\,(p,d,q) \times (P,D,Q)_s\): \[ \Phi_P(L^s) \, \phi_p(L) \, \Delta_s^D \, \Delta^d \, y_t = \delta + \Theta_Q(L^s) \, \theta_q(L) \, w_t\] . . .
where
\[ \begin{aligned} \phi_p(L) &= 1-\phi_1 L - \phi_2 L^2 - \ldots - \phi_p L^p\\ \theta_q(L) &= 1+\theta_1 L + \theta_2 L^2 + \ldots + \theta_p L^q \\ \Delta^d &= (1-L)^d\\ \\ \Phi_P(L^s) &= 1-\Phi_1 L^s - \Phi_2 L^{2s} - \ldots - \Phi_P L^{Ps} \\ \Theta_Q(L^s) &= 1+\Theta_1 L + \Theta_2 L^{2s} + \ldots + \theta_p L^{Qs} \\ \Delta_s^D &= (1-L^s)^D\\ \end{aligned} \]
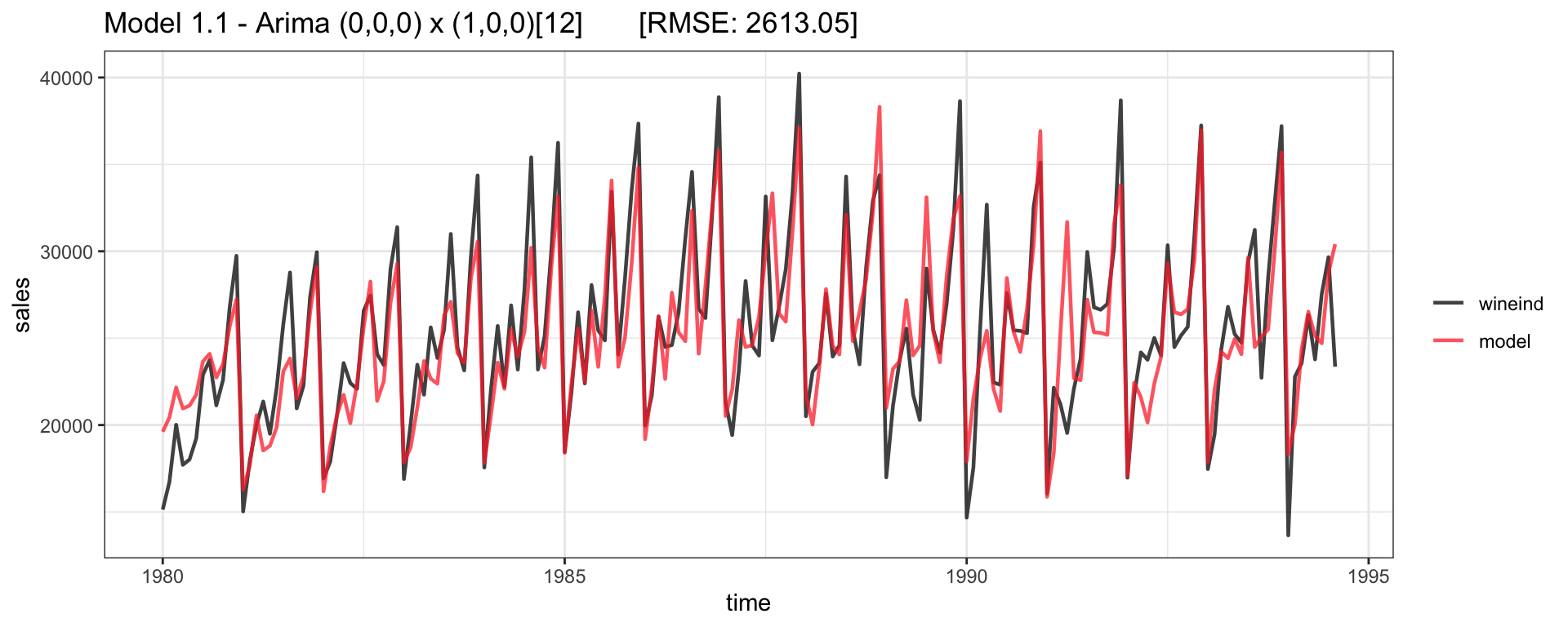
Seasonal ARIMA - AR
Lets consider an \(\text{ARIMA}(0,0,0) \times (1,0,0)_{12}\): \[ \begin{aligned} (1-\Phi_1 L^{12}) \, y_t = \delta + w_t \\ y_t = \Phi_1 y_{t-12} + \delta + w_t \end{aligned} \]
Fitted - Model 1.1
Seasonal Arima - Diff
Lets consider an \(\text{ARIMA}(0,0,0) \times (0,1,0)_{12}\): \[ \begin{aligned} (1 - L^{12}) \, y_t = \delta + w_t \\ y_t = y_{t-12} + \delta + w_t \end{aligned} \]
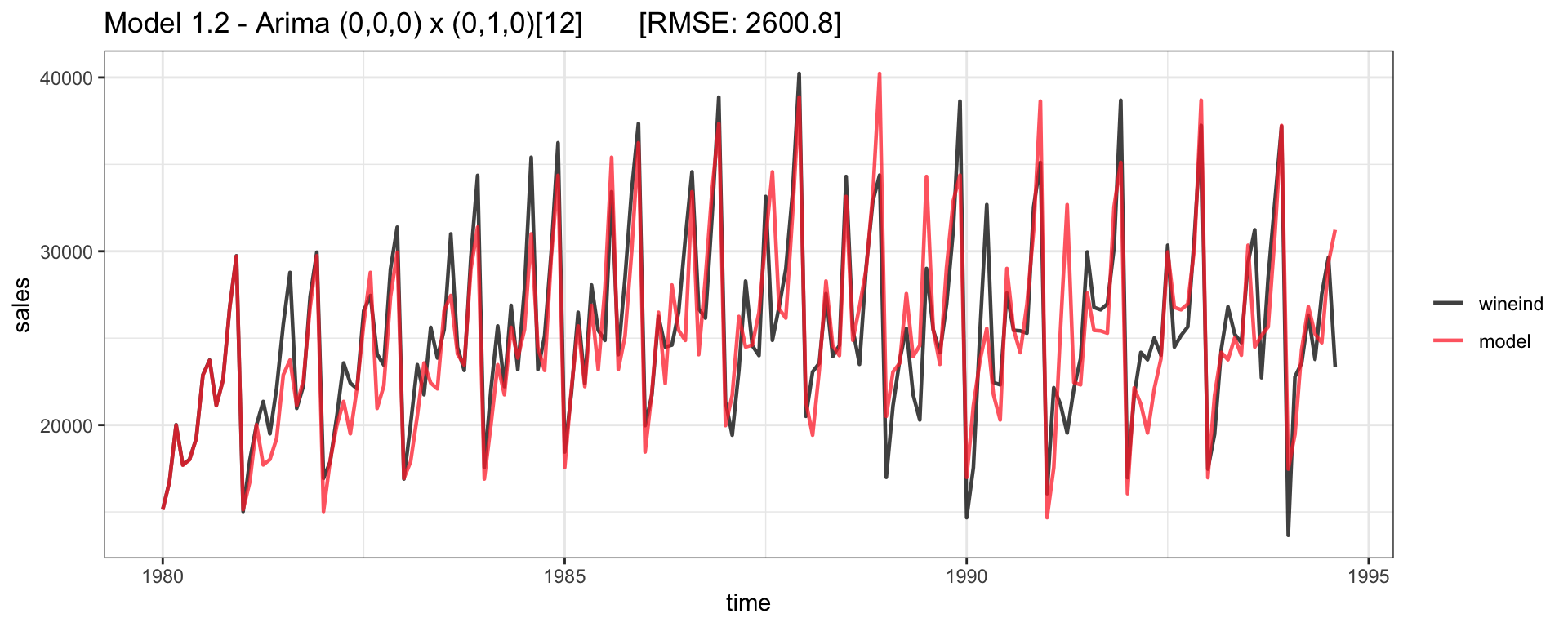
Fitted - Model 1.2
Residuals - Model 1.1 (SAR)
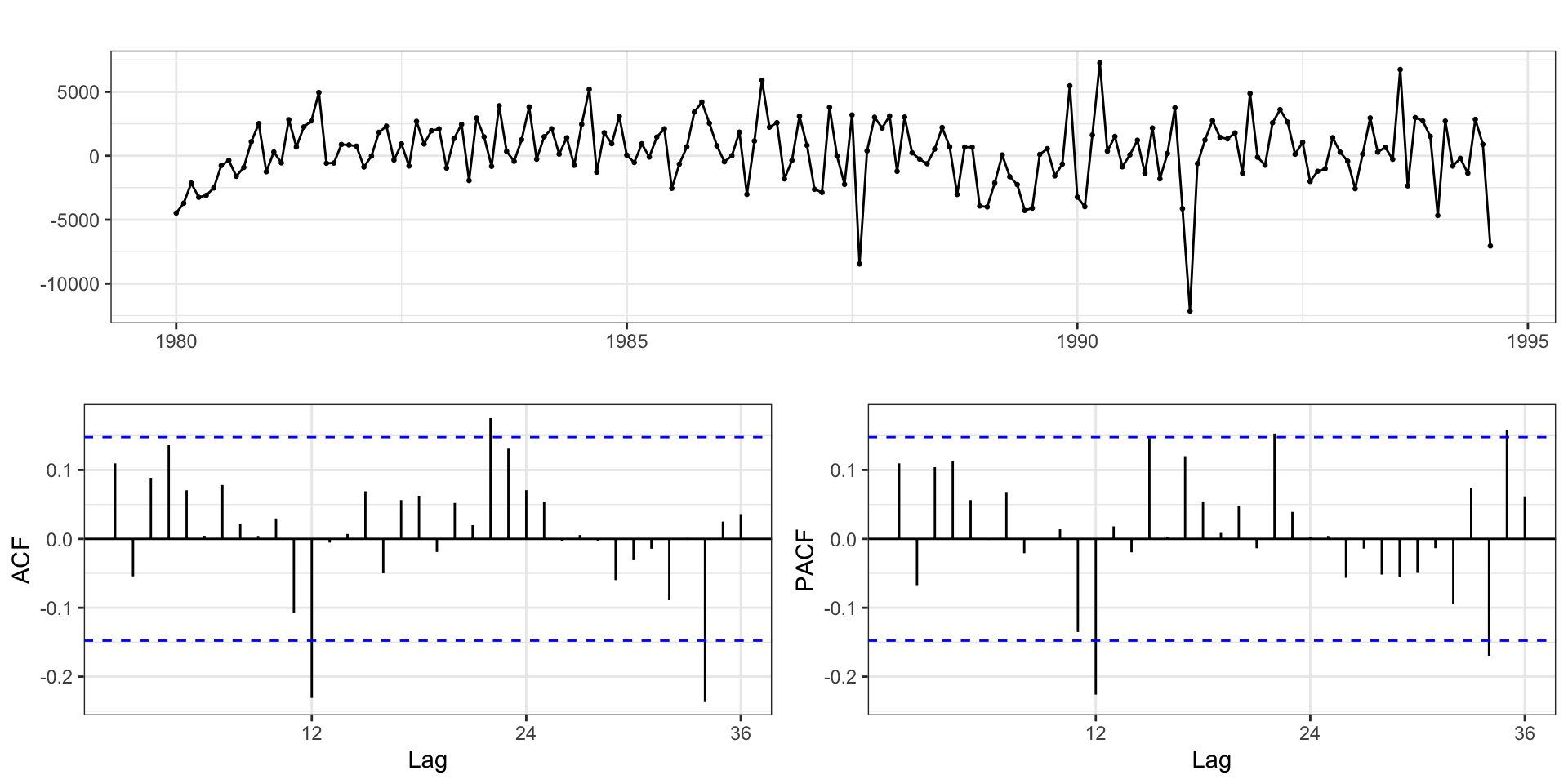
Residuals - Model 1.2 (SDiff)
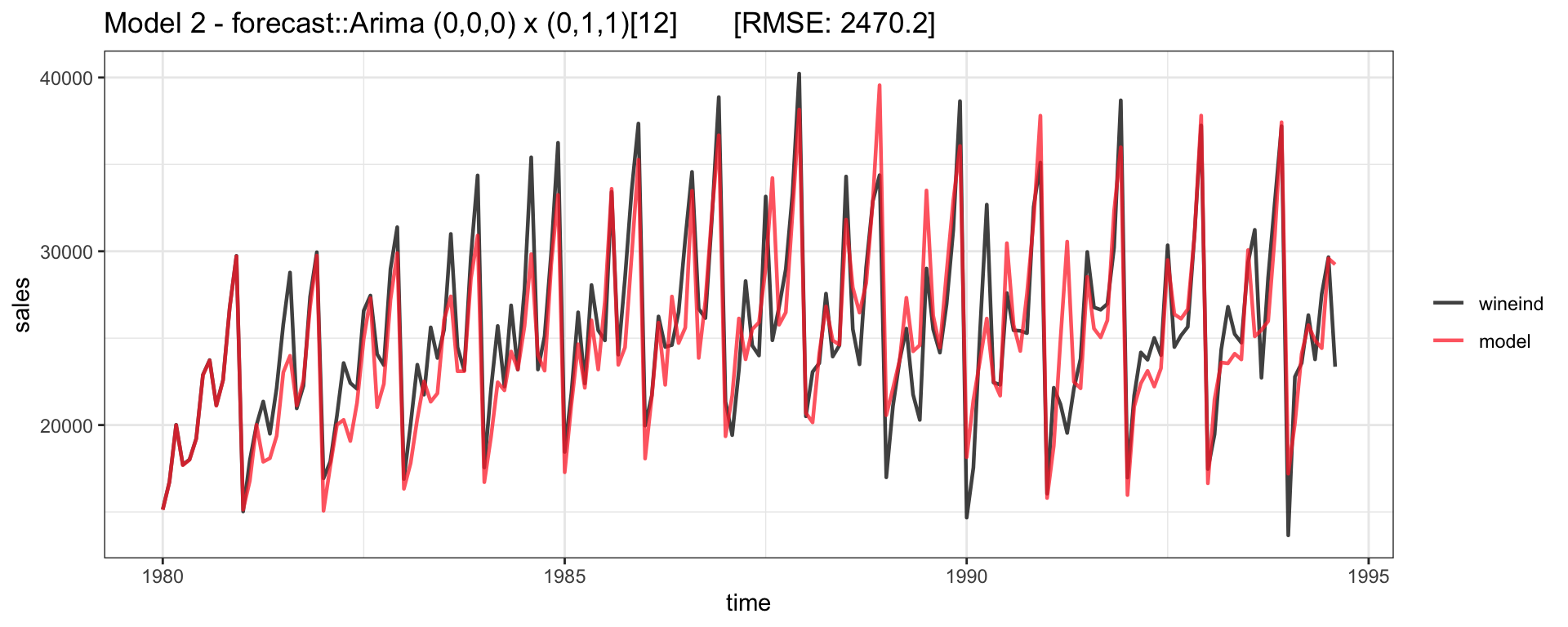
Model 2
\(\text{ARIMA}(0,0,0) \times (0,1,1)_{12}\):
\[ \begin{aligned} (1-L^{12}) y_t = \delta + (1+\Theta_1 L^{12}) w_t \\ y_t = \delta + y_{t-12} + w_t + \Theta_1 w_{t-12} \end{aligned} \]
Fitted - Model 2
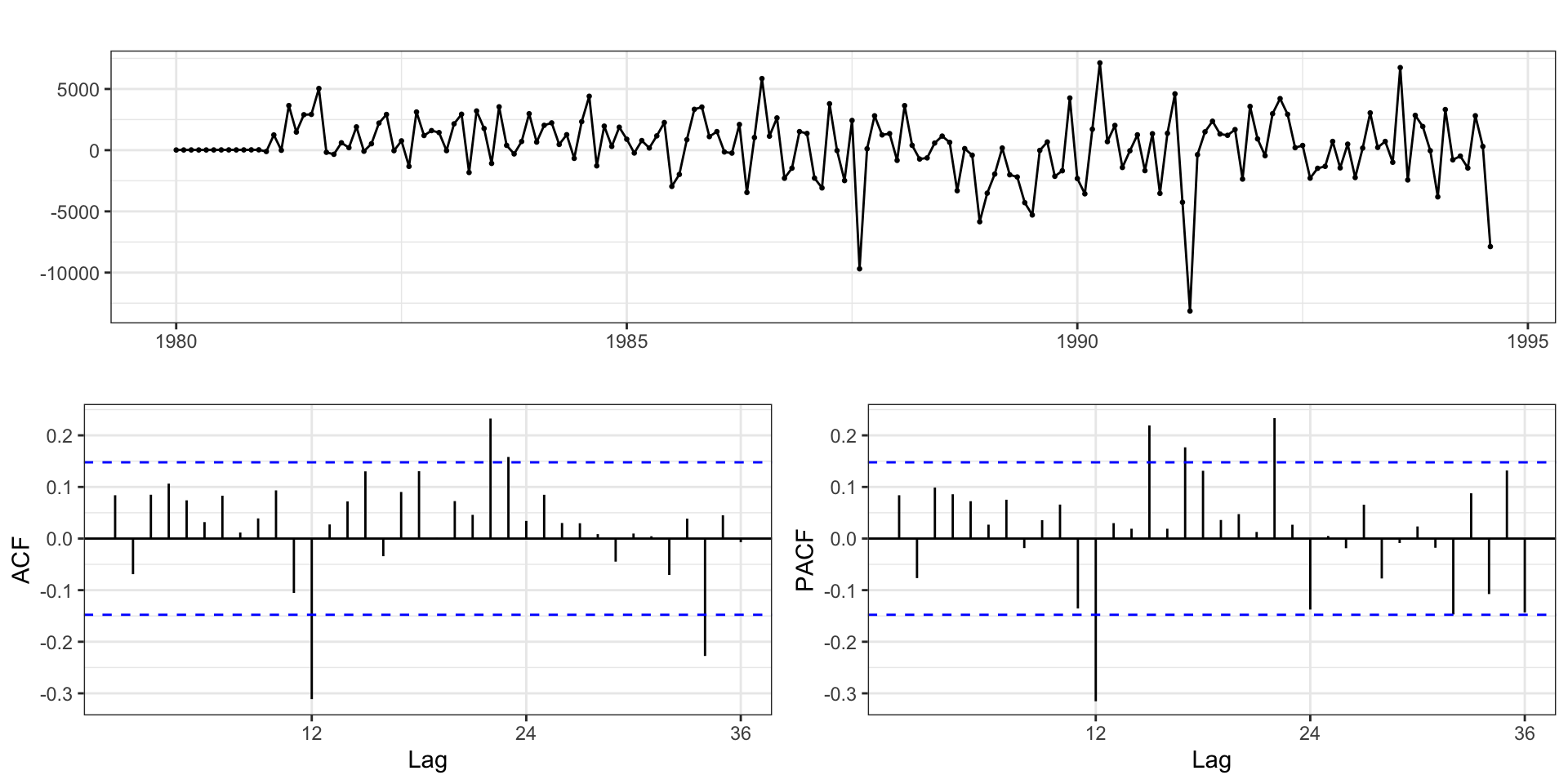
Residuals
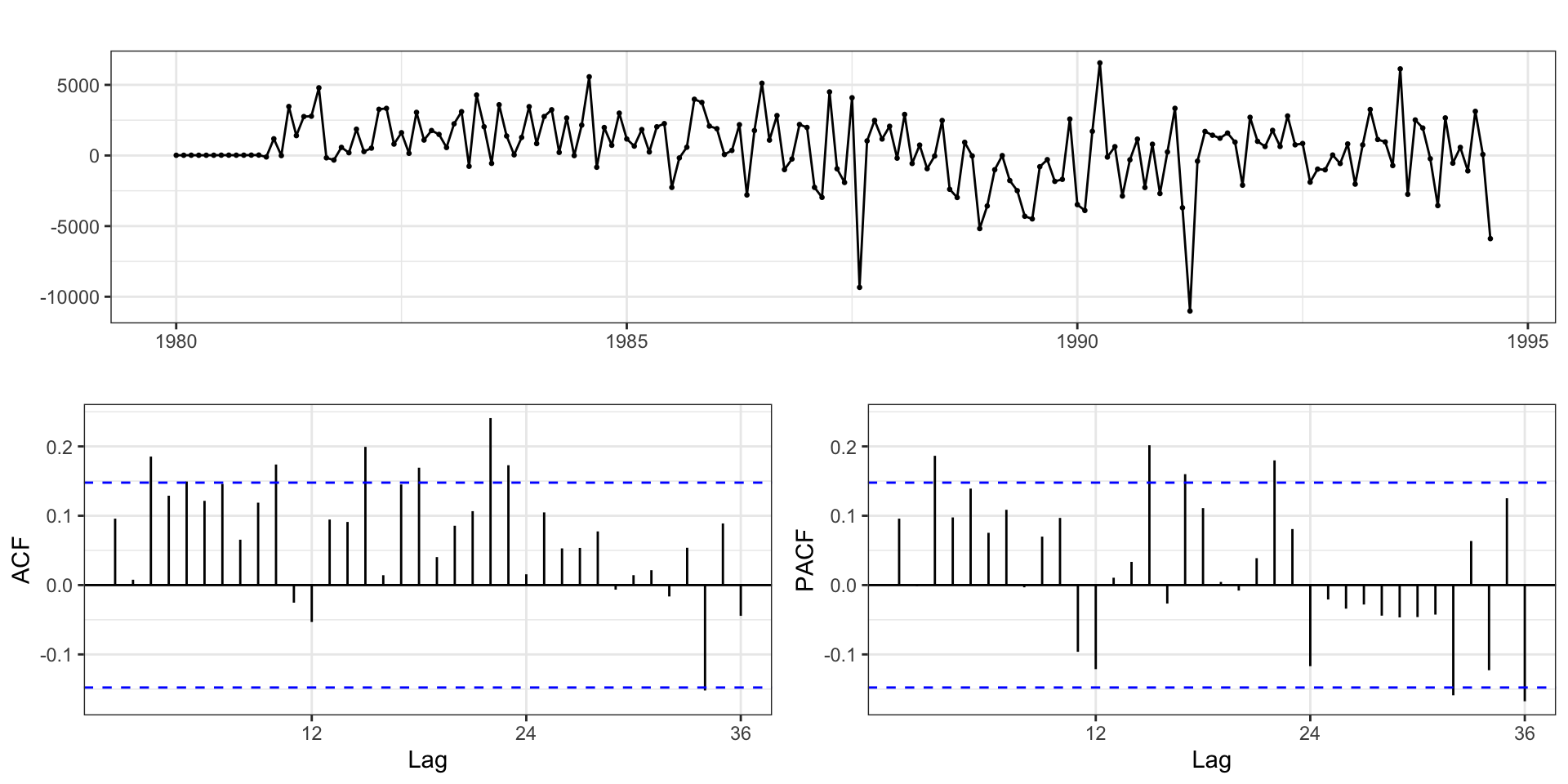
Model 3
\(\text{ARIMA}(3,0,0) \times (0,1,1)_{12}\)
\[ \begin{aligned} (1-\phi_1 L - \phi_2 L^2 - \phi_3 L^3) \, (1-L^{12}) y_t = \delta + (1 + \Theta_1 L)w_t \\ y_t = \delta + \sum_{i=1}^3 \phi_i y_{t-i} + y_{t-12} - \sum_{i=1}^3 \phi_i y_{t-12-i} + w_t + w_{t-12} \end{aligned} \]
Series: wineind
ARIMA(3,0,0)(0,1,1)[12]
Coefficients:
ar1 ar2 ar3 sma1
0.1402 0.0806 0.3040 -0.5790
s.e. 0.0755 0.0813 0.0823 0.1023
sigma^2 = 5948935: log likelihood = -1512.38
AIC=3034.77 AICc=3035.15 BIC=3050.27Fitted model
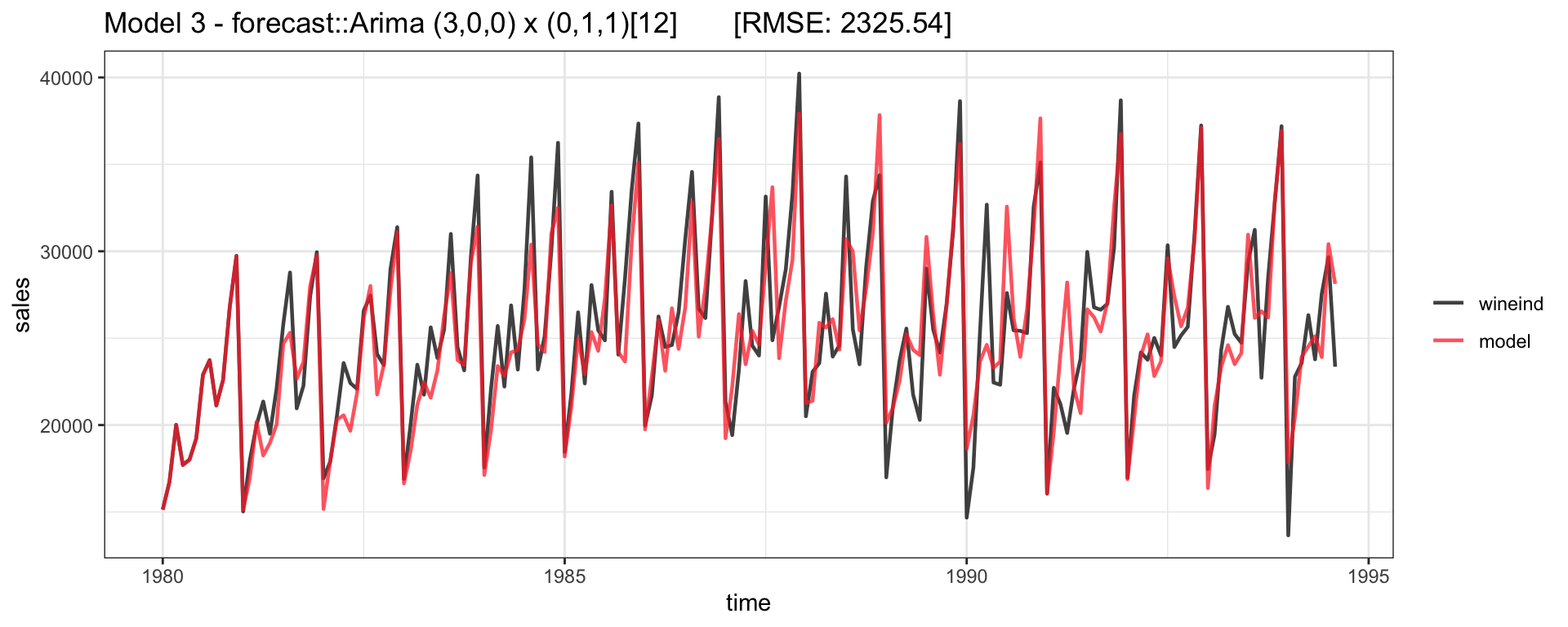
Model - Residuals
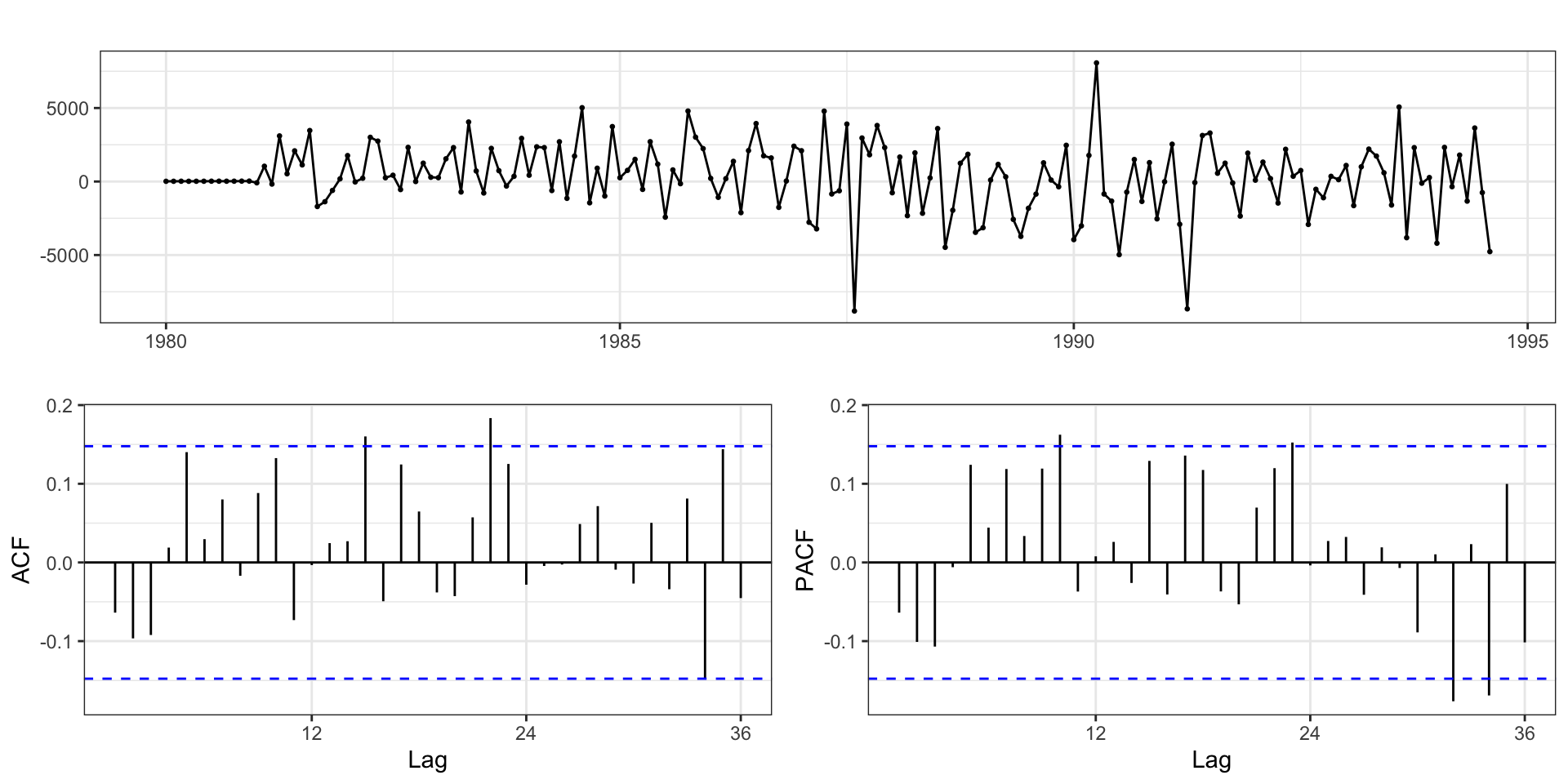
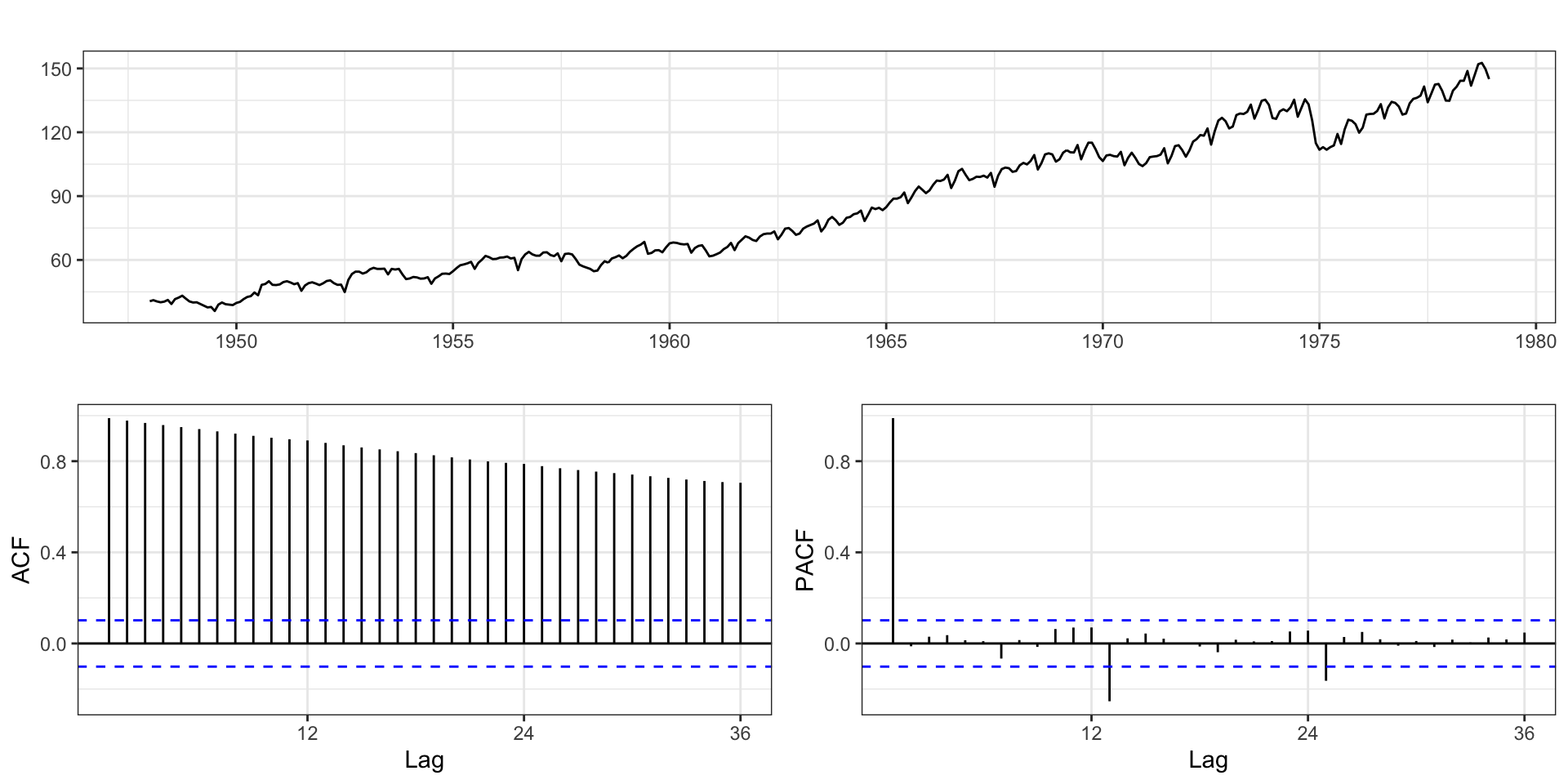
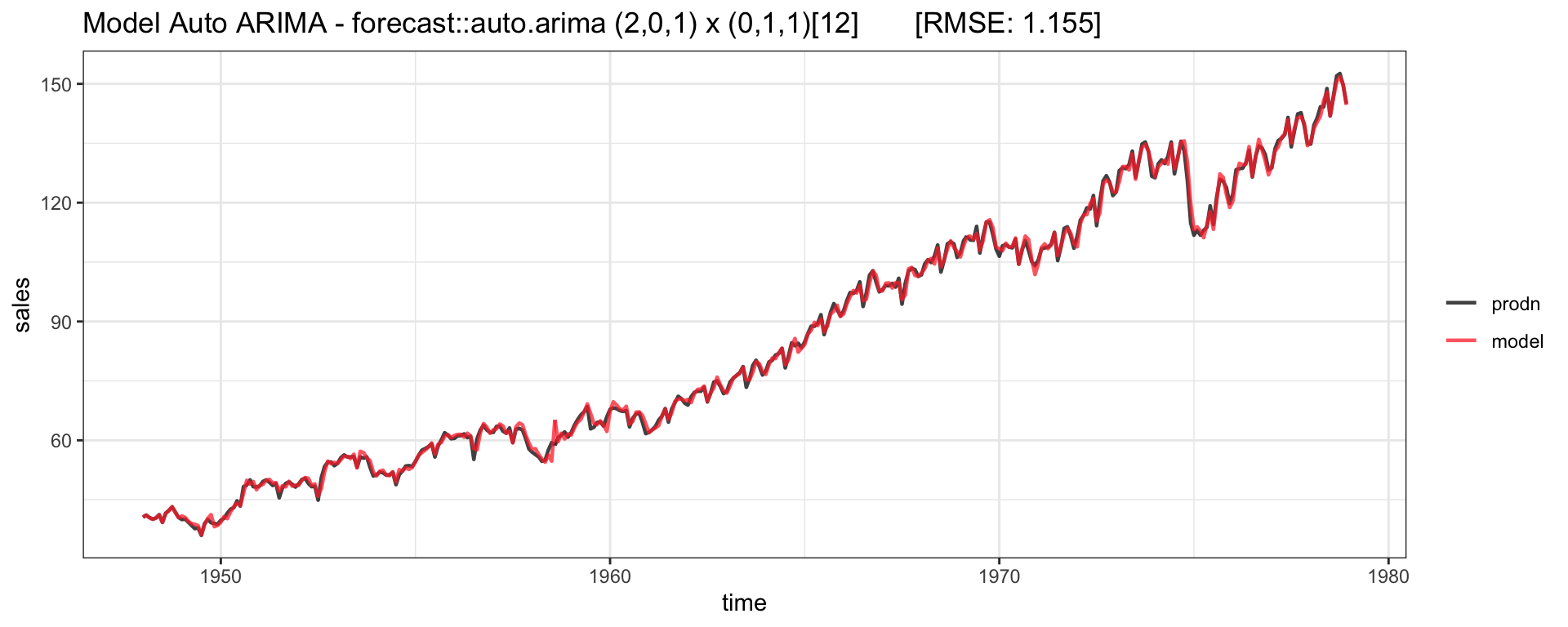
Federal Reserve Board Production Index
prodn from the astsa package
Monthly Federal Reserve Board Production Index (1948-1978)
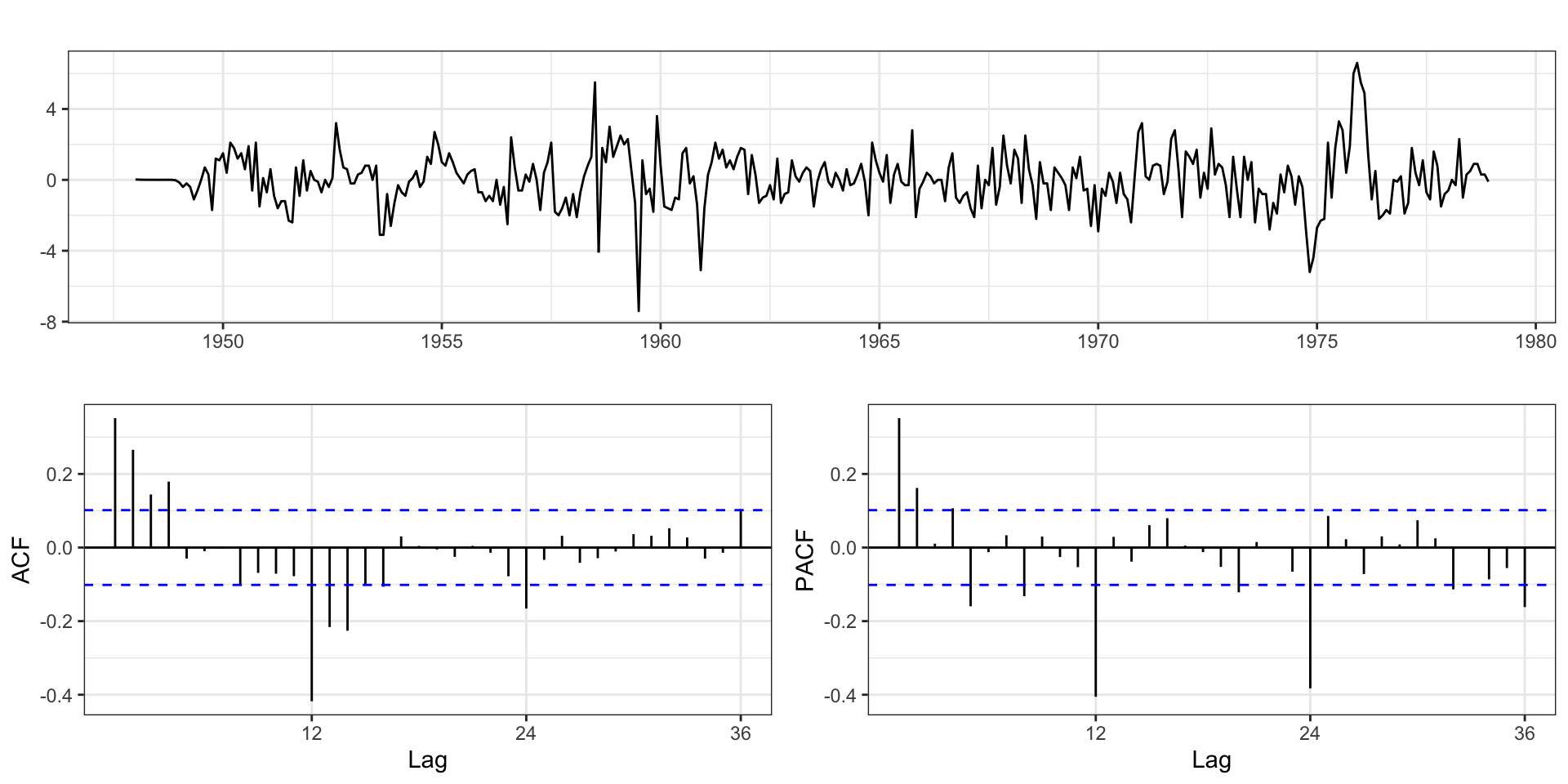
Differencing
Based on the ACF it seems like standard differencing may be required
Differencing + Seasonal Differencing
Additional seasonal differencing also seems warranted
Residuals - Model 2
Adding Seasonal MA
Adding Seasonal MA (cont.)
Residuals - Model 3.3
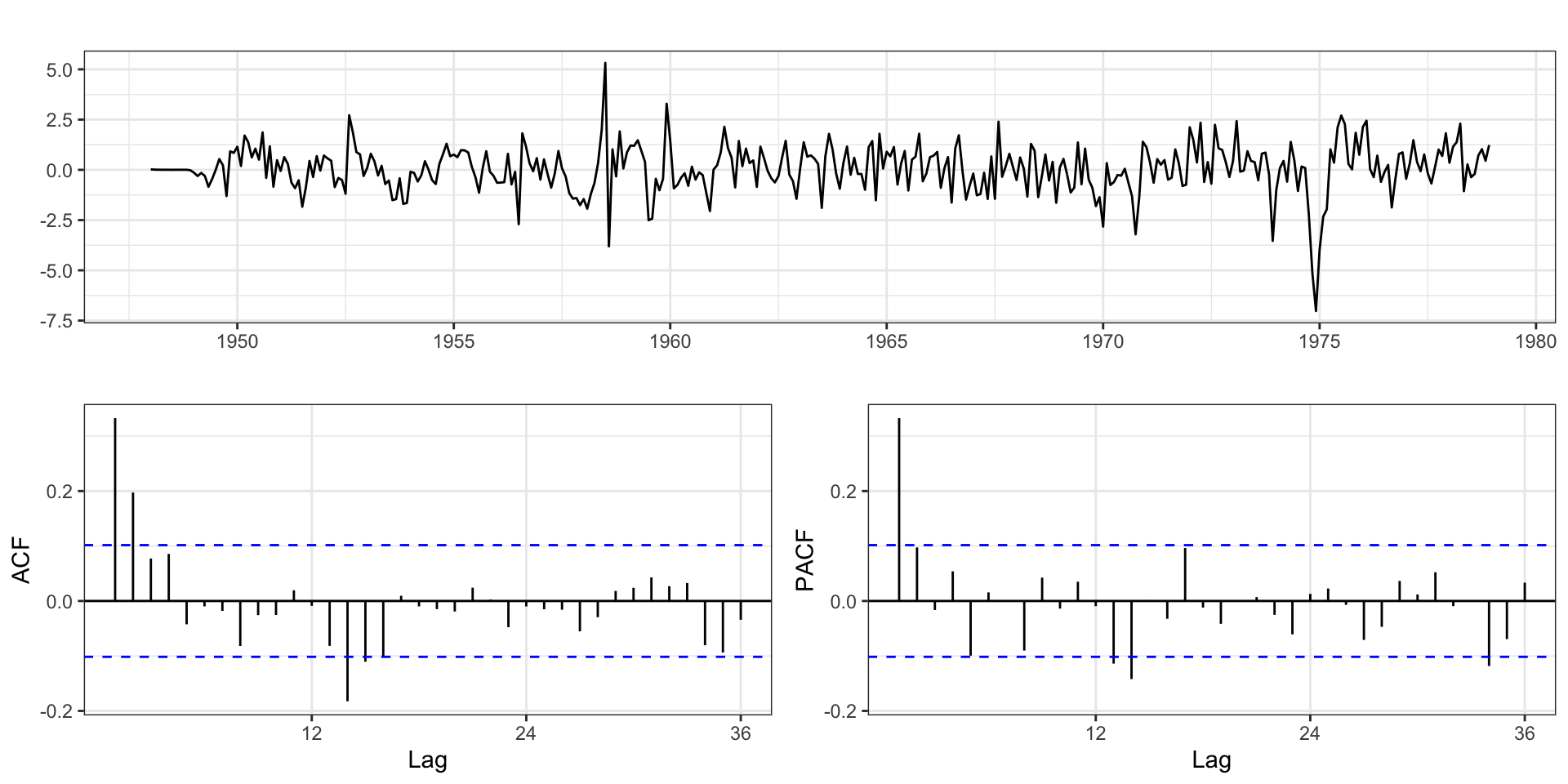
Adding AR
Series: prodn
ARIMA(1,1,0)(0,1,3)[12]
Coefficients:
ar1 sma1 sma2 sma3
0.3393 -0.7619 -0.1222 0.2756
s.e. 0.0500 0.0527 0.0646 0.0525
sigma^2 = 1.341: log likelihood = -565.98
AIC=1141.95 AICc=1142.12 BIC=1161.37Series: prodn
ARIMA(2,1,0)(0,1,3)[12]
Coefficients:
ar1 ar2 sma1 sma2 sma3
0.3038 0.1077 -0.7393 -0.1445 0.2815
s.e. 0.0526 0.0538 0.0539 0.0653 0.0526
sigma^2 = 1.331: log likelihood = -563.98
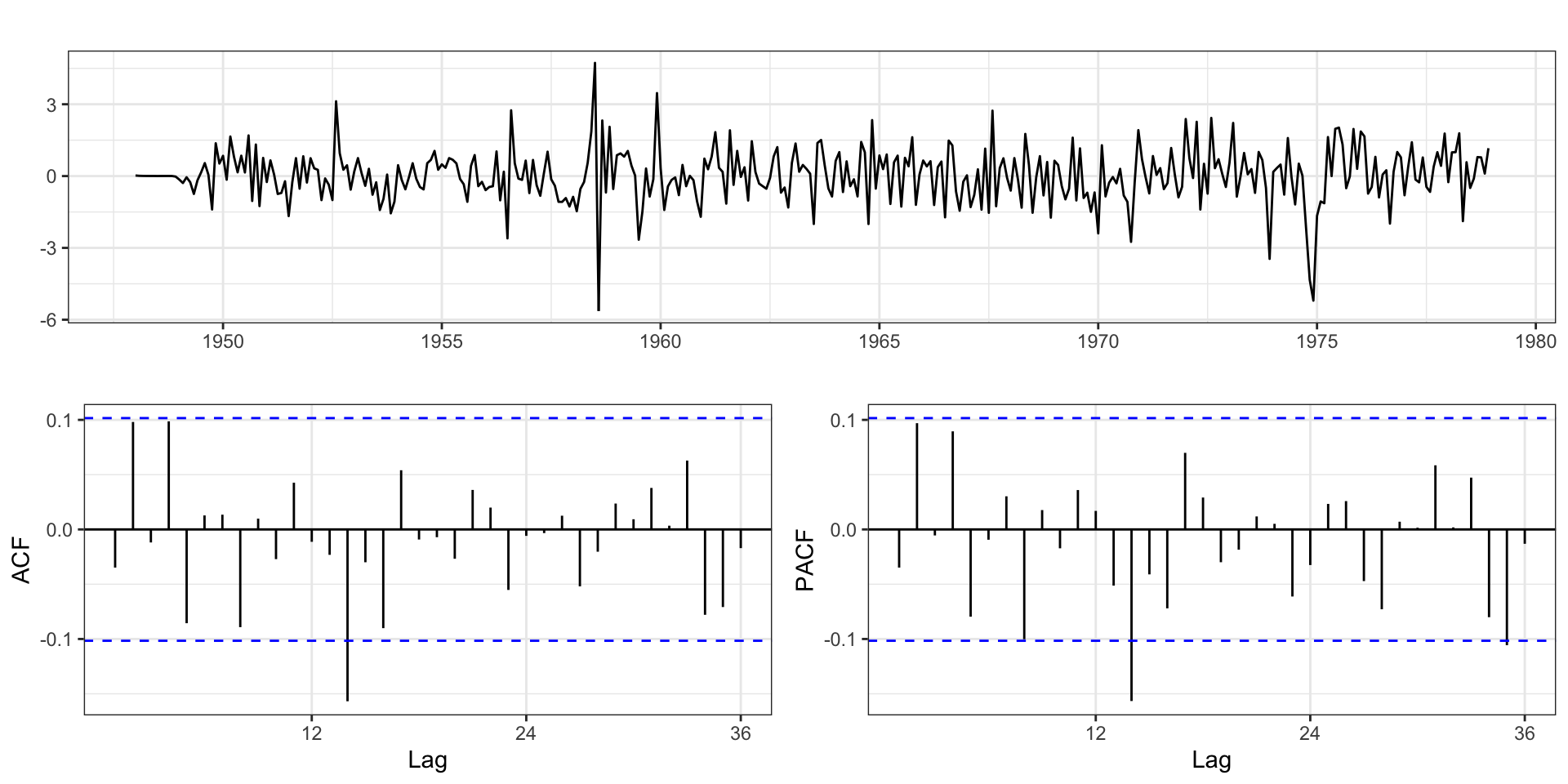
AIC=1139.97 AICc=1140.2 BIC=1163.26Residuals - Model 4.1
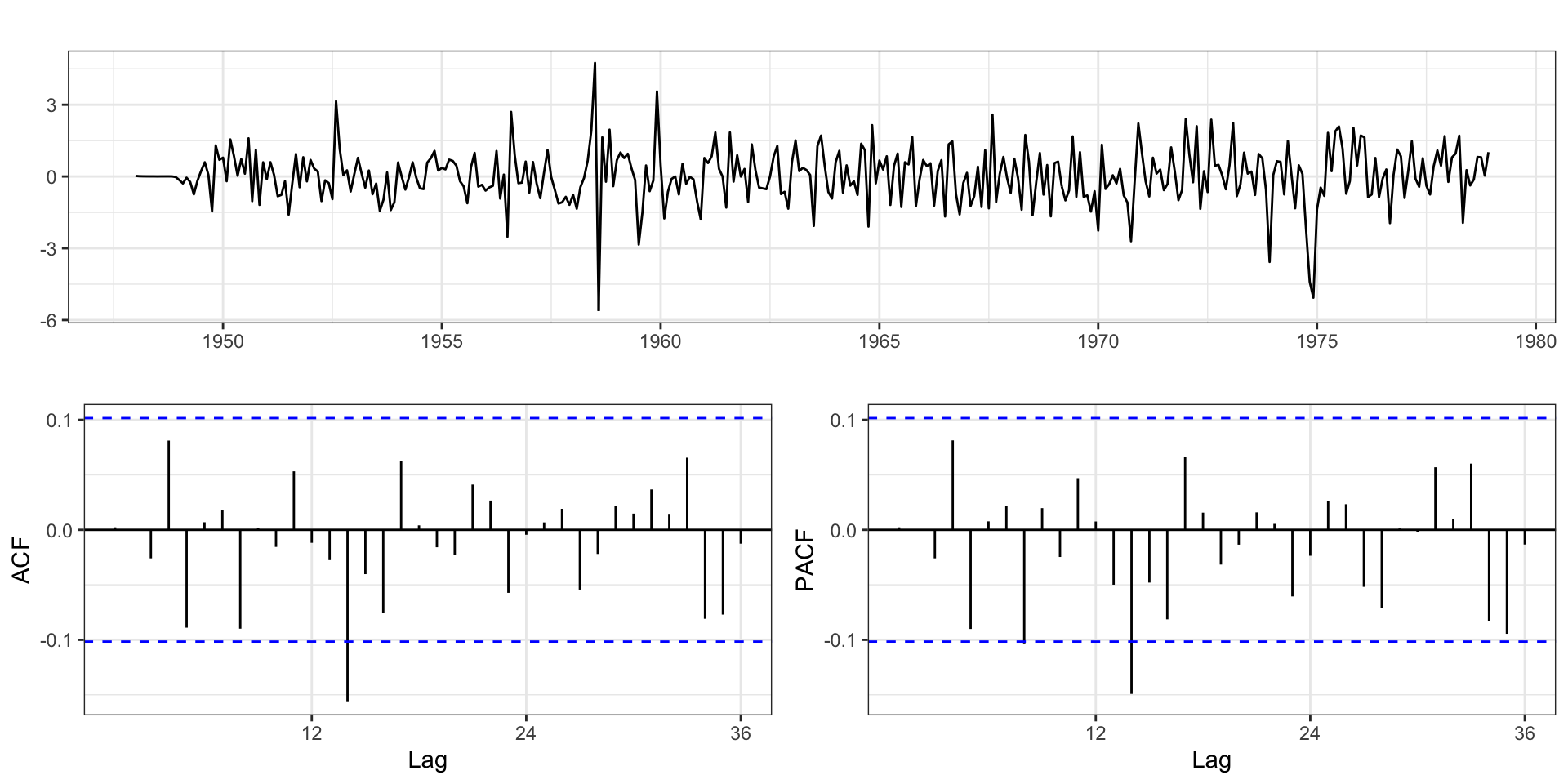
Residuals - Model 4.2
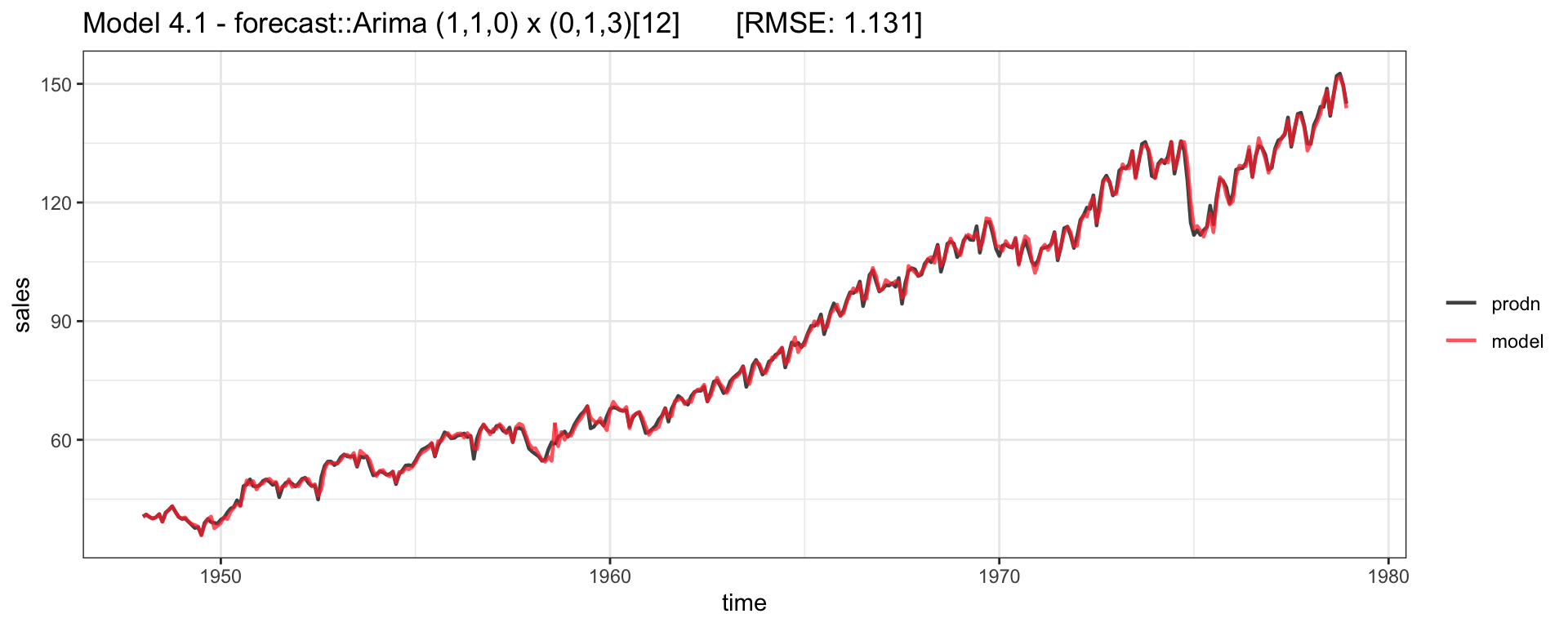
Model Fit
Model Forecast
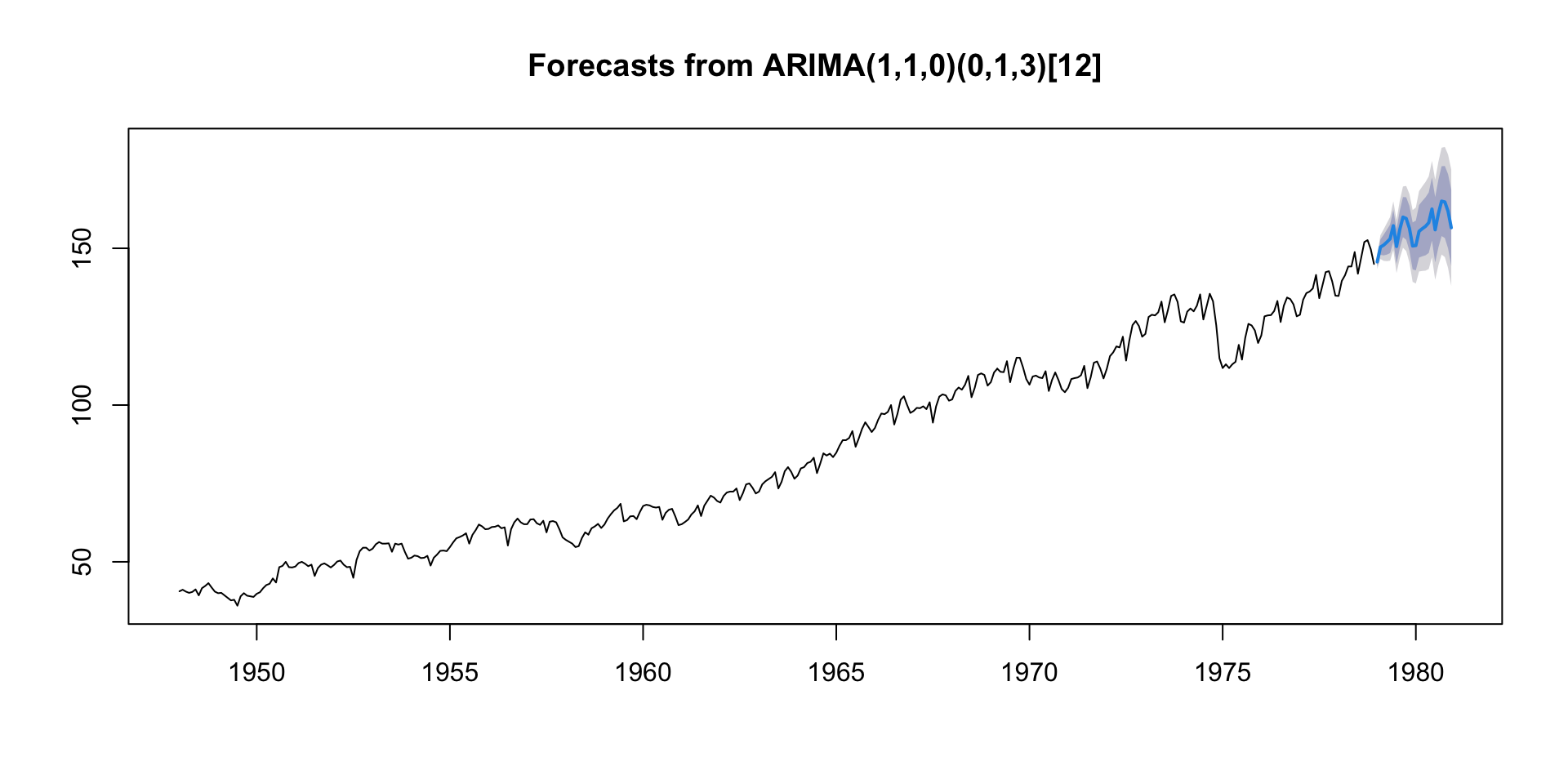
Model Forecast (cont.)
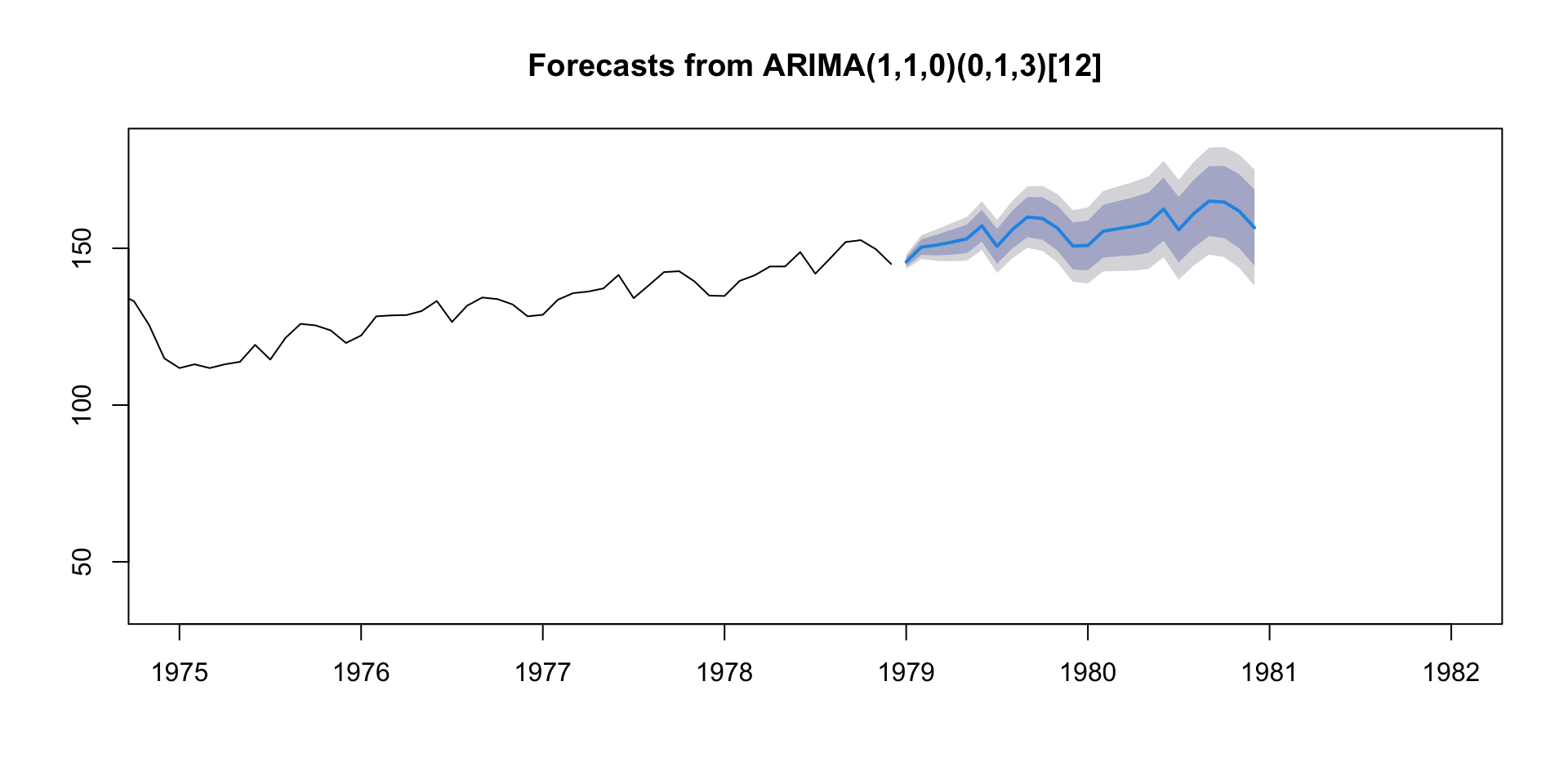
Model Forecast (cont.)
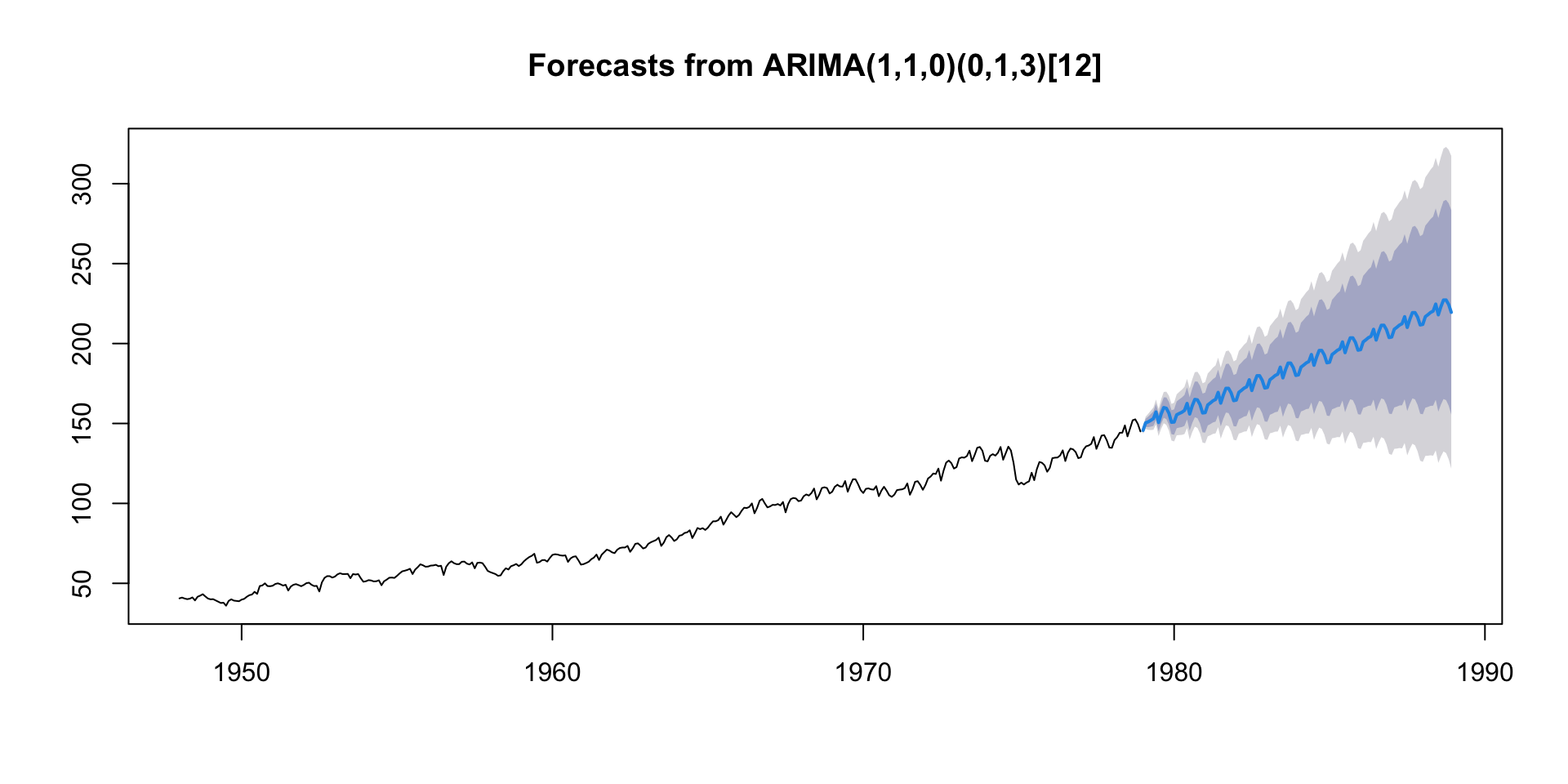
Model Forecast (cont.)
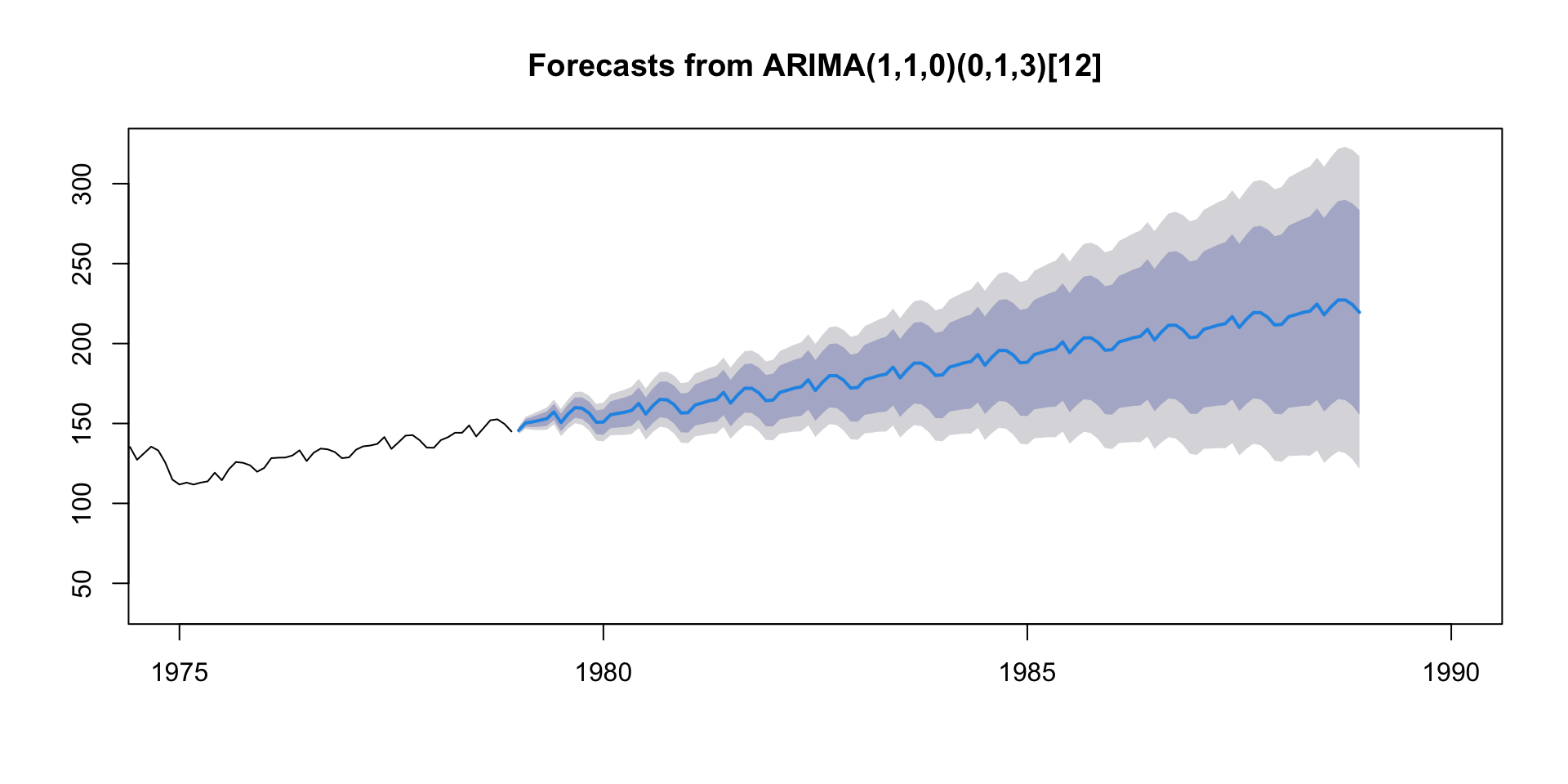
Auto ARIMA - Model Fit
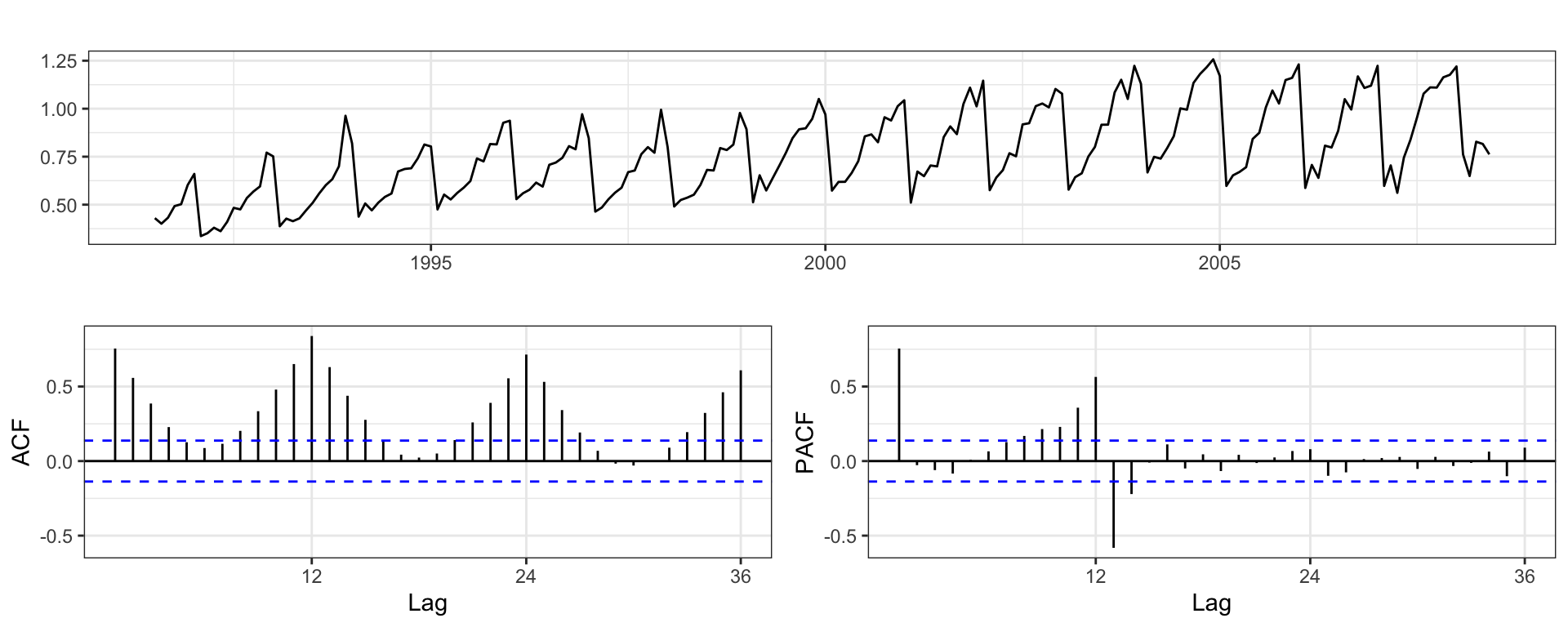
Exercise - Cortecosteroid Drug Sales
Monthly cortecosteroid drug sales in Australia from 1992 to 2008.
Sta 344 - Fall 2022