Logistic Regression and Residual Analysis
Lecture 05
Dr. Colin Rundel
Lecture 4 wrap up
Last time
Model Fit
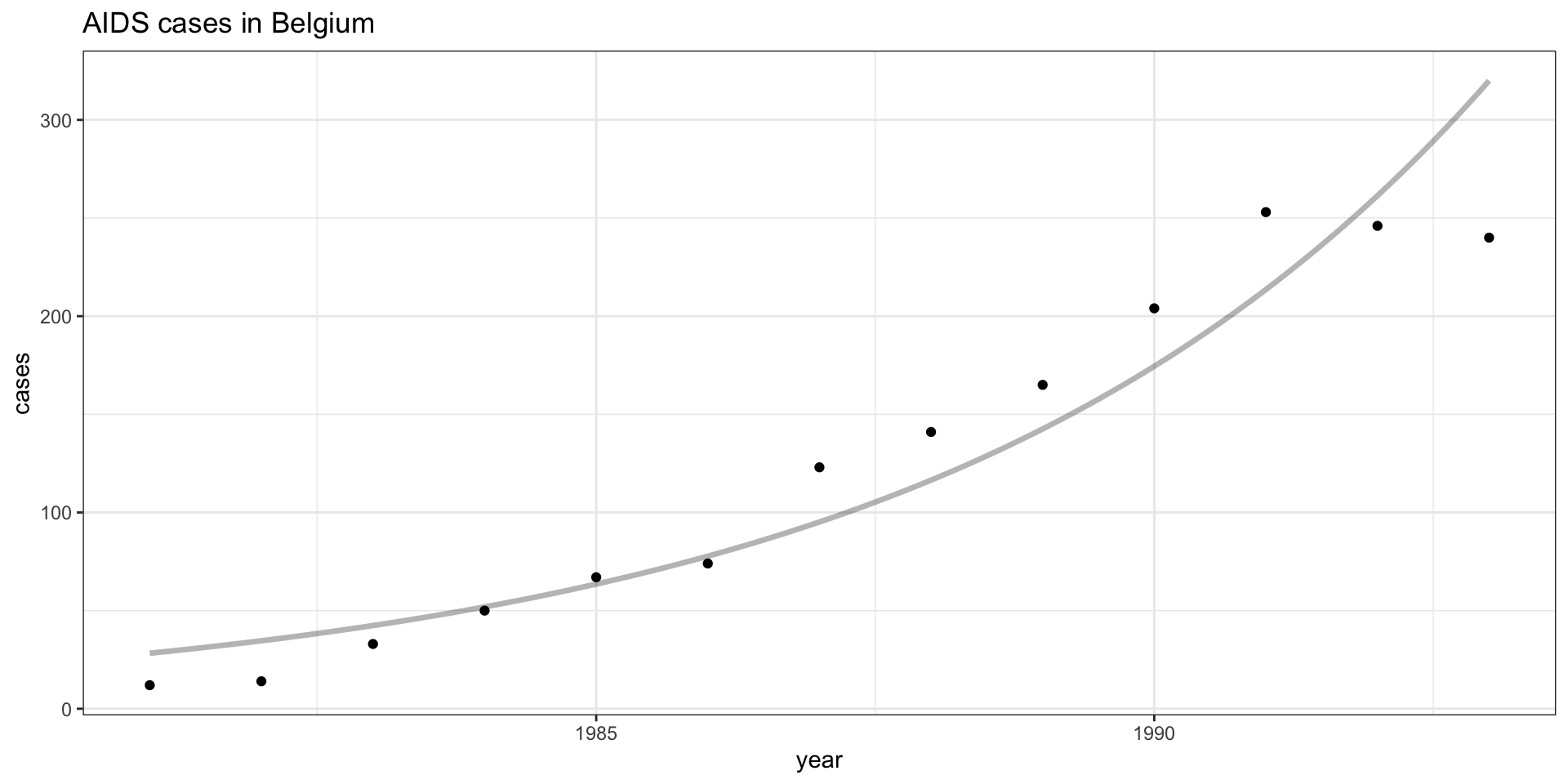
Residuals
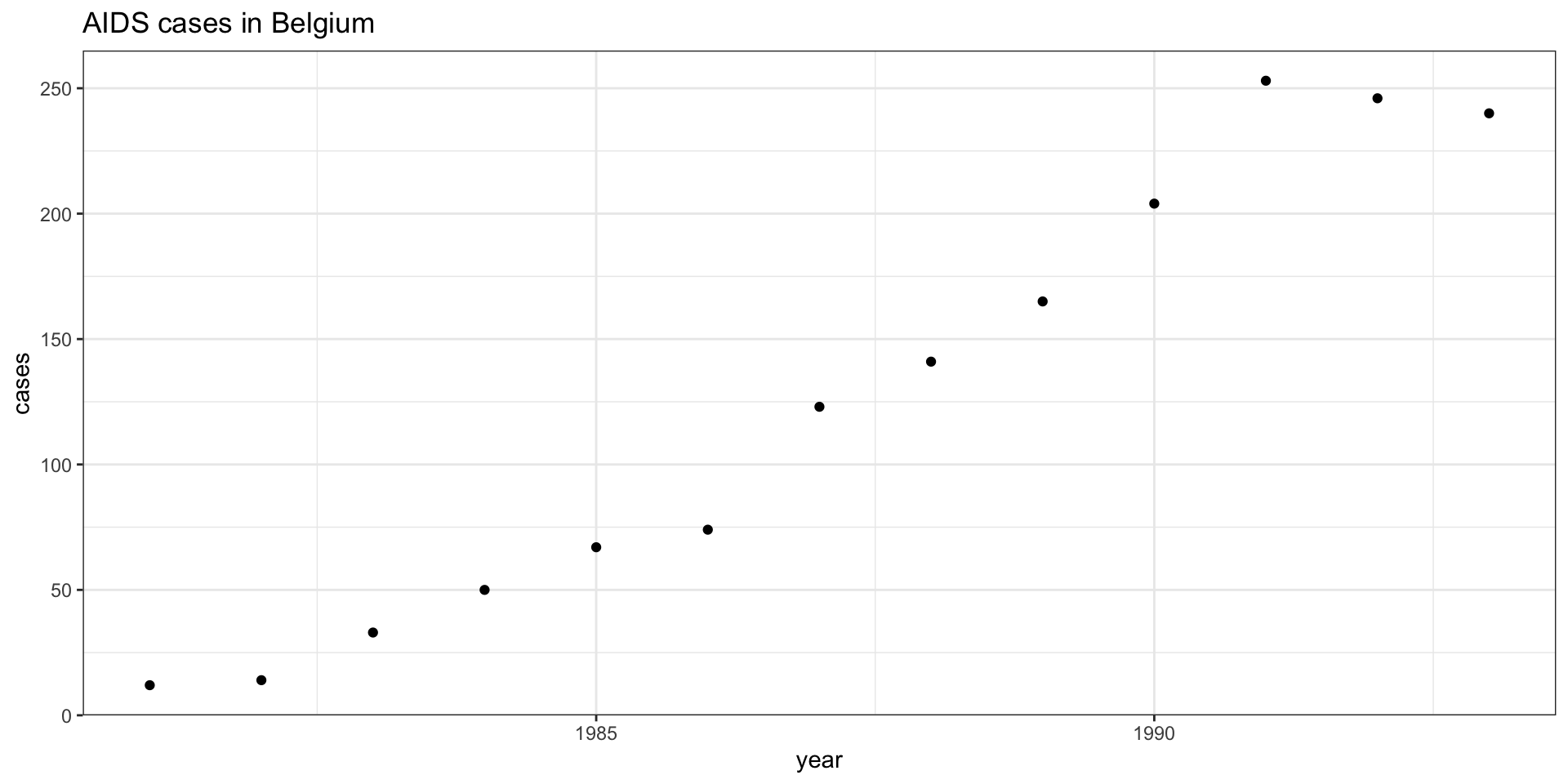
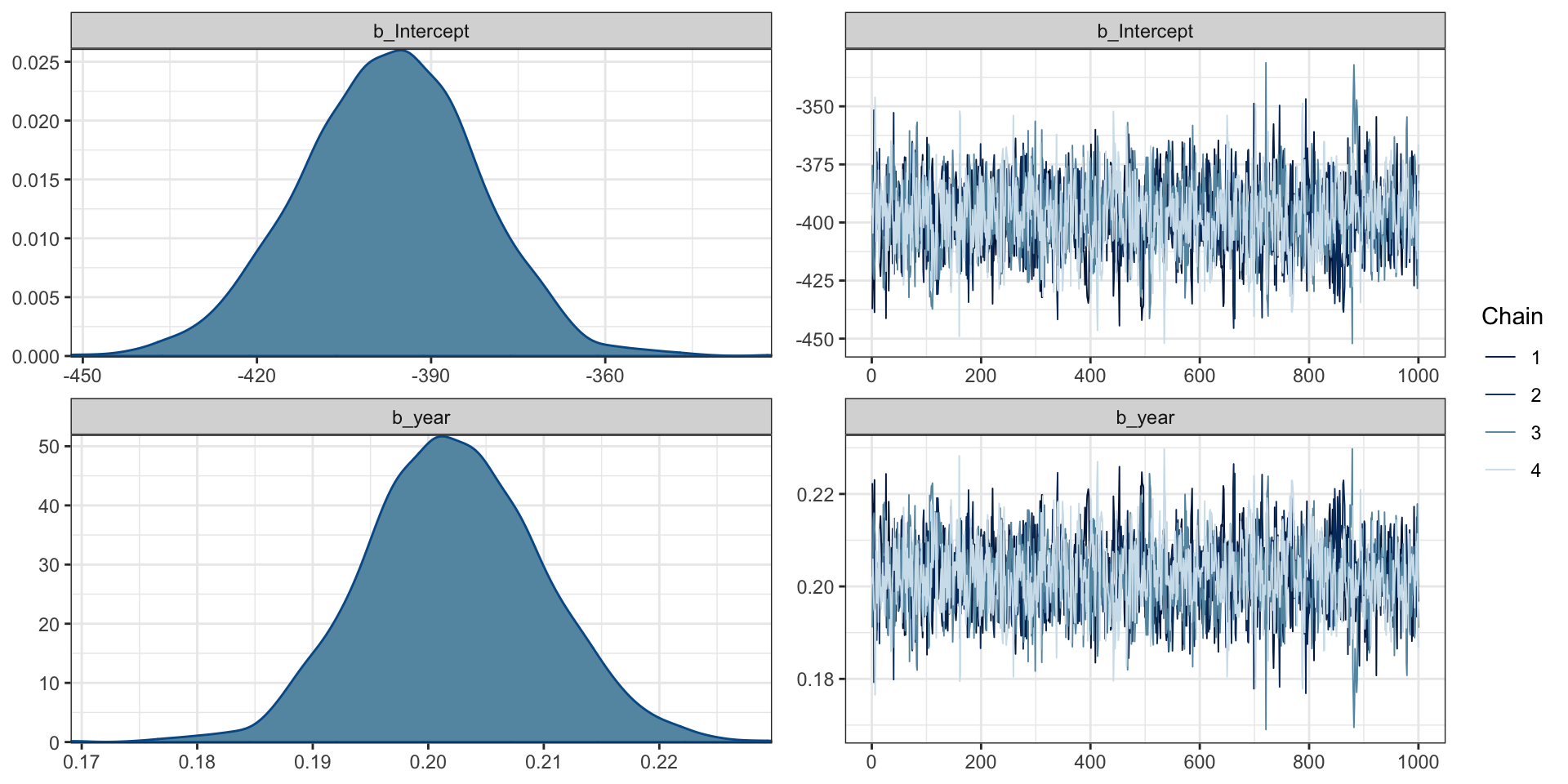
Bayesian Poisson Regression Model
Family: poisson
Links: mu = log
Formula: cases ~ year
Data: aids (Number of observations: 13)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -397.28 15.38 -427.88 -368.22 1.00 1568 1582
year 0.20 0.01 0.19 0.22 1.00 1569 1582
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).Model priors
MCMC Diagnostics
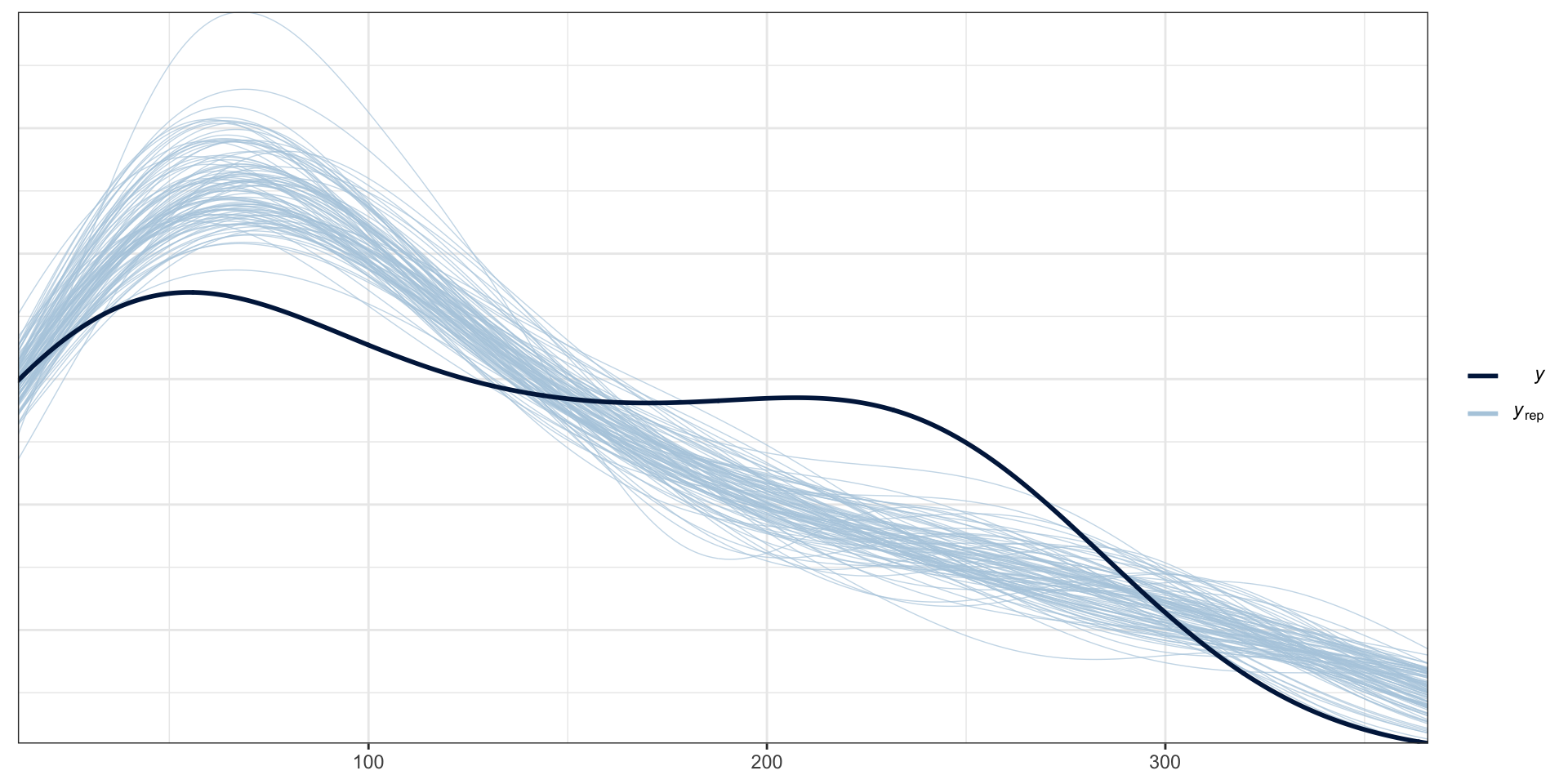
Posterior Predictive Check
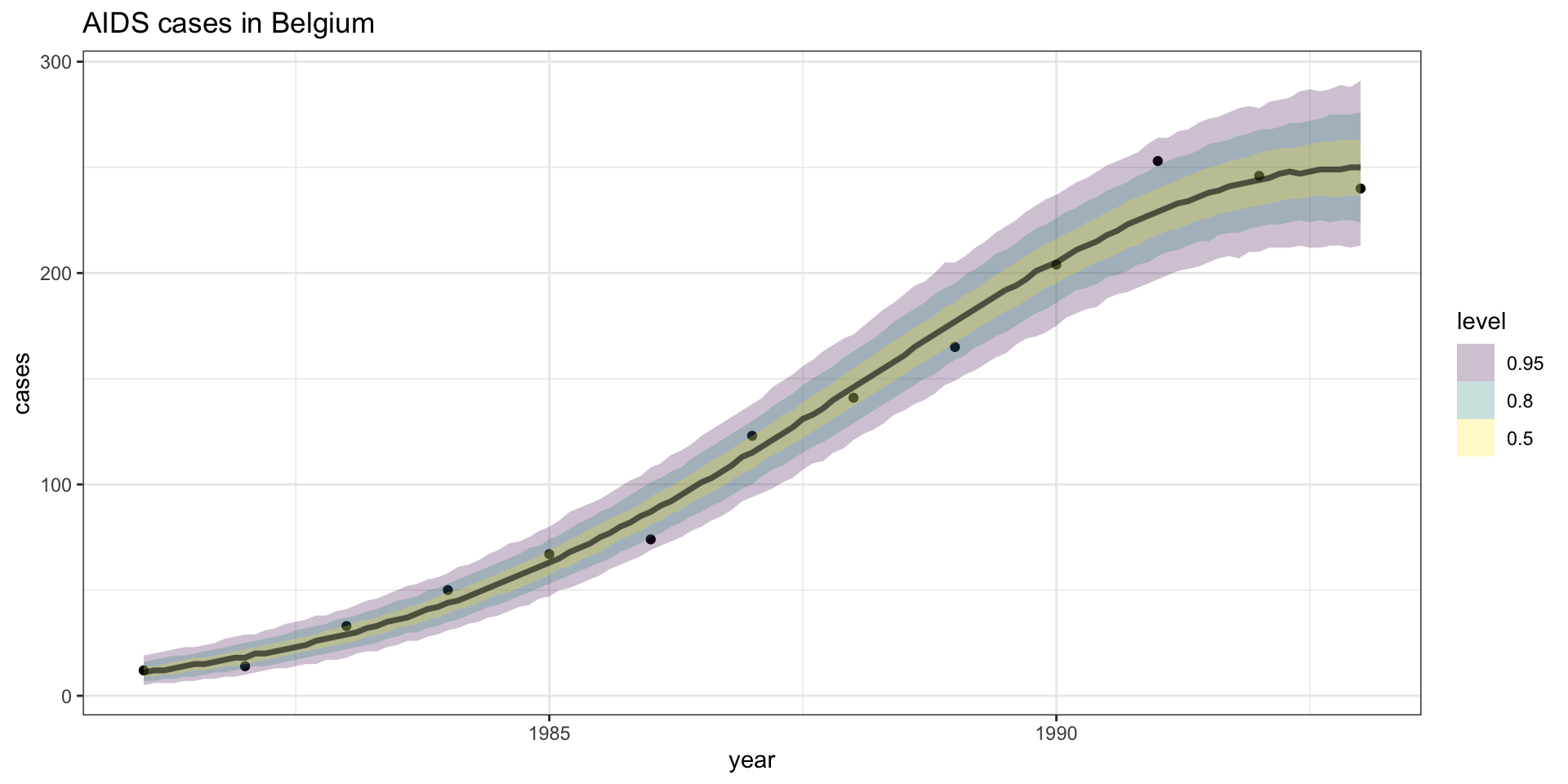
Model fit - \(\lambda\) CI
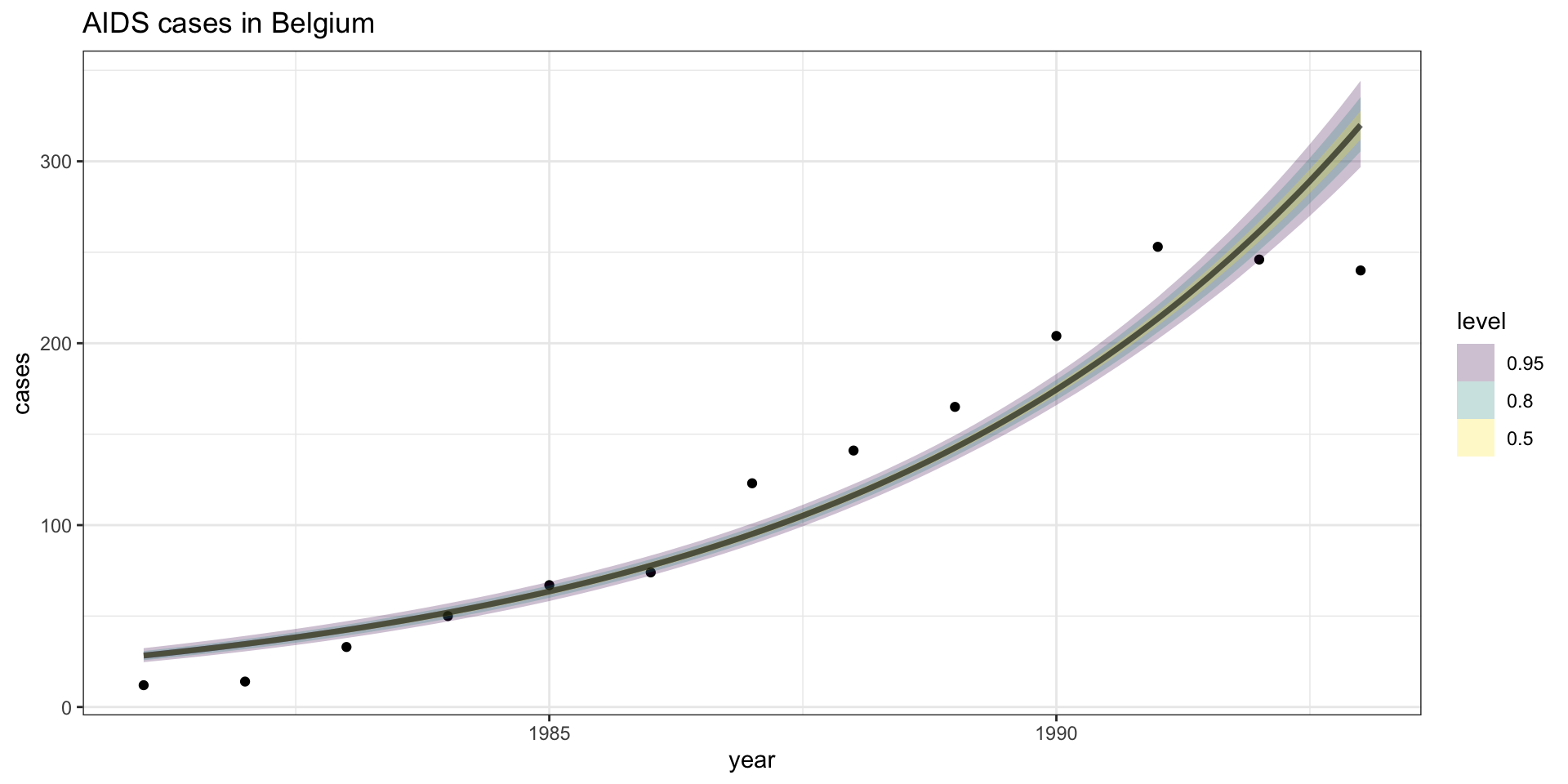
Model fit - \(Y\) CI
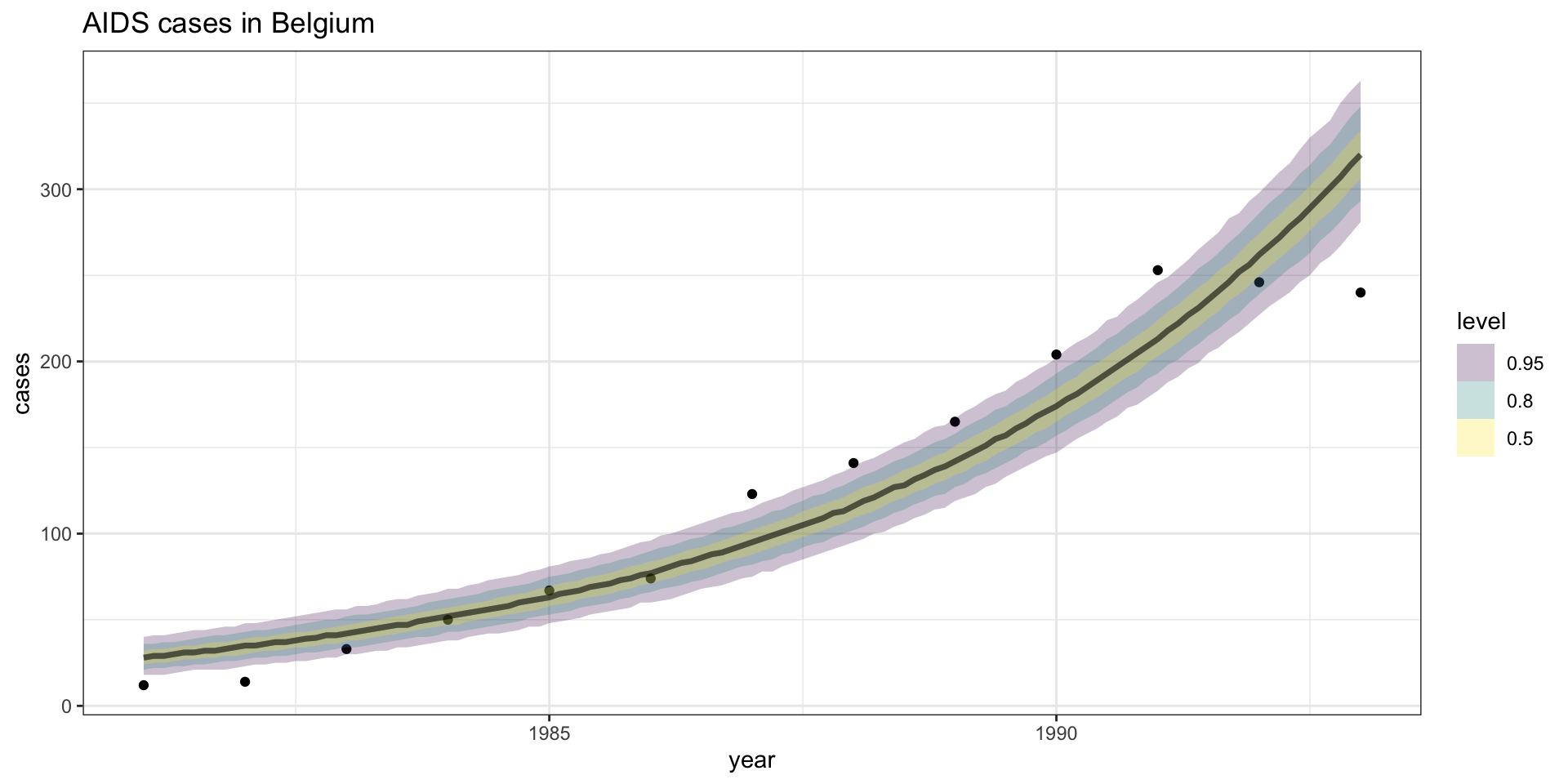
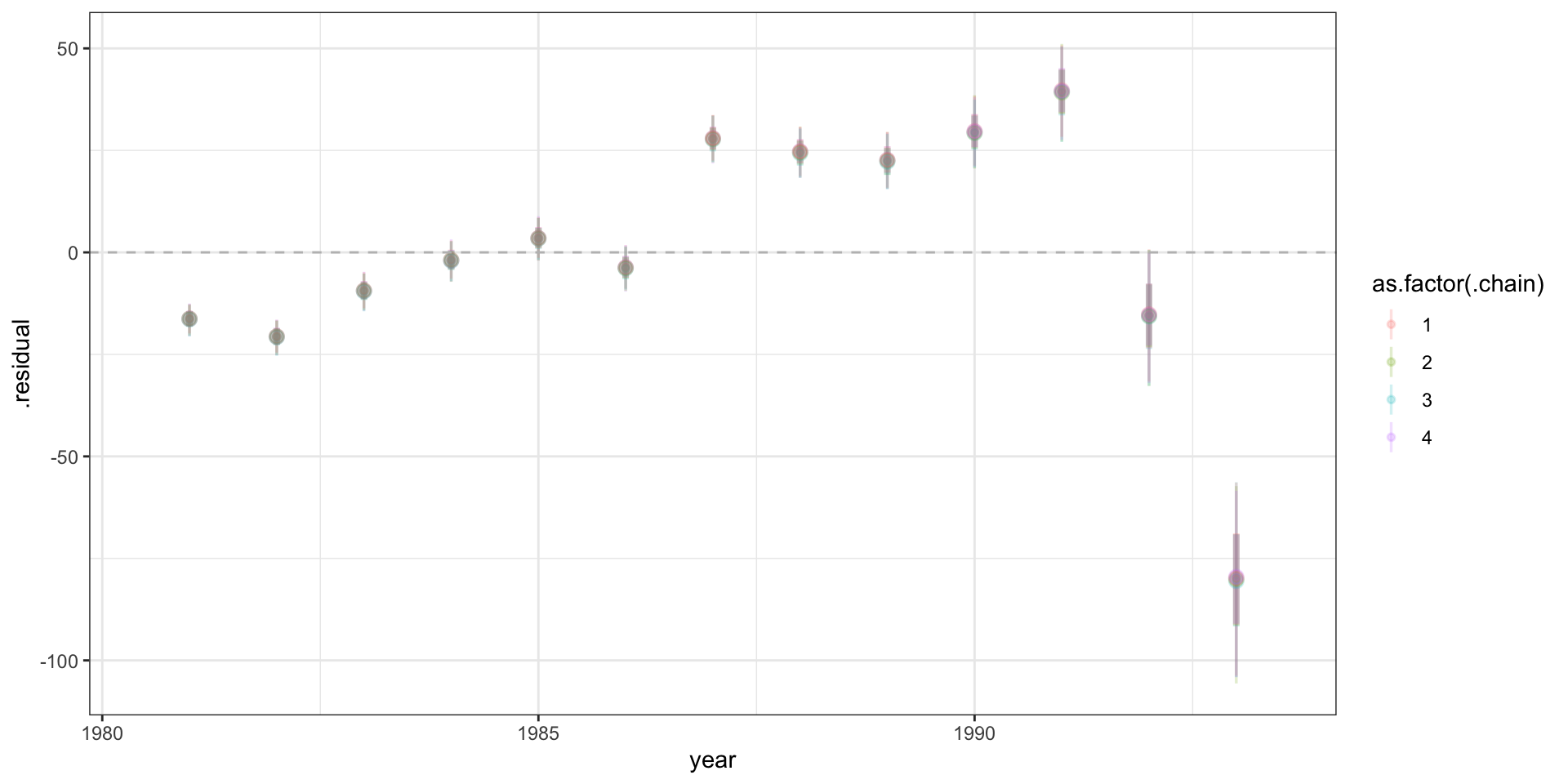
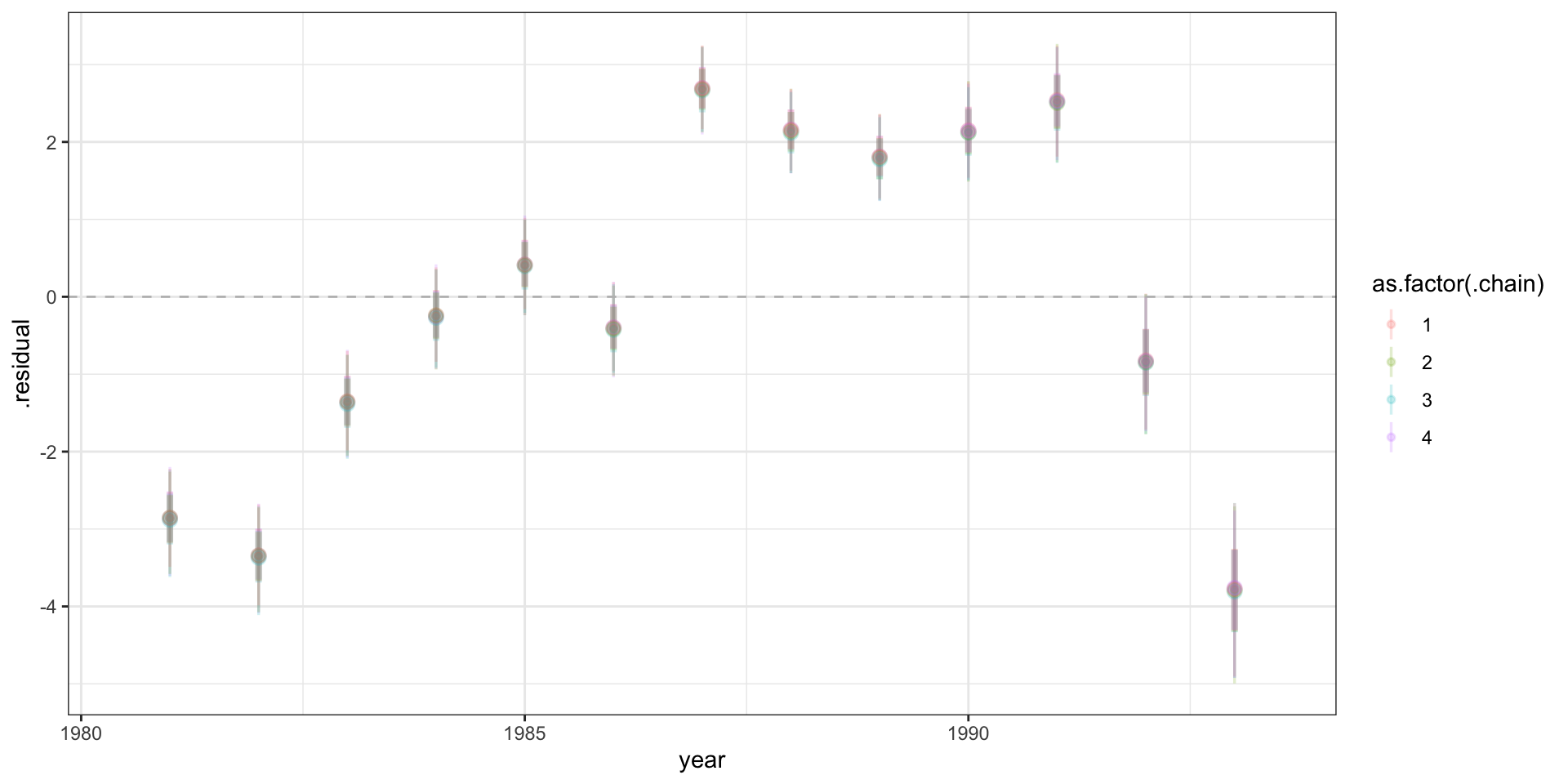
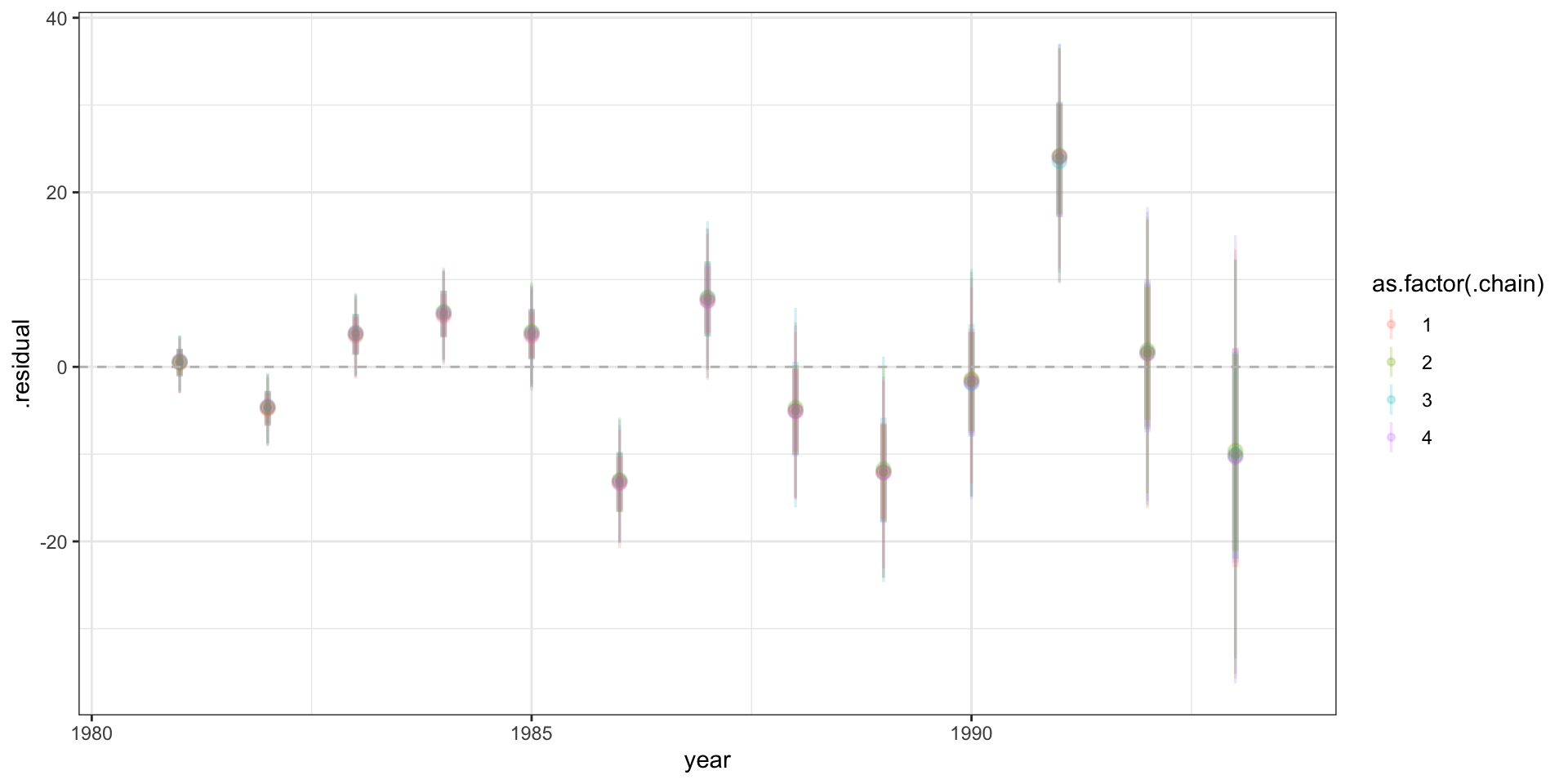
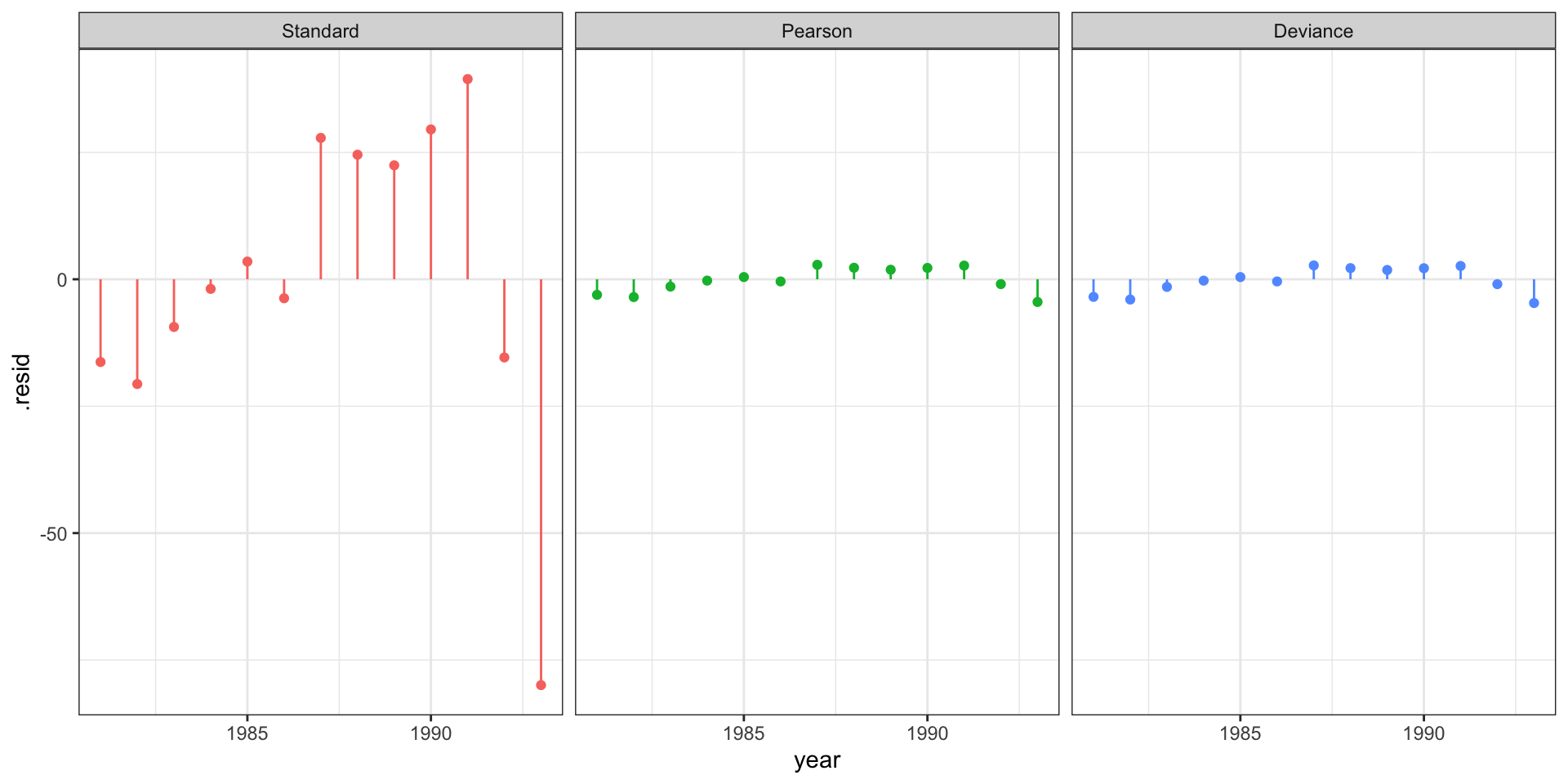
Residuals
# A tibble: 52,000 × 7
year cases .row .chain .iteration .draw .residual
<int> <int> <int> <int> <int> <int> <dbl>
1 1981 12 1 1 1 1 -11.4
2 1981 12 1 1 2 2 -14.0
3 1981 12 1 1 3 3 -13.1
4 1981 12 1 1 4 4 -12.2
5 1981 12 1 1 5 5 -12.0
6 1981 12 1 1 6 6 -19.8
7 1981 12 1 1 7 7 -18.7
8 1981 12 1 1 8 8 -18.7
9 1981 12 1 1 9 9 -20.3
10 1981 12 1 1 10 10 -19.5
# … with 51,990 more rowsResidual plot
Standardized residuals?
Model performance - rmse, crps
predicted_draws_fix(g_bayes, newdata = aids) |>
group_by(.chain, .row) |>
summarize(
rmse = yardstick::rmse_vec(cases, .prediction),
crps = calc_crps(.prediction, cases)
) |>
group_by(.chain) |>
summarize(
rmse = mean(rmse),
crps = mean(crps)
)# A tibble: 4 × 3
.chain rmse crps
<int> <dbl> <dbl>
1 1 26.3 17.7
2 2 26.1 17.5
3 3 26.3 17.7
4 4 26.3 17.8Model performance - emp coverage
predicted_draws_fix(g_bayes, newdata = aids) |>
group_by(.row, cases) |>
tidybayes::mean_hdi(
.prediction, .width = c(0.5,0.9,0.95)
) |>
mutate(contains = cases >= .lower & cases <= .upper) %>%
group_by(.width) |>
summarize(
emp_cov = sum(contains)/n()
)# A tibble: 3 × 2
.width emp_cov
<dbl> <dbl>
1 0.5 0.154
2 0.9 0.385
3 0.95 0.462Updating the model
Quadratic fit
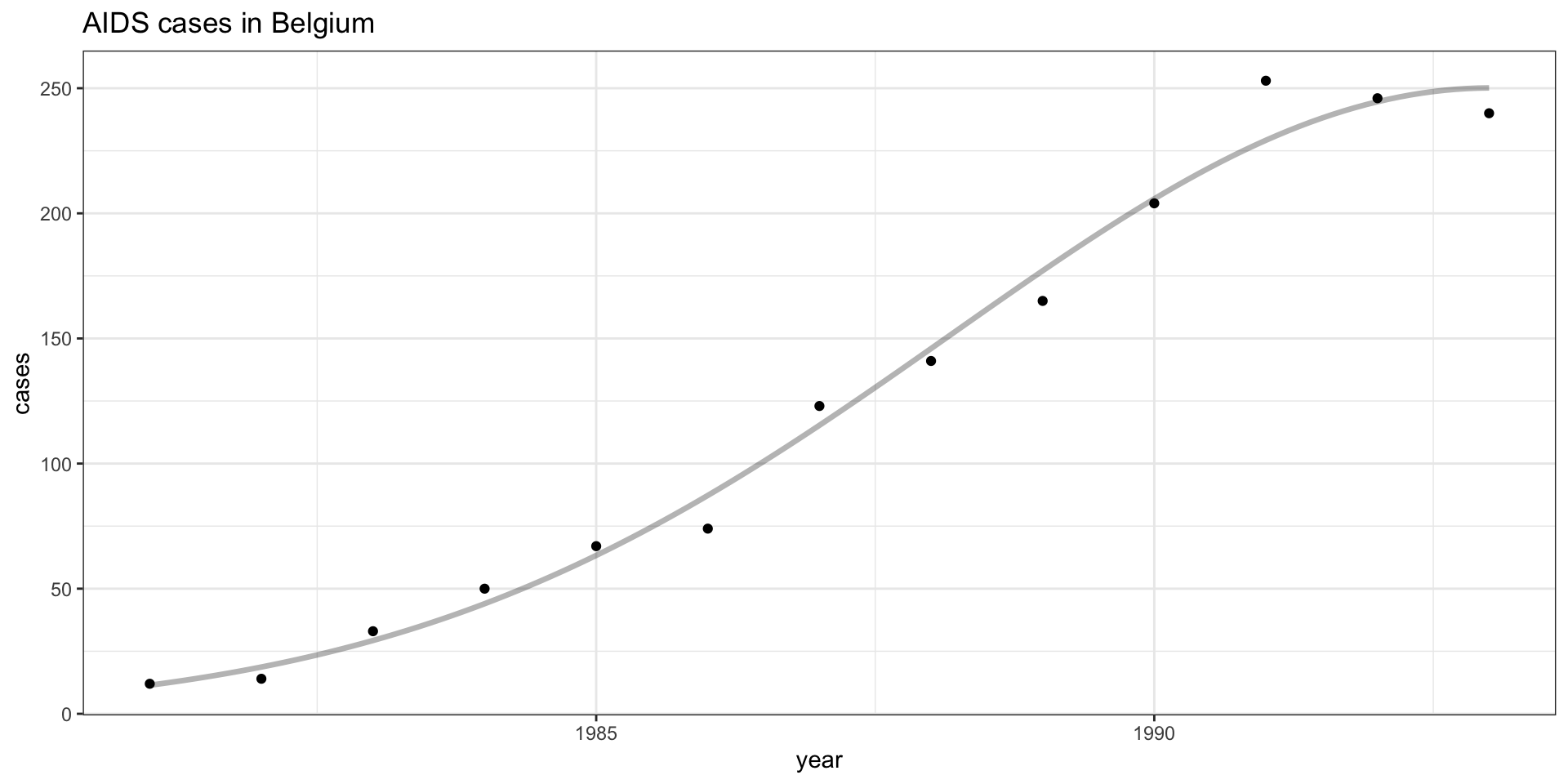
Quadratic fit - residuals
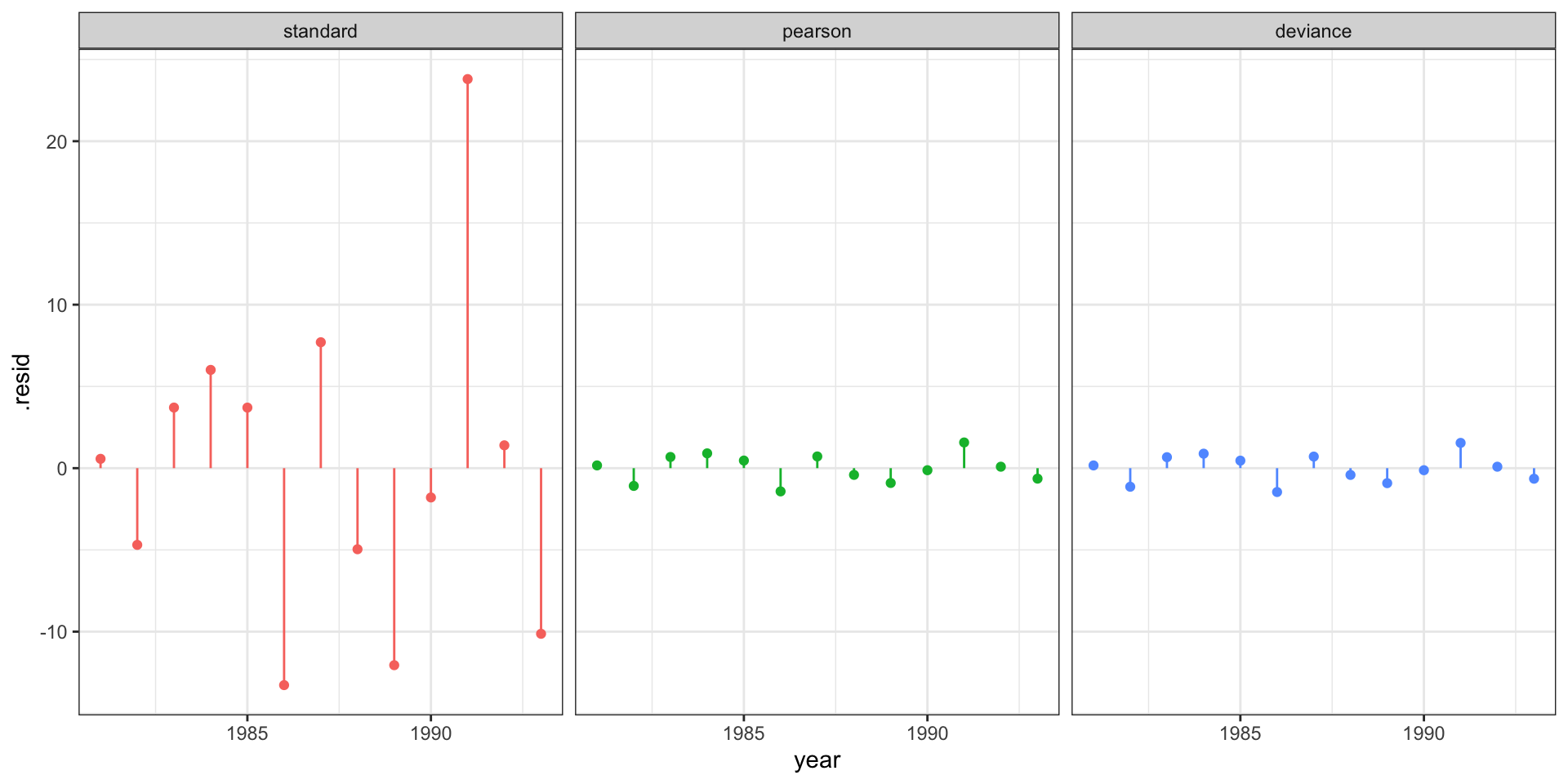
Bayesian quadratic fit
Family: poisson
Links: mu = log
Formula: cases ~ year + I(year^2)
Data: aids (Number of observations: 13)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -8538.33 15758.51 -35873.48 1378.93 3.72 4 11
year -0.23 1.21 -1.59 1.32 3.73 4 11
IyearE2 0.00 0.00 -0.00 0.01 3.56 4 11
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).Diagnostics
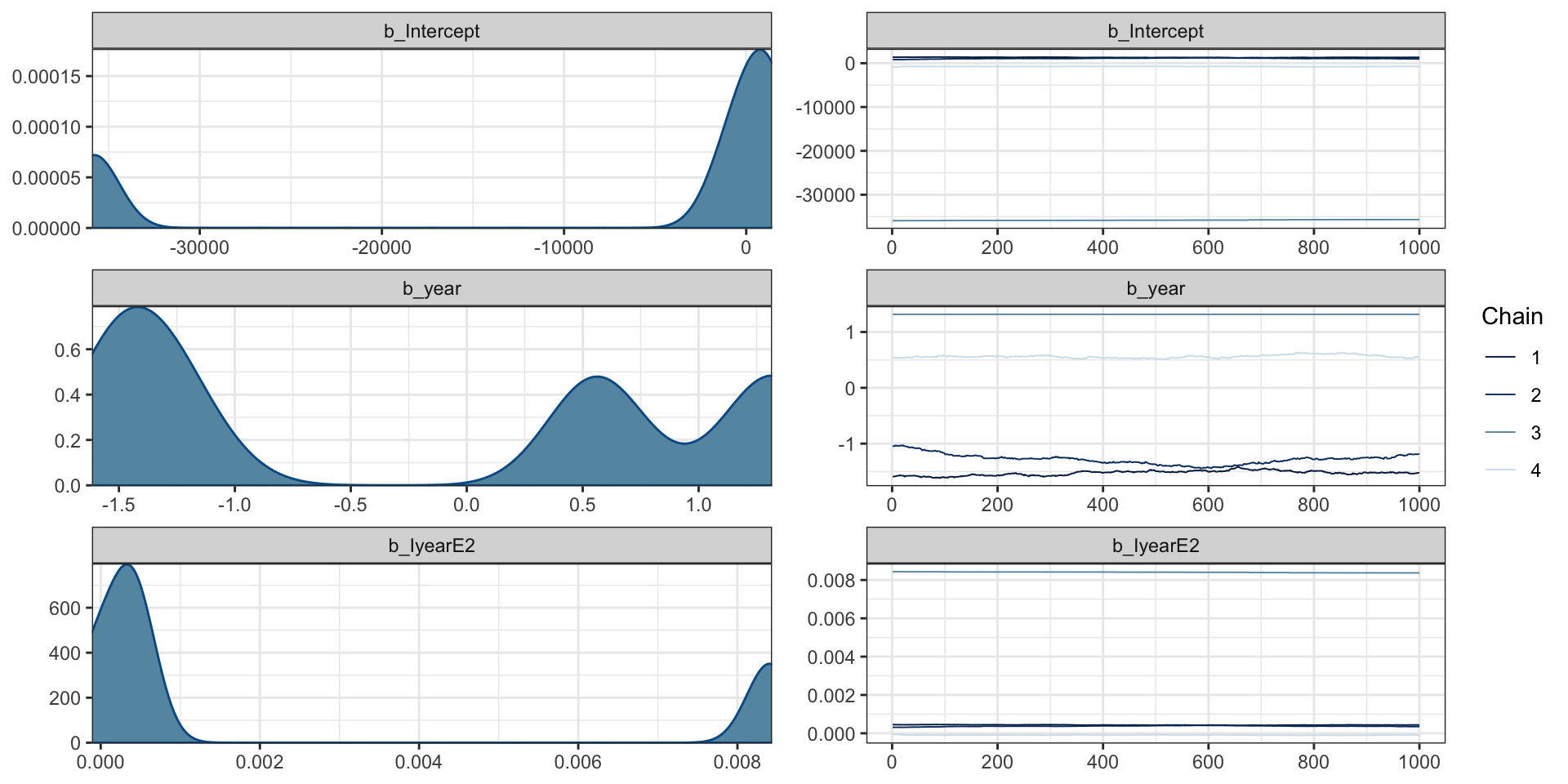
Bayesian quadratic fit (fixed)
Family: poisson
Links: mu = log
Formula: cases ~ I(year - min(year)) + I((year - min(year))^2)
Data: aids (Number of observations: 13)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 2.43 0.14 2.14 2.70 1.00 1012 1259
IyearMminyear 0.51 0.04 0.44 0.59 1.00 1079 1342
IyearMminyearE2 -0.02 0.00 -0.03 -0.02 1.00 1180 1408
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).Diagnostics
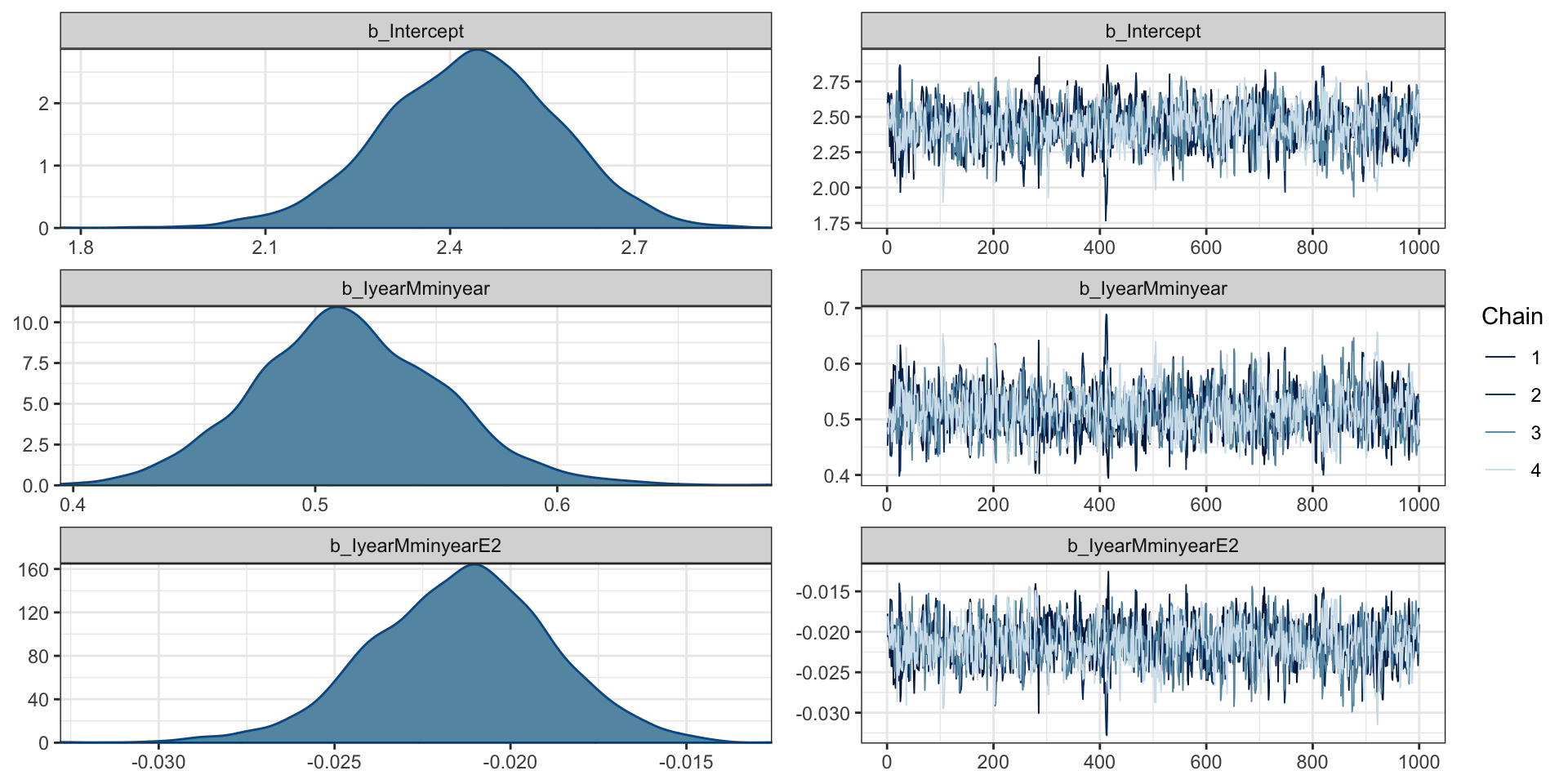
PP Checks
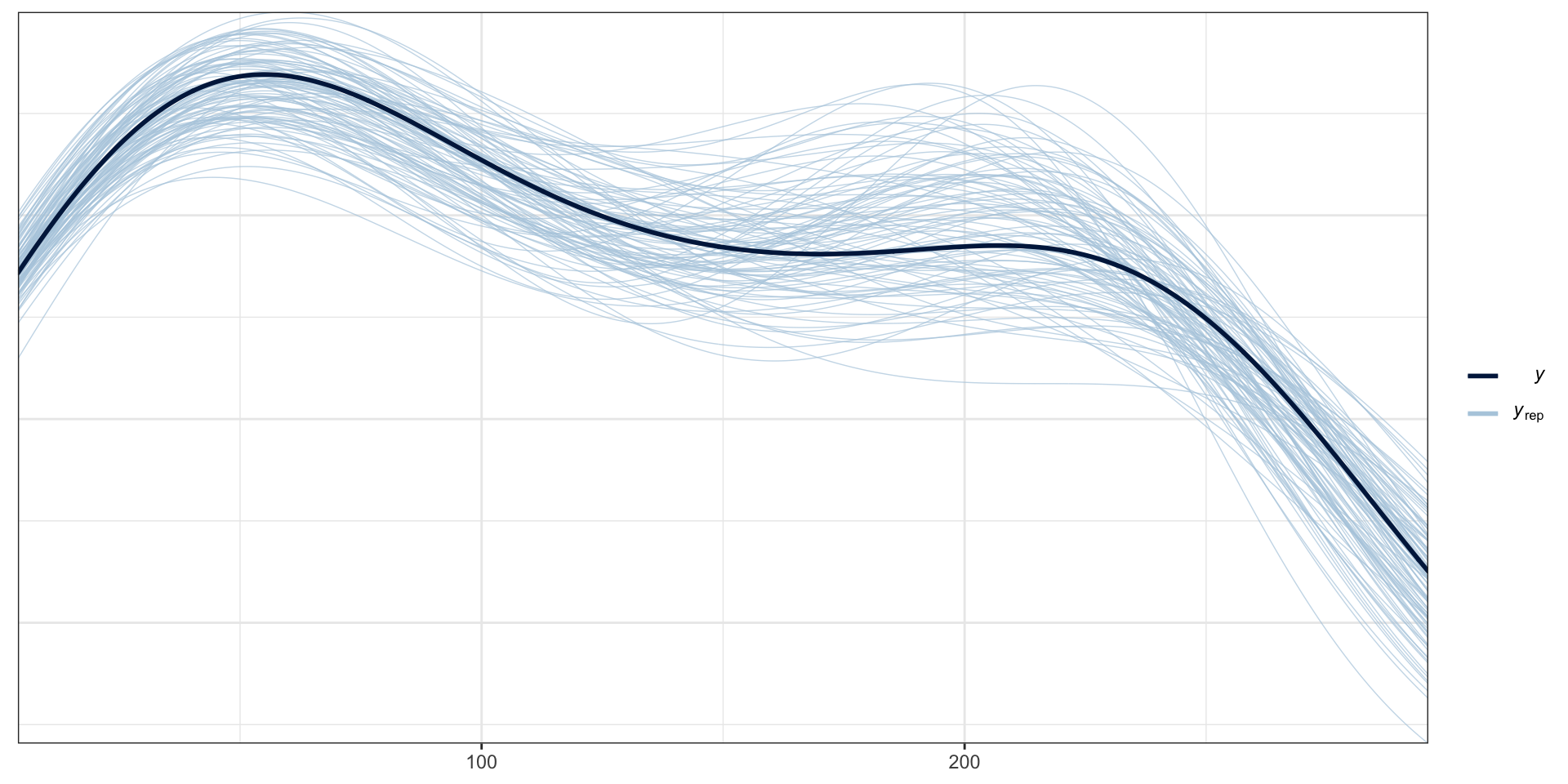
Model fit - \(Y\) CI
Residuals
Model performance - rmse, crps
predicted_draws_fix(g2_bayes, newdata = aids) |>
group_by(.chain, .row) |>
summarize(
rmse = yardstick::rmse_vec(cases, .prediction),
crps = calc_crps(.prediction, cases)
) |>
group_by(.chain) |>
summarize(
rmse = mean(rmse),
crps = mean(crps)
)# A tibble: 4 × 3
.chain rmse crps
<int> <dbl> <dbl>
1 1 14.1 5.19
2 2 14.2 5.06
3 3 14.2 5.09
4 4 14.2 4.99Model performance - emp coverage
predicted_draws_fix(g2_bayes, newdata = aids) |>
group_by(.row, cases) |>
tidybayes::mean_hdi(
.prediction, .width = c(0.5,0.9,0.95)
) |>
mutate(contains = cases >= .lower & cases <= .upper) %>%
group_by(.width) |>
summarize(
emp_cov = sum(contains)/n()
)# A tibble: 3 × 2
.width emp_cov
<dbl> <dbl>
1 0.5 0.692
2 0.9 1
3 0.95 1 Logistic regression
Logistic regression as a GLM
This is another case of a generalized linear model, specifically where the outcome is 0-1 data (i.e. Bernoulli draws),
\[ \begin{aligned} Y_i &\sim \text{Bern}(p_i)\\ \text{logit} \, E(Y_i|\boldsymbol{X}_{i\cdot}) &= \text{logit}(p_i) = \underset{1 \times p}{\boldsymbol{X}_{i\cdot}}\underset{p \times 1}{\boldsymbol{\beta}} \\ \\ E(Y_i) &= p_i \\ Var(Y_i) &= p_i(1-p_i) \\ \\ \text{logit}(p_i) &= \log \frac{p_i}{1-p_i} \\ \text{logit}^{-1}(x) &= \frac{\exp(x)}{1+\exp(x)} = \frac{1}{1+\exp(-x)} \end{aligned} \]
Background
Next we’ll be looking at data on the presence and absence of the short-finned eel (Anguilla australis) at a number of sites in New Zealand.
These data come from
- Leathwick, J. R., Elith, J., Chadderton, W. L., Rowe, D. and Hastie, T. (2008), Dispersal, disturbance and the contrasting biogeographies of New Zealand’s diadromous and non-diadromous fish species. Journal of Biogeography, 35: 1481–1497.

Species Distribution
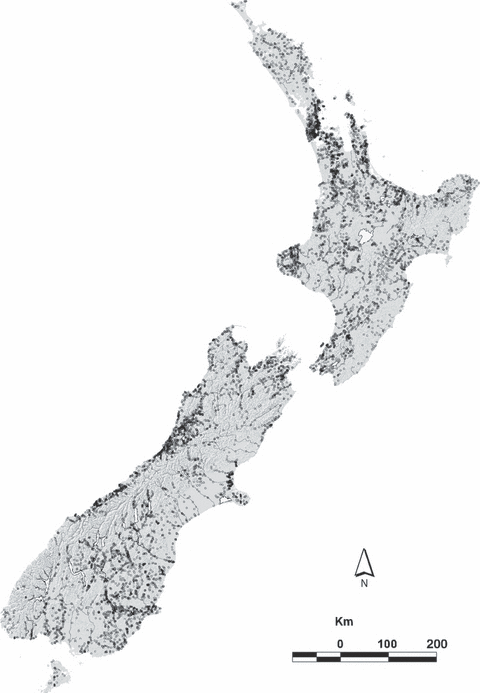
Codebook:
presence- presence (1) or absence (0) of Anguilla australis at the sampling locationSegSumT- Summer air temperature (degrees C)DSDist- Distance to coast (km)DSMaxSlope- Maximum downstream slope (degrees)USRainDays- days per month with rain greater than 25 mmUSSlope- average slope in the upstream catchment (degrees)USNative- area with indigenous forest (proportion)DSDam- Presence of known downstream obstructions, mostly damsMethod- fishing method (electric,net,spot,trap, ormixture)LocSed- weighted average of proportional cover of bed sediment- mud
- sand
- fine gravel
- coarse gravel
- cobble
- boulder
- bedrock
Data
# A tibble: 824 × 10
presence SegSumT DSDist DSMaxSl…¹ USRai…² USSlope USNat…³ DSDam Method LocSed
<int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <fct> <dbl>
1 0 16 50.2 0.57 2.47 9.8 0.81 0 elect… 4.8
2 1 18.7 133. 1.15 1.15 8.3 0.34 0 elect… 2
3 0 18.3 107. 0.57 0.847 0.4 0 0 spo 1
4 0 16.7 167. 1.72 0.21 0.4 0.22 1 elect… 4
5 1 17.2 3.95 1.15 1.98 21.9 0.96 0 elect… 4.7
6 0 15.1 11.2 1.72 3.3 25.7 1 0 elect… 4.5
7 0 12.7 42.4 2.86 0.43 9.6 0.09 0 elect… 4.3
8 1 18.2 94.4 3.43 0.847 20.5 0.92 0 elect… 3.6
9 0 14.9 45.7 2.29 2.25 3.9 0.38 0 elect… 3.7
10 1 18.3 91.9 1.72 0.861 6.7 0.58 1 elect… 1
# … with 814 more rows, and abbreviated variable names ¹DSMaxSlope,
# ²USRainDays, ³USNativeTest / train split
EDA
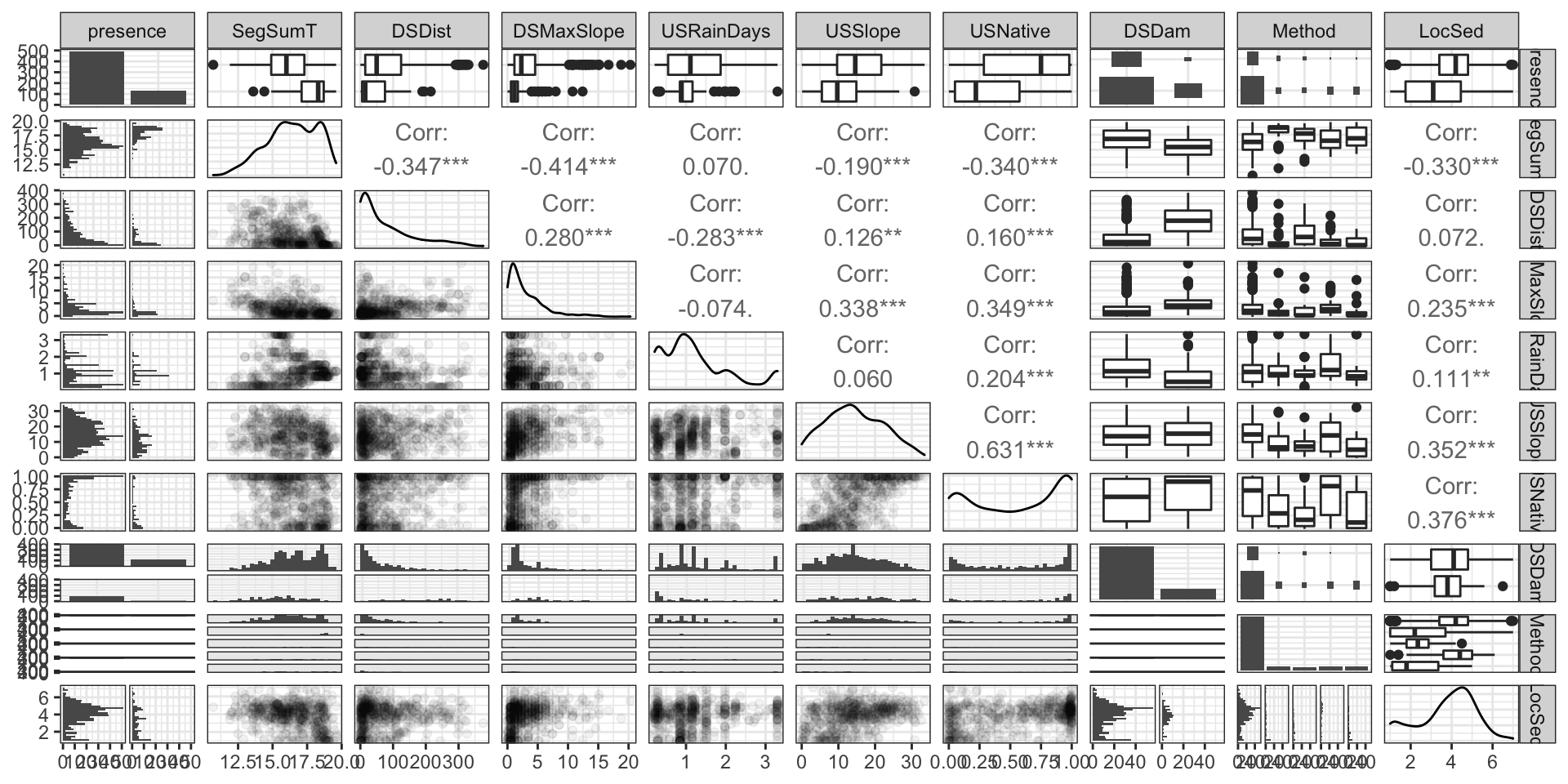
EDA (part 1)
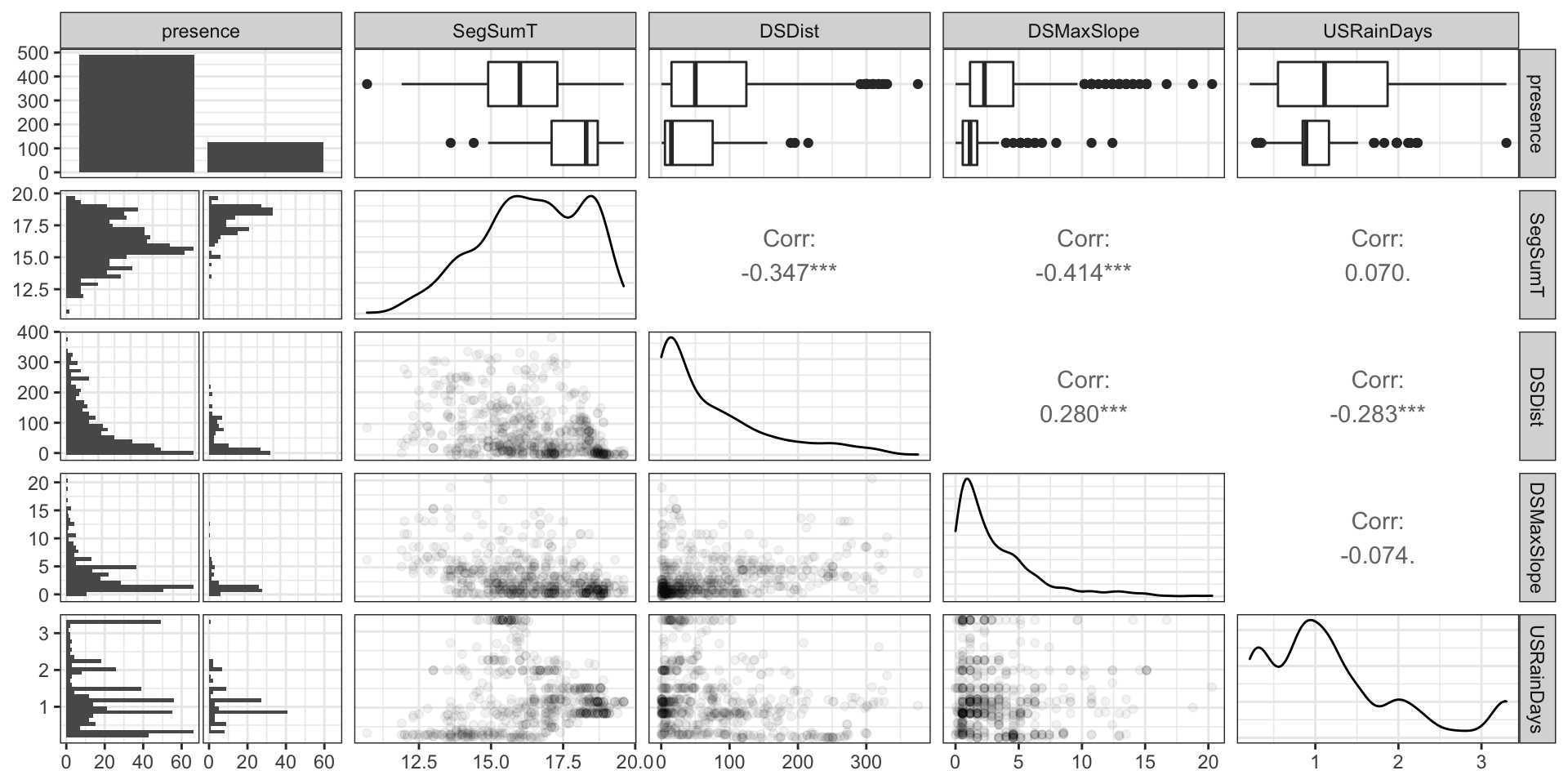
EDA (part 2)
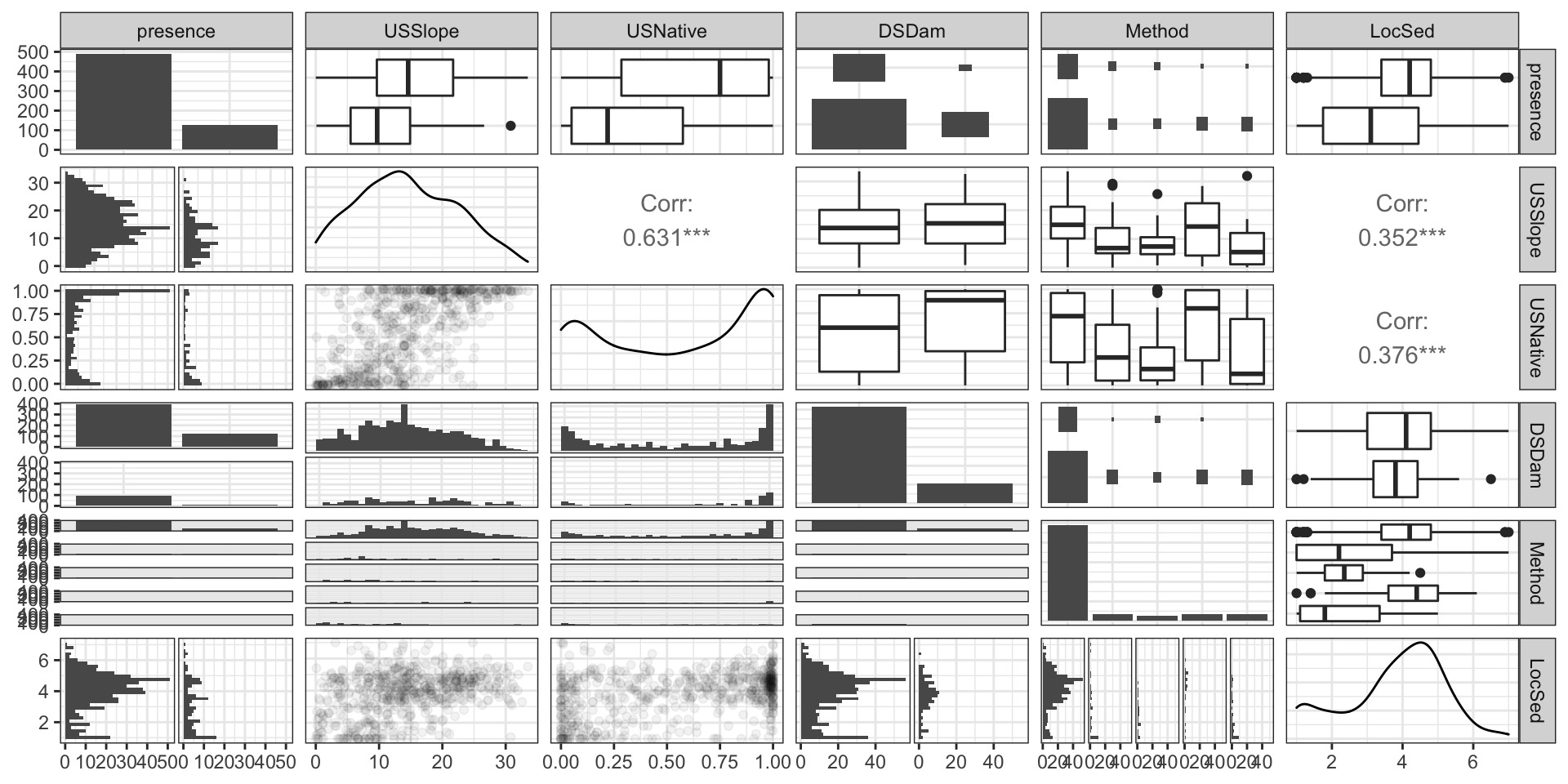
EDA (part 3)
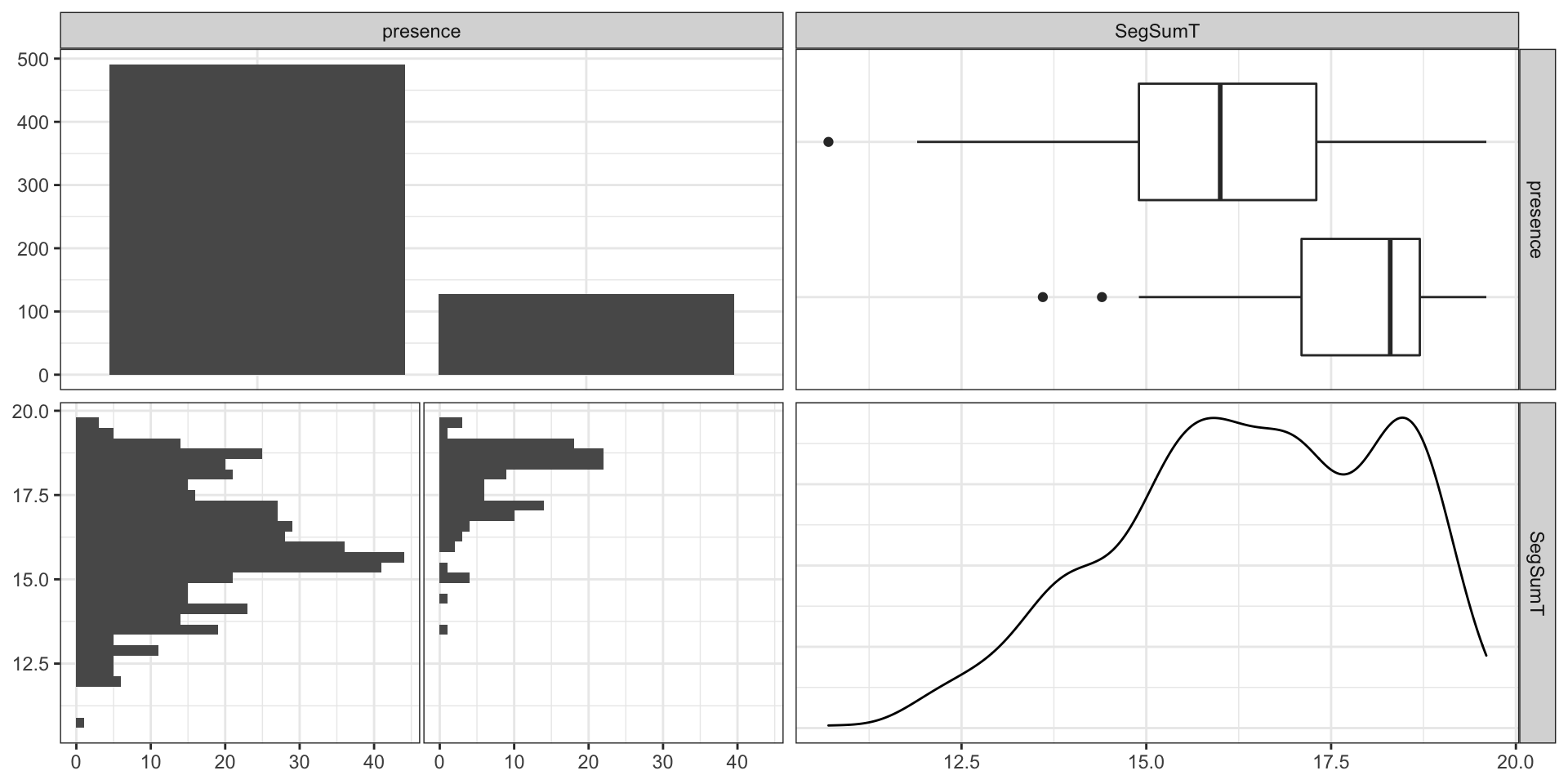
Basic Model
Model
Call:
glm(formula = presence ~ SegSumT, family = binomial, data = anguilla_train)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.4707 -0.6598 -0.3759 -0.1417 2.8815
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -15.02201 1.53770 -9.769 <2e-16 ***
SegSumT 0.80047 0.08726 9.173 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 627.81 on 617 degrees of freedom
Residual deviance: 501.93 on 616 degrees of freedom
AIC: 505.93
Number of Fisher Scoring iterations: 5Fit
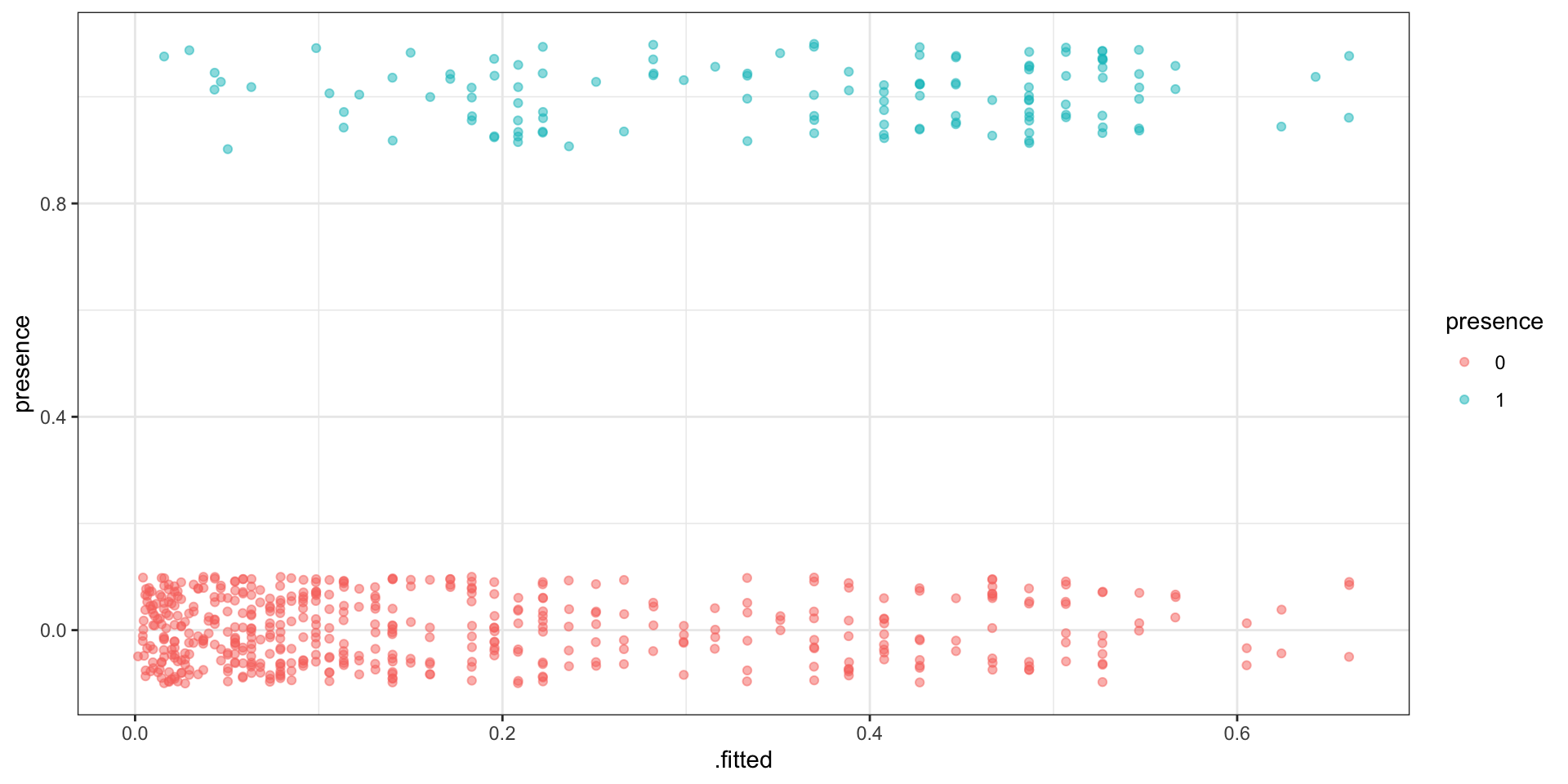
# A tibble: 618 × 8
presence SegSumT .fitted .resid .std.resid .hat .sigma .cooksd
<int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 16.4 0.131 -0.529 -0.530 0.00260 0.903 0.000197
2 1 17.1 0.209 1.77 1.77 0.00232 0.901 0.00443
3 0 14 0.0216 -0.209 -0.209 0.00231 0.903 0.0000256
4 0 18.2 0.389 -0.992 -0.994 0.00364 0.903 0.00117
5 0 15.6 0.0735 -0.391 -0.391 0.00286 0.903 0.000114
6 0 18.3 0.408 -1.02 -1.03 0.00395 0.902 0.00137
7 0 18.5 0.447 -1.09 -1.09 0.00466 0.902 0.00190
8 0 16.2 0.114 -0.491 -0.492 0.00270 0.903 0.000174
9 0 18 0.351 -0.930 -0.932 0.00313 0.903 0.000853
10 1 17.3 0.236 1.70 1.70 0.00233 0.901 0.00379
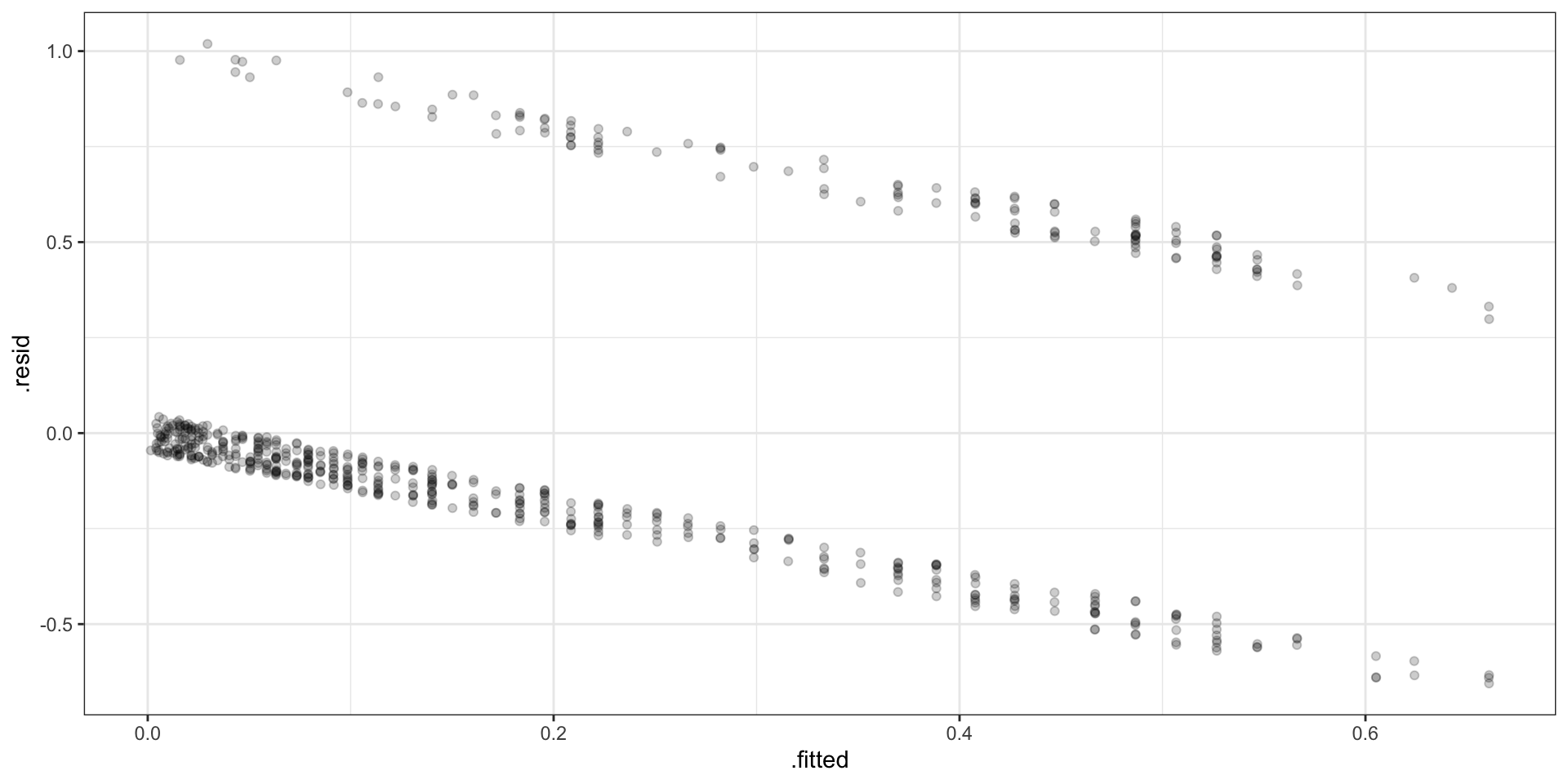
# … with 608 more rowsVisually
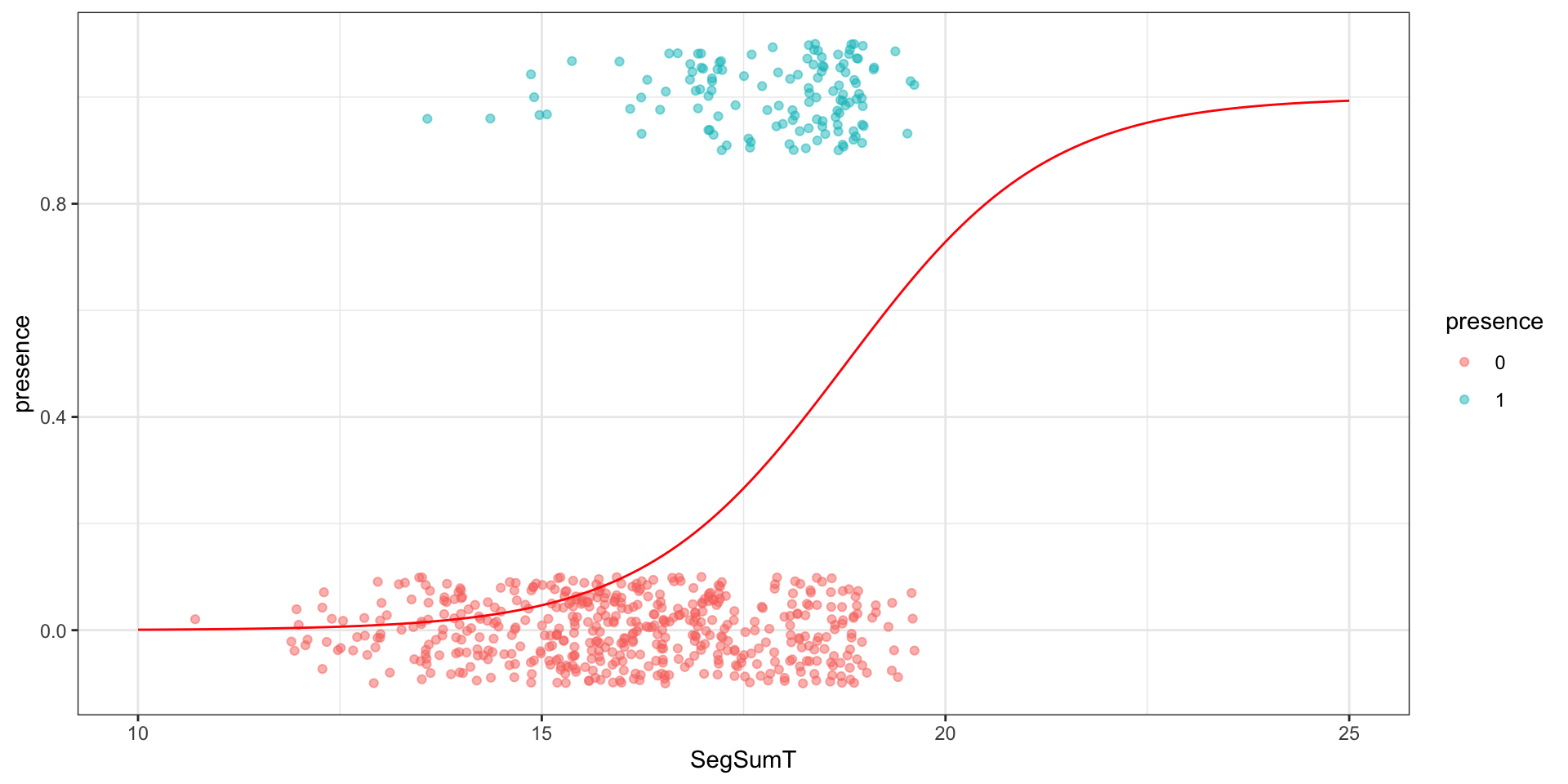
Separation
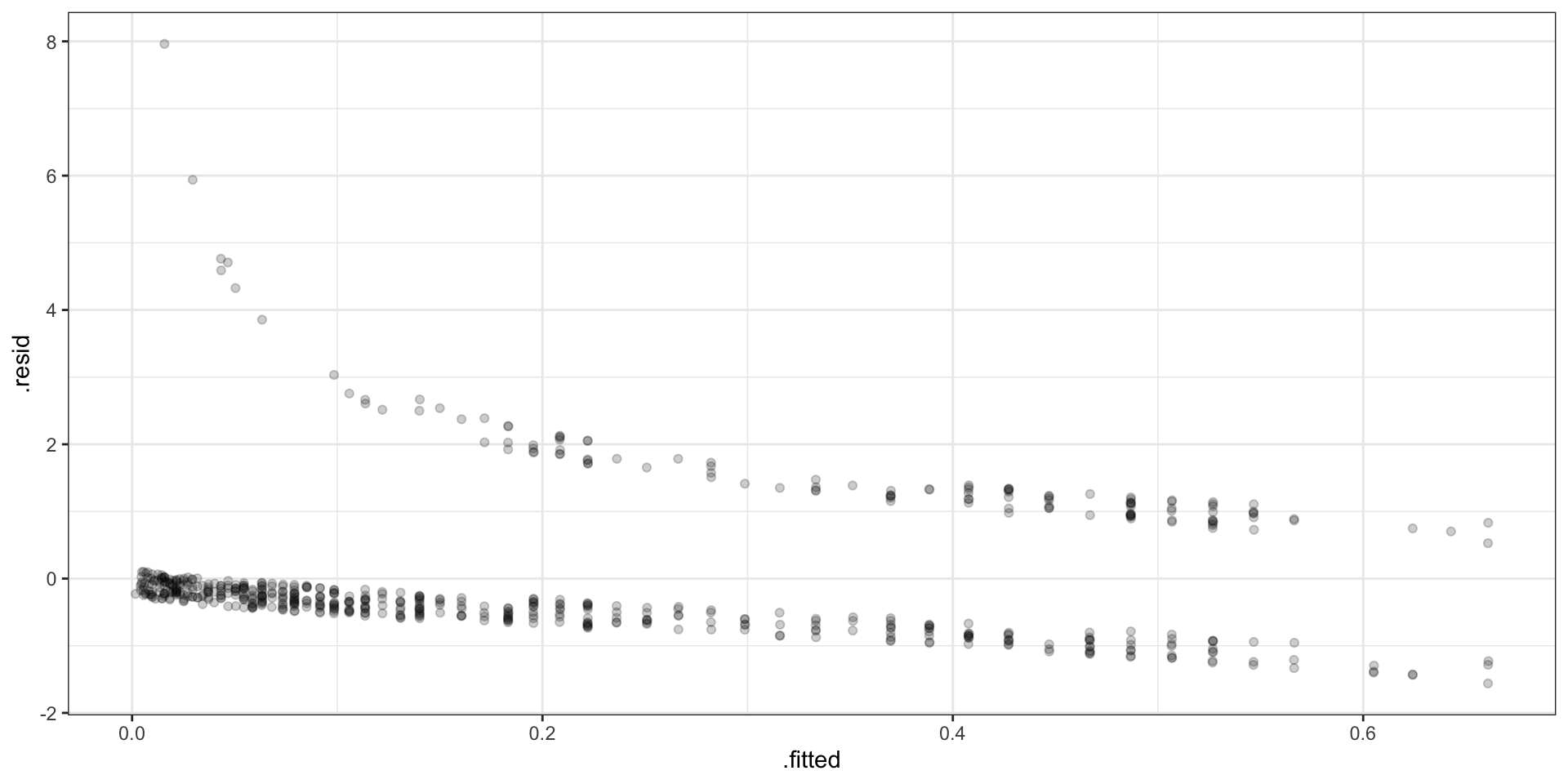
Standard Residuals
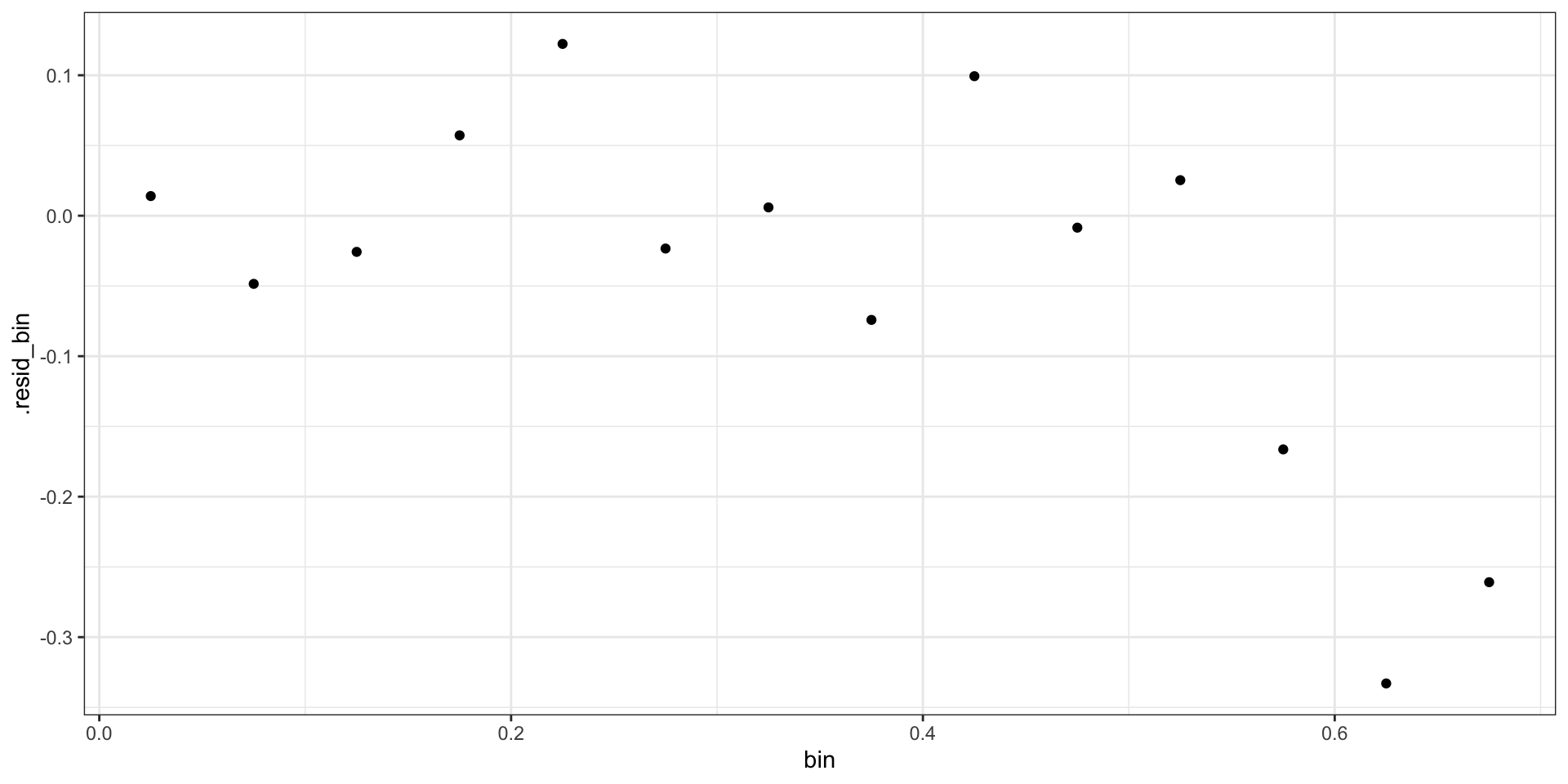
Binned Residuals
Pearson Residuals
\[ r_i = \frac{Y_i - E(Y_i)}{\sqrt{Var(Y_i)}} = \frac{Y_i - \hat{p}_i}{\sqrt{\hat{p}_i(1-\hat{p}_i)}} \]
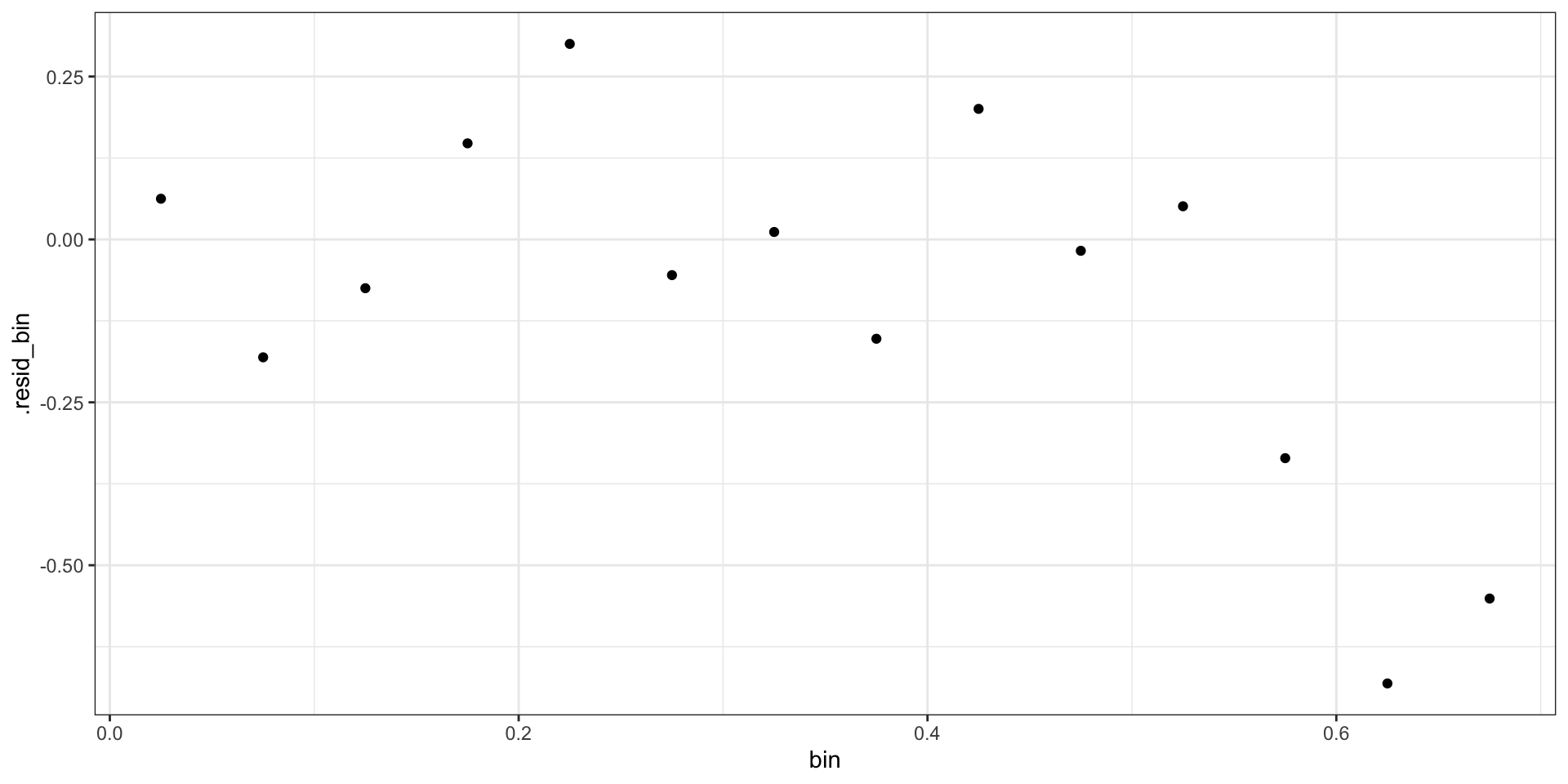
Binned Pearson Residuals
Deviance Residuals
\[ \begin{aligned} d_i = &\text{sign}(Y_i-\hat{p_i}) \, \times \\ &\sqrt{ -2 \left(Y_i \log \hat{p}_i+(1-Y_i)\log (1 - \hat{p}_i) \right) } \end{aligned} \]
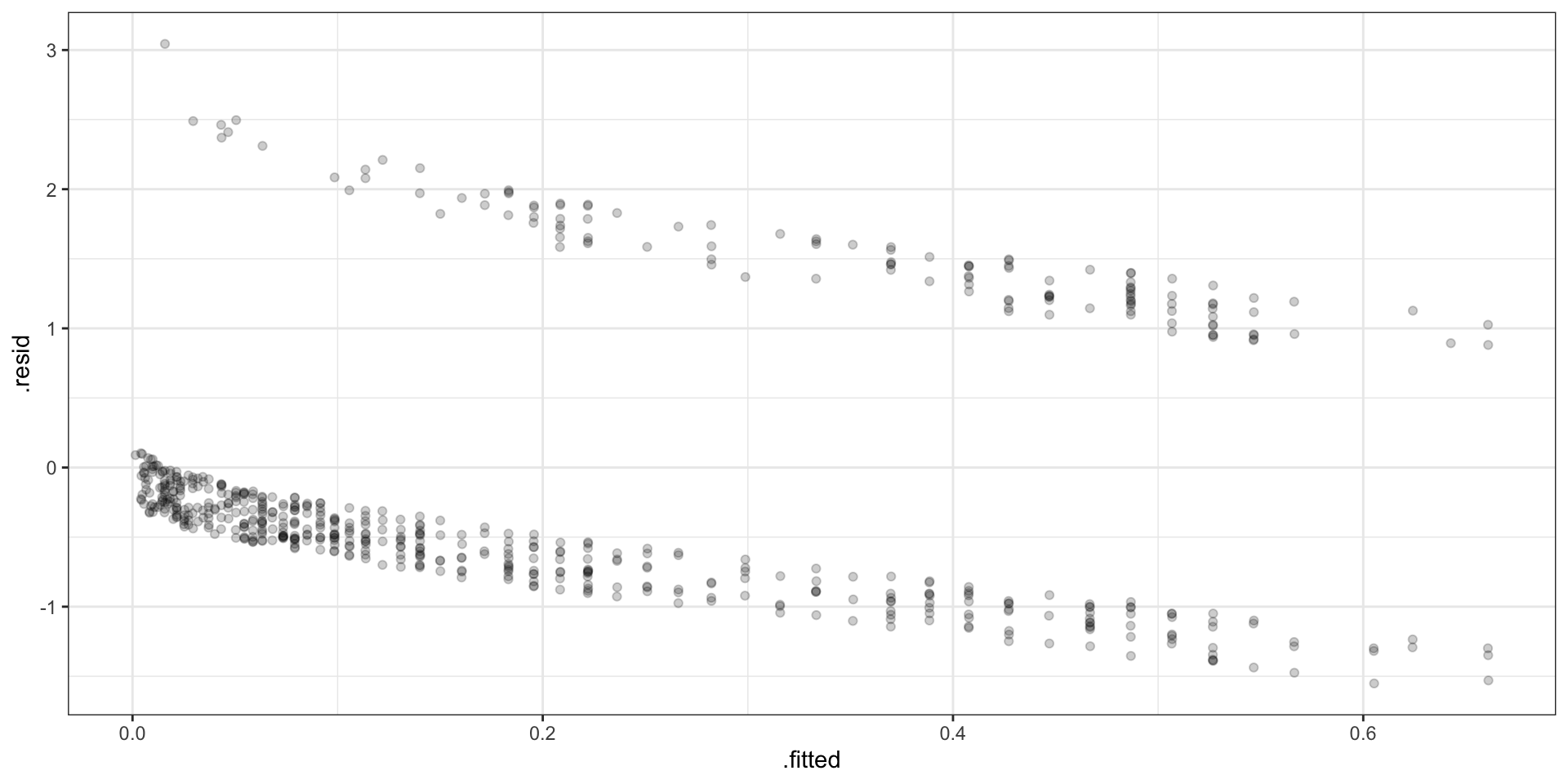
Binned Deviance Residuals
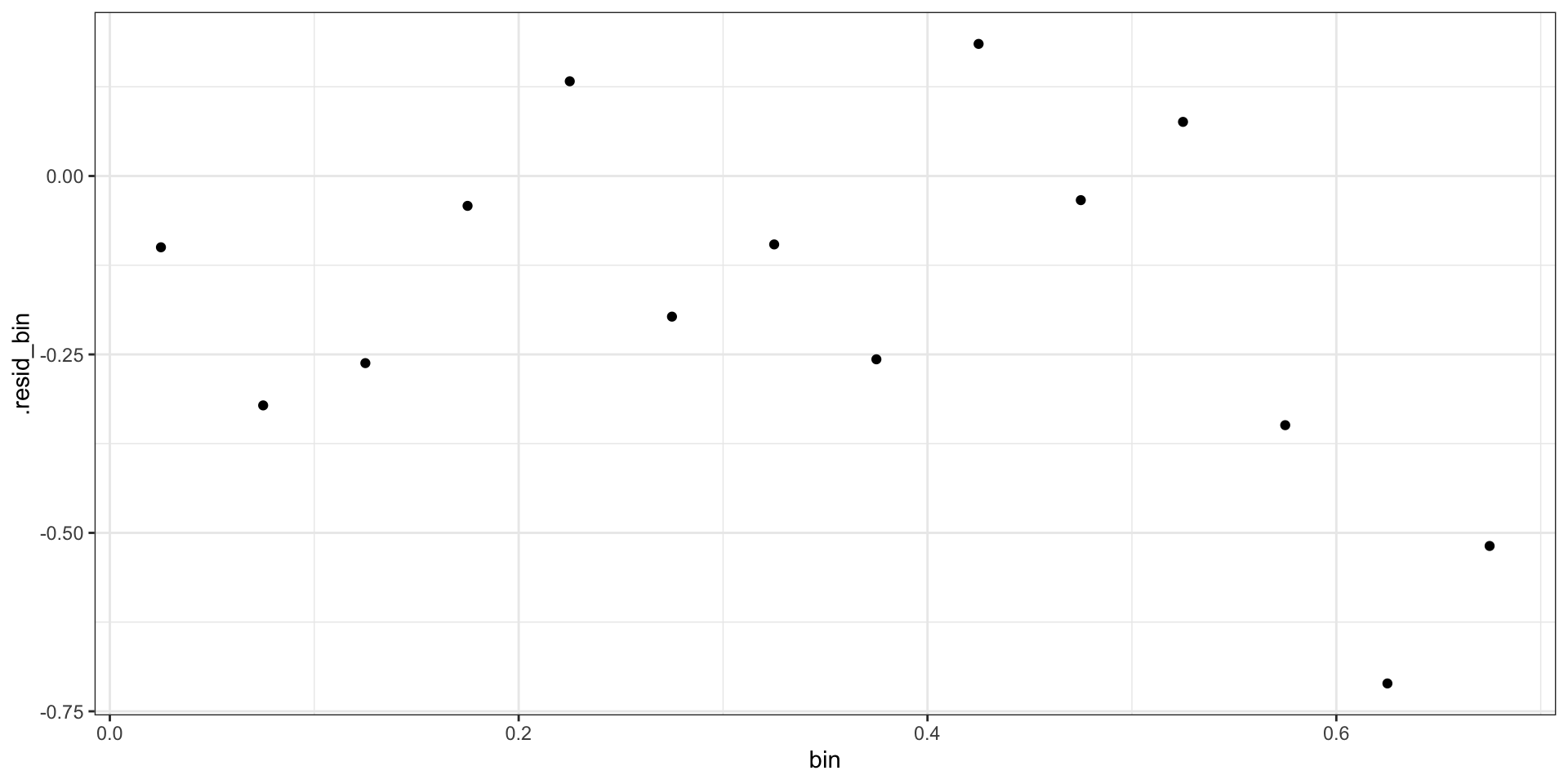
Checking Deviance
Call: glm(formula = presence ~ SegSumT, family = binomial, data = anguilla_train)
Coefficients:
(Intercept) SegSumT
-15.0220 0.8005
Degrees of Freedom: 617 Total (i.e. Null); 616 Residual
Null Deviance: 627.8
Residual Deviance: 501.9 AIC: 505.9Sta 344 - Fall 2022