Residual Analysis + Generalized Linear Models

Lecture 04

Dr. Colin Rundel

Lecture 3 wrap up

Where we left it - Empirical Coverage (\(\hat{y}\))

( epred_draws_fix(b, newdata=d) %>%
    group_by(x, y) %>% 
    tidybayes::mean_hdi(
      .epred, .width = c(0.5,0.9,0.95)
    ) %>%
    mutate(contains = y >= .lower & y <= .upper) %>%
    group_by(prob = .width) %>%
    summarize(
      emp_cov = sum(contains)/n()
    )
)

# A tibble: 3 × 2
   prob emp_cov
  <dbl>   <dbl>
1  0.5     0.02
2  0.9     0.11
3  0.95    0.14

What went wrong?

epred_draws_fix(b, newdata=d) %>%
  ggplot(aes(x=x)) +
    tidybayes::stat_interval(alpha=0.3, aes(y=.epred, group=x)) +
    geom_point(data=d, aes(y=y))

The right predictions

predicted_draws_fix(b, newdata=d) %>%
  ggplot(aes(x=x)) +
    tidybayes::stat_interval(alpha=0.3, aes(y=.prediction, group=x)) +
    geom_point(data=d, aes(y=y))

Empirical Coverage (\(y\))

predicted_draws_fix(b, newdata=d) %>%
  group_by(x, y) %>% 
  tidybayes::mean_hdi(
    .prediction, .width = c(0.5,0.8,0.9,0.95)
  ) %>%
  mutate(contains = y >= .lower & y <= .upper) %>%
  group_by(prob = .width) %>%
  summarize(
    emp_cov = sum(contains)/n()
  )

# A tibble: 4 × 2
   prob emp_cov
  <dbl>   <dbl>
1  0.5     0.44
2  0.8     0.81
3  0.9     0.97
4  0.95    0.97

RMSE - \(y\) vs \(\hat{y}\)

epred_draws_fix(b, newdata=d) %>% 
  group_by(.iteration, .chain) %>%
  yardstick::rmse(truth = y, estimate = .epred) %>%
  ggplot(aes(x=.estimate, fill=as.factor(.chain))) +
    geom_density(alpha=0.2) +
    guides(fill="none")

predicted_draws_fix(b, newdata=d) %>%
  group_by(.iteration, .chain) %>%
  yardstick::rmse(truth = y, estimate = .prediction) %>%
  ggplot(aes(x=.estimate, fill=as.factor(.chain))) +
    geom_density(alpha=0.2)+
    guides(fill="none")

Residual Analysis

Atmospheric \(\text{CO}_2\) (ppm) from Mauna Loa

Where to start?

Well, it looks like stuff is going up on average …

l = lm(co2~date, data=mauna_loa)

and then?

Well there is some periodicity lets add the month …

ls = lm(.resid~month, data=mauna_loa_l)

and then and then?

There is still some long term trend in the data, maybe a fancy polynomial can help …

lsy = lm(.resid~poly(date,5), data=mauna_loa_ls)

Putting it all together …

l_comb = lm(co2~date + month + poly(date,5), data=mauna_loa)
summary(l_comb)

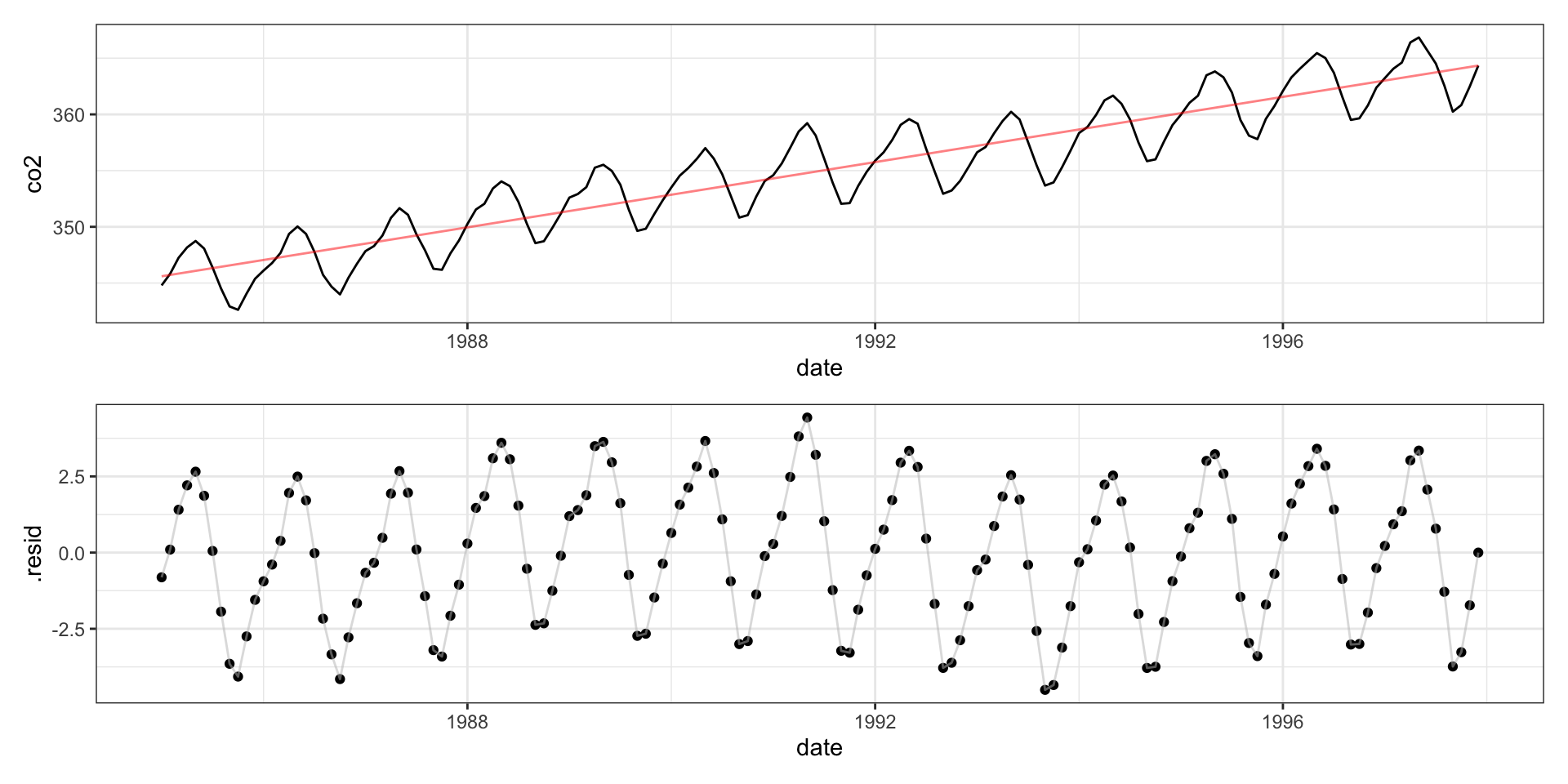
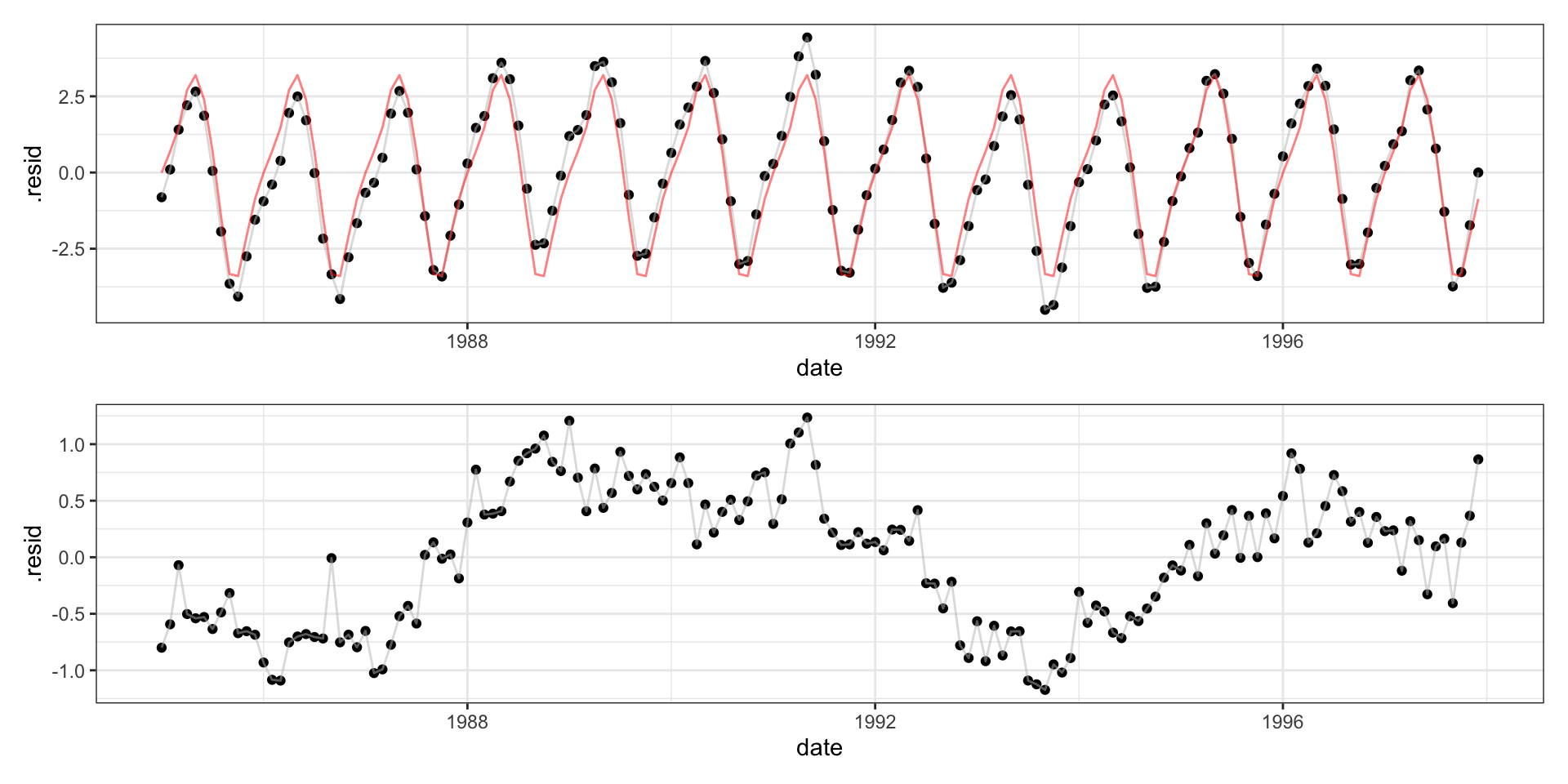
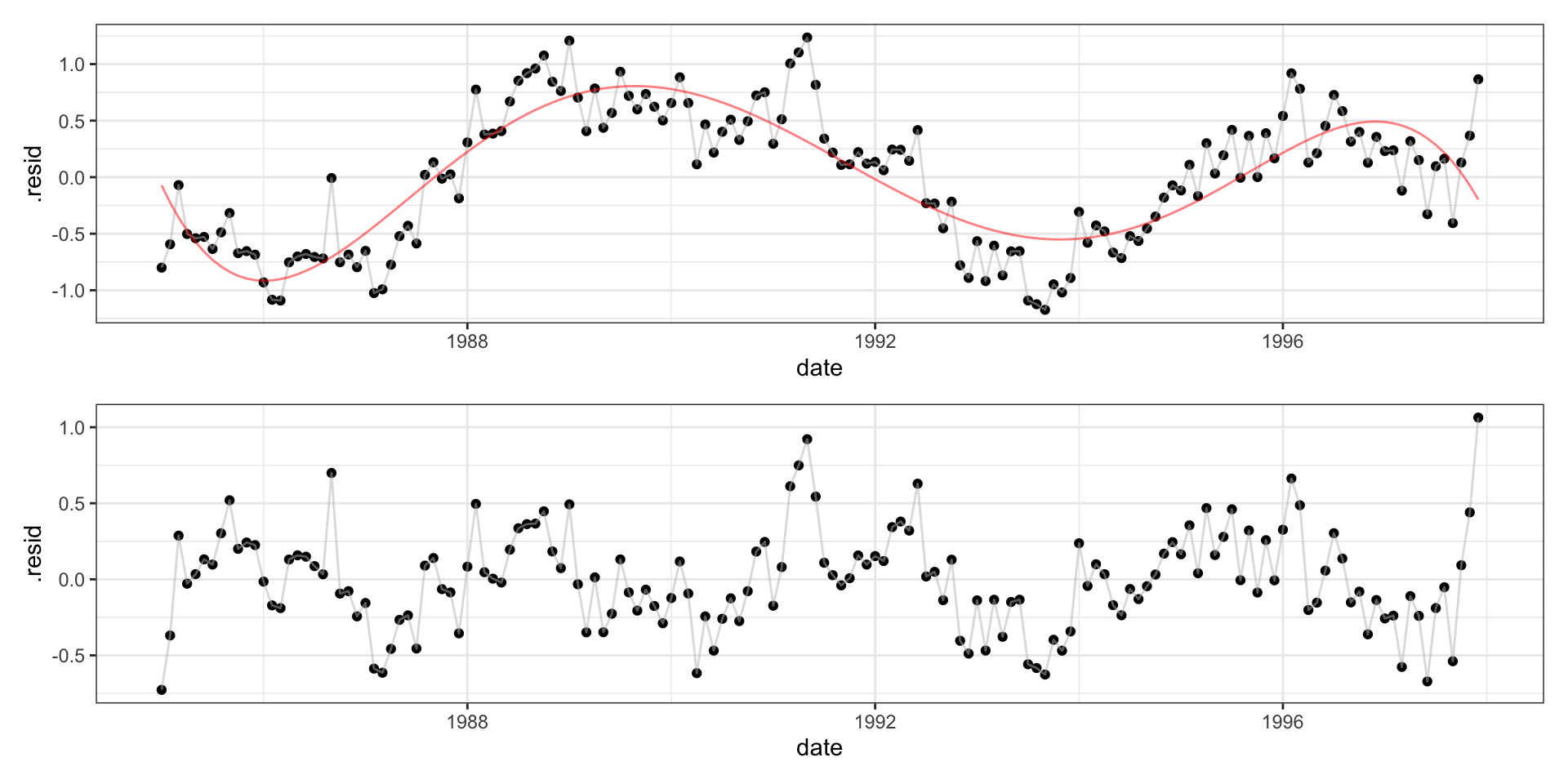
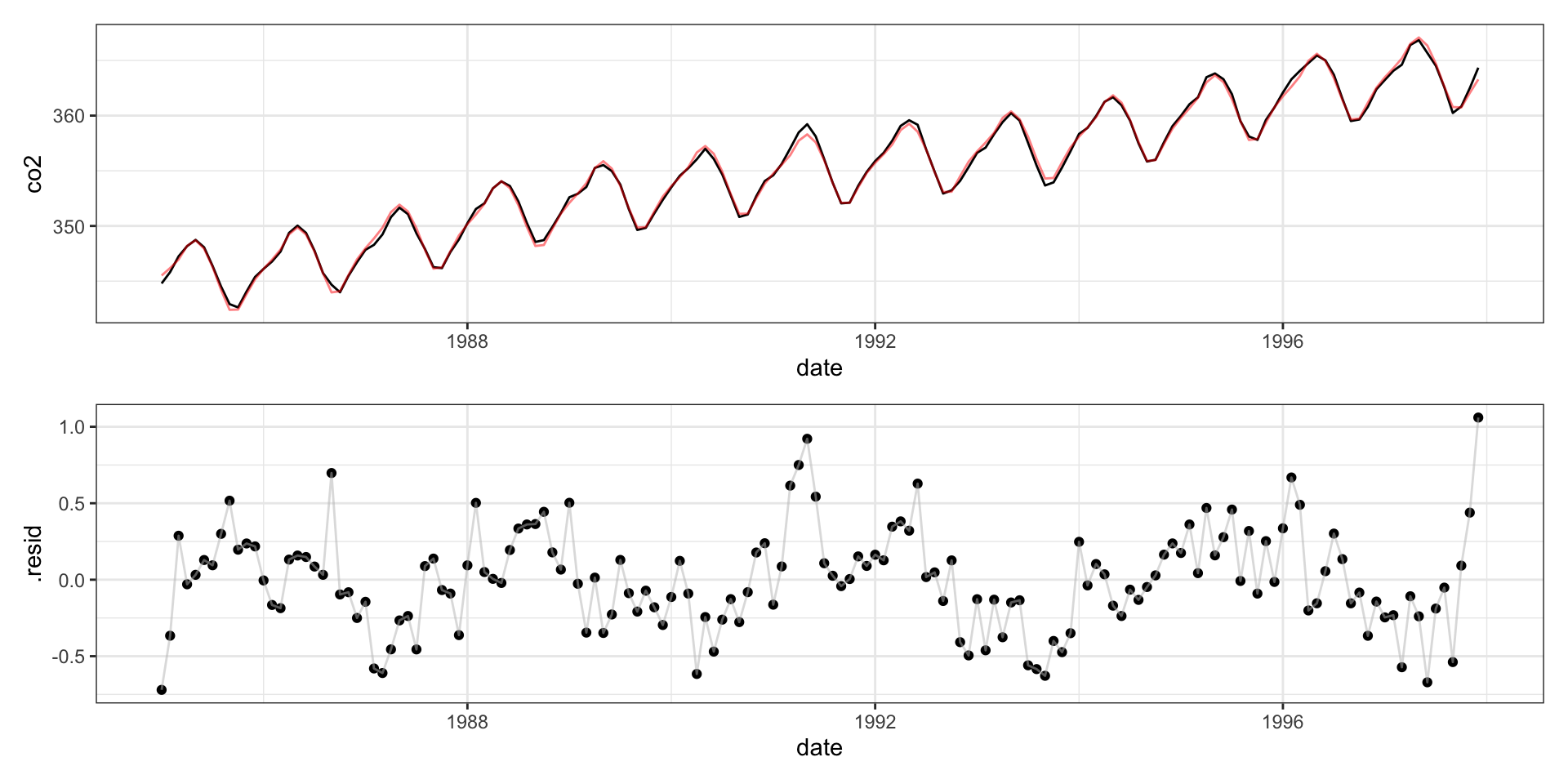
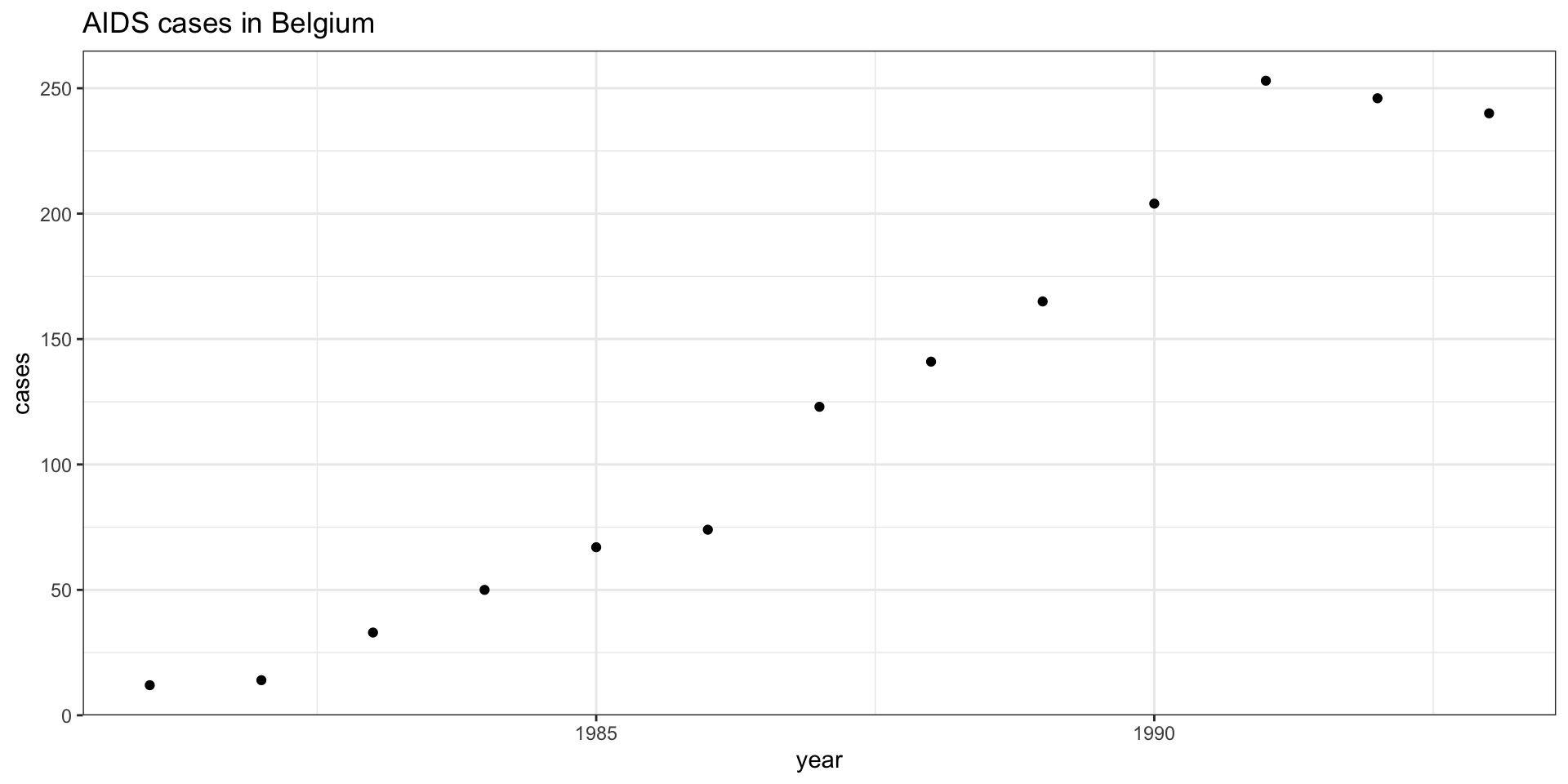
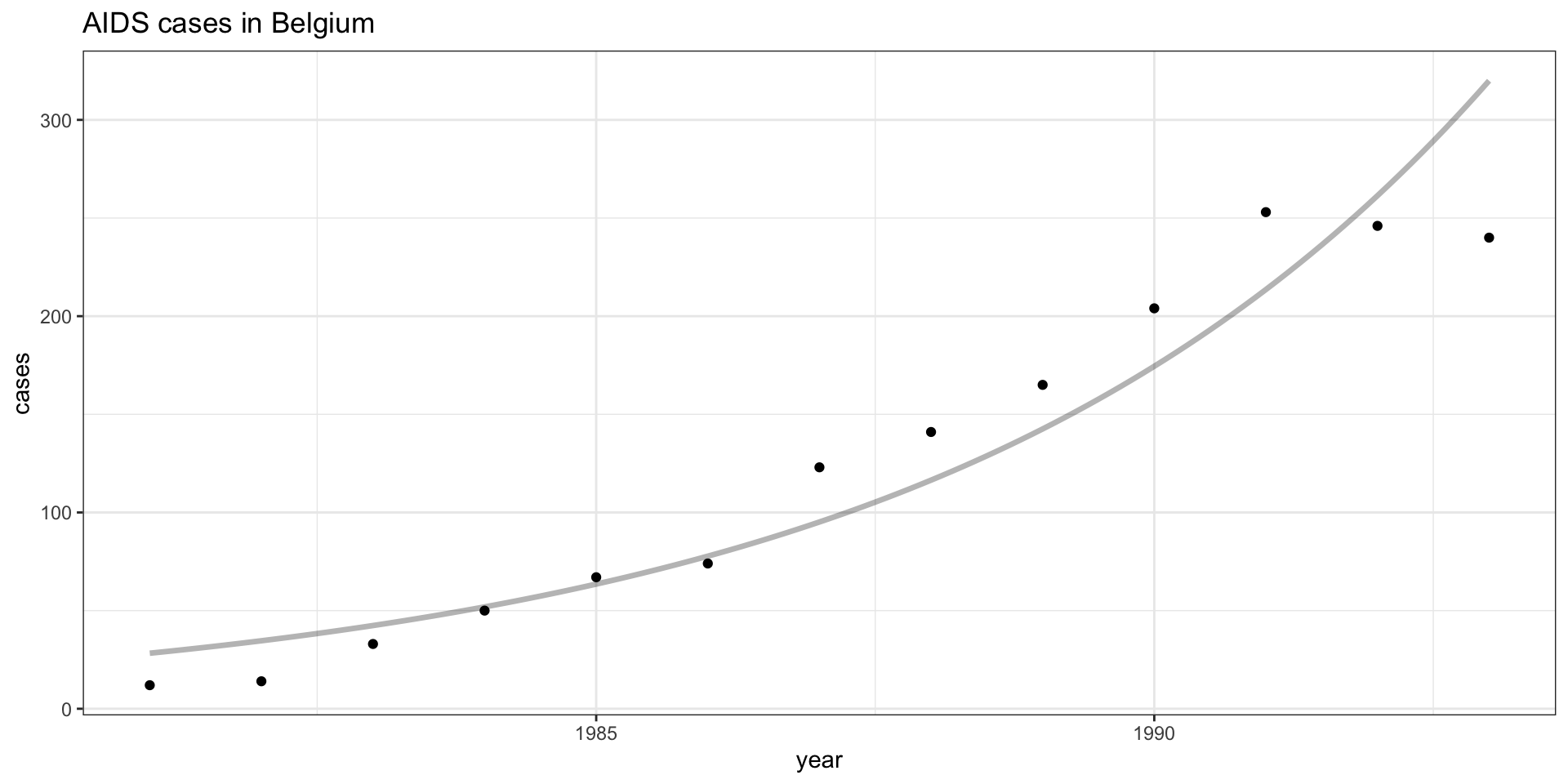
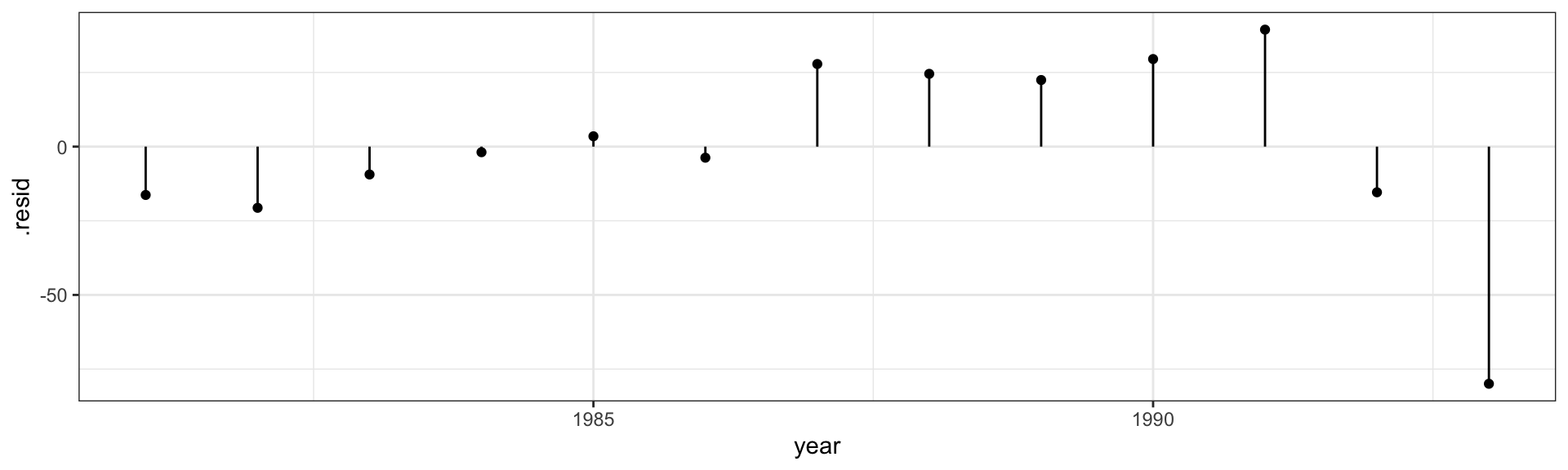
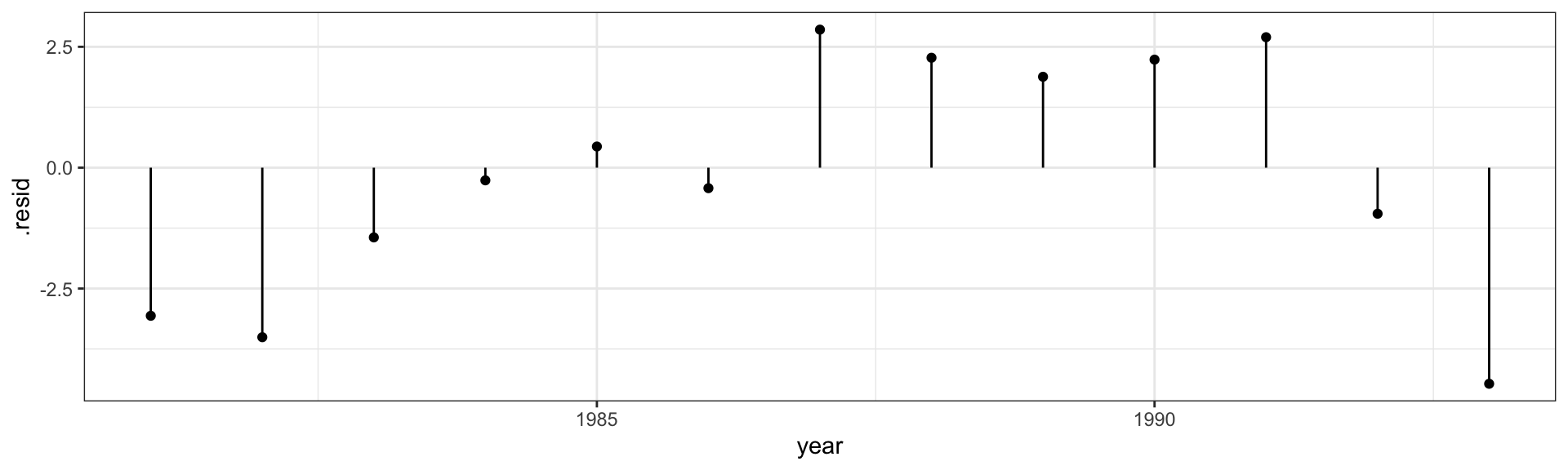
Call:
lm(formula = co2 ~ date + month + poly(date, 5), data = mauna_loa)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.72022 -0.19169 -0.00638  0.17565  1.06026 

Coefficients: (1 not defined because of singularities)
                 Estimate Std. Error  t value Pr(>|t|)    
(Intercept)    -2.587e+03  1.460e+01 -177.174  < 2e-16 ***
date            1.479e+00  7.334e-03  201.649  < 2e-16 ***
monthAug       -4.155e+00  1.346e-01  -30.880  < 2e-16 ***
monthDec       -3.566e+00  1.350e-01  -26.404  < 2e-16 ***
monthFeb       -2.022e+00  1.345e-01  -15.041  < 2e-16 ***
monthJan       -2.729e+00  1.345e-01  -20.286  < 2e-16 ***
monthJul       -2.018e+00  1.345e-01  -15.003  < 2e-16 ***
monthJun       -3.136e-01  1.345e-01   -2.332 0.021117 *  
monthMar       -1.233e+00  1.344e-01   -9.175 5.54e-16 ***
monthMay        4.881e-01  1.344e-01    3.631 0.000396 ***
monthNov       -4.799e+00  1.349e-01  -35.577  < 2e-16 ***
monthOct       -6.102e+00  1.348e-01  -45.282  < 2e-16 ***
monthSep       -6.036e+00  1.346e-01  -44.832  < 2e-16 ***
poly(date, 5)1         NA         NA       NA       NA    
poly(date, 5)2 -1.920e+00  3.427e-01   -5.602 1.09e-07 ***
poly(date, 5)3  3.920e+00  3.451e-01   11.358  < 2e-16 ***
poly(date, 5)4  8.946e-01  3.428e-01    2.609 0.010062 *  
poly(date, 5)5 -4.340e+00  3.462e-01  -12.535  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3427 on 139 degrees of freedom
Multiple R-squared:  0.997, Adjusted R-squared:  0.9966 
F-statistic:  2872 on 16 and 139 DF,  p-value: < 2.2e-16

Combined fit + Residuals

Model performance

Model	rmse
co2 ~ date	2.248
co2 ~ month	5.566
co2 ~ date+month	0.594
co2 ~ poly(date,5)	2.171
co2 ~ month+poly(date,5)	0.323
co2 ~ date+month+poly(date,5)	0.323

Generalized Linear Models

Background

A generalized linear model has three key components:

1. a probability distribution (from the exponential family) that describes your response variable

2. a linear predictor \(\boldsymbol{\eta} = \boldsymbol{X}\boldsymbol{\beta}\),

3. and a link function \(g\) such that \(g(E(\boldsymbol{Y}|\boldsymbol{X})) = \boldsymbol{\eta}\) (or \(E(\boldsymbol{Y}|\boldsymbol{X}) = g^{-1}(\boldsymbol{\eta})\)).

Poisson Regression

This is a special case of a generalized linear model for count data where we assume the outcome variable follows a poisson distribution (mean = variance).

\[ \begin{aligned} Y_i &\sim \text{Poisson}(\lambda_i)\\ \log E(Y_i|\boldsymbol{X}_{i\cdot}) &= \log{\lambda_i} = \underset{1 \times p}{\boldsymbol{X}_{i\cdot}}\underset{p \times 1}{\boldsymbol{\beta}} \end{aligned} \]

Example - AIDS in Belgium

These data represent the total number of new AIDS cases reported in Belgium during the early stages of the epidemic.

aids

# A tibble: 13 × 2
    year cases
   <int> <int>
 1  1981    12
 2  1982    14
 3  1983    33
 4  1984    50
 5  1985    67
 6  1986    74
 7  1987   123
 8  1988   141
 9  1989   165
10  1990   204
11  1991   253
12  1992   246
13  1993   240

Frequentist glm fit

( g = glm(cases~year, data=aids, family=poisson) )

Call:  glm(formula = cases ~ year, family = poisson, data = aids)

Coefficients:
(Intercept)         year  
  -397.0594       0.2021  

Degrees of Freedom: 12 Total (i.e. Null);  11 Residual
Null Deviance:      872.2 
Residual Deviance: 80.69    AIC: 166.4

Model Fit

g_pred = broom::augment(
  g, type.predict = "response", 
  newdata = tibble(year=seq(1981,1993,by=0.1))
)

aids_base + 
  geom_line(data=g_pred, aes(y=.fitted), size=1.2, alpha=0.3)

Residuals?

The naive approach is to use standard residuals,

\[ r_i = Y_i - E(Y_i|X) = Y_i - \hat\lambda_i\]

g_pred_std = broom::augment(
  g, type.predict = "response"
) %>%
  mutate(.resid = cases - .fitted)

Accounting for variability

Pearson residuals: \[ r_i = \frac{Y_i - E(Y_i|X)}{\sqrt{Var(Y_i|X)}} = \frac{Y_i - \hat\lambda_i}{\sqrt{\hat\lambda_i}}\]

g_pred_pearson = broom::augment(
  g, type.predict = "response", type.residuals = "pearson"
)

Deviance

Deviance is a way of measuring the difference between a GLM’s fit and the fit of the perfect model (i.e. where \(\theta_best = E(Y_i|X) = Y_i\)).

It is defined as twice the log of the ratio between the likelihood of the perfect model and the likelihood of the given model, \[ \begin{aligned} D &= 2\log\left( \frac{\mathcal{L}(\theta_{best}|Y)} { \mathcal{L}(\hat\theta|Y)}\right) \\ &= 2\big(\mathcal{l}(\theta_{best}|Y) - \mathcal{l}(\hat\theta|Y)\big) \end{aligned} \]

Derivation - Normal

Derivation - Poisson

glm output

summary(g)

Call:
glm(formula = cases ~ year, family = poisson, data = aids)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-4.6784  -1.5013  -0.2636   2.1760   2.7306  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.971e+02  1.546e+01  -25.68   <2e-16 ***
year         2.021e-01  7.771e-03   26.01   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 872.206  on 12  degrees of freedom
Residual deviance:  80.686  on 11  degrees of freedom
AIC: 166.37

Number of Fisher Scoring iterations: 4

Deviance residuals

We can therefore think of deviance as \(D = \sum_{i=1}^n d_i^2\) where \(d_i\) is a generalized residual.

In the Poisson case we have, \[ d_i = \text{sign}(y_i - \lambda_i) \sqrt{2(y_i \log (y_i/\hat\lambda_i) - (y_i-\hat\lambda_i))}\]

g_pred_dev = broom::augment(
  g, type.predict = "response", type.residuals = "deviance"
)

Comparing Residuals

Updating the model

Quadratic fit

g2 = glm(cases~year+I(year^2), data=aids, family=poisson)

g2_pred = broom::augment(
  g2, type.predict = "response",
  newdata=tibble(year=seq(1981,1993,by=0.1))
) 

Quadratic fit - residuals

Bayesian Model

Bayesian Poisson Regression Model

( g_bayes = brms::brm(
    cases~year, data=aids, family=poisson,
    silent=2, refresh=0
) )

 Family: poisson 
  Links: mu = log 
Formula: cases ~ year 
   Data: aids (Number of observations: 13) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept  -397.04     15.92  -428.85  -365.05 1.00     1381     1618
year          0.20      0.01     0.19     0.22 1.00     1382     1605

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Model priors

brms::prior_summary(g_bayes)

                  prior     class coef group resp dpar nlpar lb ub       source
                 (flat)         b                                       default
                 (flat)         b year                             (vectorized)
 student_t(3, 4.8, 2.5) Intercept                                       default

MCMC Diagnostics

plot(g_bayes)

Posterior Predictive Check

brms::pp_check(g_bayes)

Model fit - \(\lambda\) CI

aids_base +
  tidybayes::stat_lineribbon(
    data = tidybayes::epred_draws(
      g_bayes,
      newdata = tibble(year=seq(1981,1993,by=0.1))
    ),
    aes(y=.epred),
    alpha=0.25
  )

Model fit - \(Y\) CI

aids_base +
  tidybayes::stat_lineribbon(
    data = tidybayes::predicted_draws(
      g_bayes,
      newdata = tibble(year=seq(1981,1993,by=0.1))
    ),
    aes(y=.prediction),
    alpha=0.25
  )