Diagnostics and
Model Evaluation

Lecture 03

Dr. Colin Rundel

Some more linear models

Linear model and data

ggplot(d, aes(x=x,y=y)) + 
  geom_point() + 
  geom_smooth(method="lm", color="blue", se = FALSE)

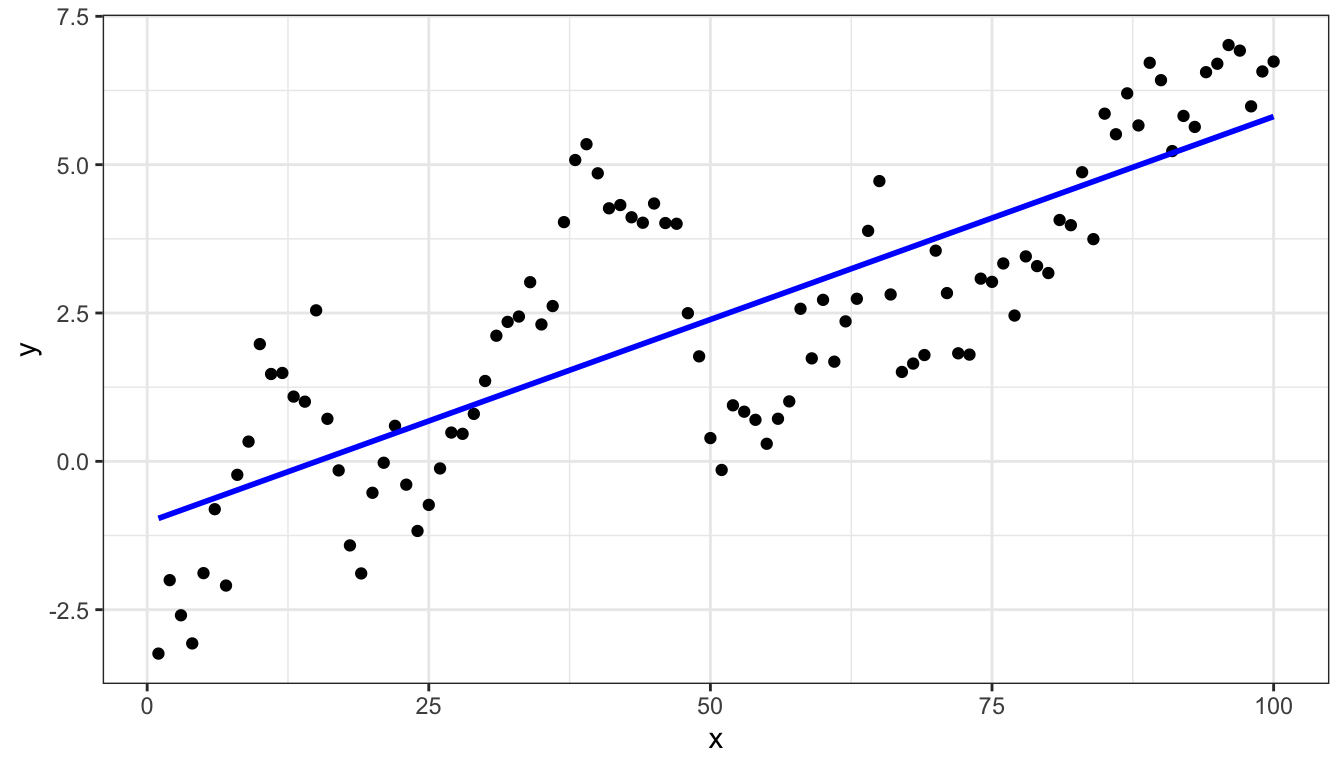
Linear model

l = lm(y ~ x, data=d)
summary(l)
## 
## Call:
## lm(formula = y ~ x, data = d)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.6041 -1.2142 -0.1973  1.1969  3.7072 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.030315   0.310326   -3.32  0.00126 ** 
## x            0.068409   0.005335   12.82  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.54 on 98 degrees of freedom
## Multiple R-squared:  0.6266, Adjusted R-squared:  0.6227 
## F-statistic: 164.4 on 1 and 98 DF,  p-value: < 2.2e-16

Bayesian model (brms)

( b = brms::brm(
    y ~ x, data=d,
    prior = c(
      brms::prior(normal(0, 100), class = Intercept),
      brms::prior(normal(0, 10),  class = b),
      brms::prior(cauchy(0, 2),   class = sigma)
    ),
    silent = 2, refresh = 0
  )
)
## Running /opt/homebrew/Cellar/r/4.2.1_2/lib/R/bin/R CMD SHLIB foo.c
## clang -I"/opt/homebrew/Cellar/r/4.2.1_2/lib/R/include" -DNDEBUG   -I"/Users/rundel/Library/R/arm64/4.2/library/Rcpp/include/"  -I"/Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/"  -I"/Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/unsupported"  -I"/Users/rundel/Library/R/arm64/4.2/library/BH/include" -I"/Users/rundel/Library/R/arm64/4.2/library/StanHeaders/include/src/"  -I"/Users/rundel/Library/R/arm64/4.2/library/StanHeaders/include/"  -I"/Users/rundel/Library/R/arm64/4.2/library/RcppParallel/include/"  -I"/Users/rundel/Library/R/arm64/4.2/library/rstan/include" -DEIGEN_NO_DEBUG  -DBOOST_DISABLE_ASSERTS  -DBOOST_PENDING_INTEGER_LOG2_HPP  -DSTAN_THREADS  -DBOOST_NO_AUTO_PTR  -include '/Users/rundel/Library/R/arm64/4.2/library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp'  -D_REENTRANT -DRCPP_PARALLEL_USE_TBB=1   -I/opt/homebrew/opt/gettext/include -I/opt/homebrew/opt/readline/include -I/opt/homebrew/opt/xz/include -I/opt/homebrew/include   -fPIC  -Wno-implicit-function-declaration  -c foo.c -o foo.o
## In file included from <built-in>:1:
## In file included from /Users/rundel/Library/R/arm64/4.2/library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:13:
## In file included from /Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/Eigen/Dense:1:
## In file included from /Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/Eigen/Core:88:
## /Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:1: error: unknown type name 'namespace'
## namespace Eigen {
## ^
## /Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:628:16: error: expected ';' after top level declarator
## namespace Eigen {
##                ^
##                ;
## In file included from <built-in>:1:
## In file included from /Users/rundel/Library/R/arm64/4.2/library/StanHeaders/include/stan/math/prim/mat/fun/Eigen.hpp:13:
## In file included from /Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/Eigen/Dense:1:
## /Users/rundel/Library/R/arm64/4.2/library/RcppEigen/include/Eigen/Core:96:10: fatal error: 'complex' file not found
## #include <complex>
##          ^~~~~~~~~
## 3 errors generated.
## make: *** [foo.o] Error 1
##  Family: gaussian 
##   Links: mu = identity; sigma = identity 
## Formula: y ~ x 
##    Data: d (Number of observations: 100) 
##   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
##          total post-warmup draws = 4000
## 
## Population-Level Effects: 
##           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept    -1.03      0.31    -1.63    -0.43 1.00     4431     2639
## x             0.07      0.01     0.06     0.08 1.00     5244     2691
## 
## Family Specific Parameters: 
##       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma     1.55      0.11     1.36     1.78 1.00     3287     2616
## 
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).

Parameter estimates

plot(b)

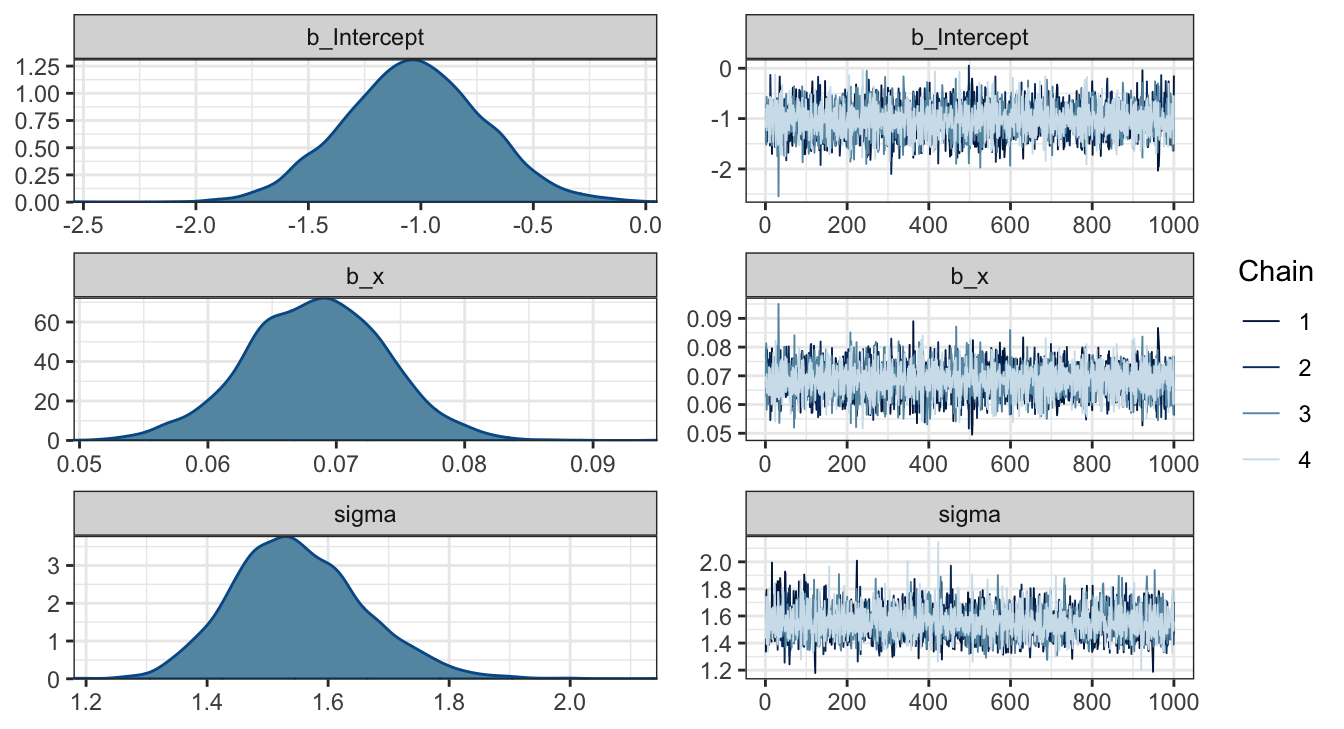
tidybayes - gather_draws (long)

b_post = b |>
  tidybayes::gather_draws(b_Intercept, b_x, sigma)

b_post
## # A tibble: 12,000 × 5
## # Groups:   .variable [3]
##    .chain .iteration .draw .variable   .value
##     <int>      <int> <int> <chr>        <dbl>
##  1      1          1     1 b_Intercept -0.961
##  2      1          2     2 b_Intercept -1.24 
##  3      1          3     3 b_Intercept -1.29 
##  4      1          4     4 b_Intercept -0.763
##  5      1          5     5 b_Intercept -0.980
##  6      1          6     6 b_Intercept -1.13 
##  7      1          7     7 b_Intercept -0.810
##  8      1          8     8 b_Intercept -1.33 
##  9      1          9     9 b_Intercept -1.22 
## 10      1         10    10 b_Intercept -1.11 
## # … with 11,990 more rows

tidybayes - spread_draws (wide)

b_post_wide = b |>
  tidybayes::spread_draws(b_Intercept, b_x, sigma)

b_post_wide
## # A tibble: 4,000 × 6
##    .chain .iteration .draw b_Intercept    b_x sigma
##     <int>      <int> <int>       <dbl>  <dbl> <dbl>
##  1      1          1     1      -0.961 0.0671  1.33
##  2      1          2     2      -1.24  0.0726  1.75
##  3      1          3     3      -1.29  0.0736  1.79
##  4      1          4     4      -0.763 0.0639  1.35
##  5      1          5     5      -0.980 0.0697  1.53
##  6      1          6     6      -1.13  0.0692  1.53
##  7      1          7     7      -0.810 0.0637  1.52
##  8      1          8     8      -1.33  0.0726  1.47
##  9      1          9     9      -1.22  0.0728  1.65
## 10      1         10    10      -1.11  0.0667  1.52
## # … with 3,990 more rows

Posterior plots

b_post |>
  ggplot(aes(fill=as.factor(.chain), group=.chain, x=.value)) +
  geom_density(alpha=0.33, color=NA) +
  facet_wrap(~.variable, scales = "free")

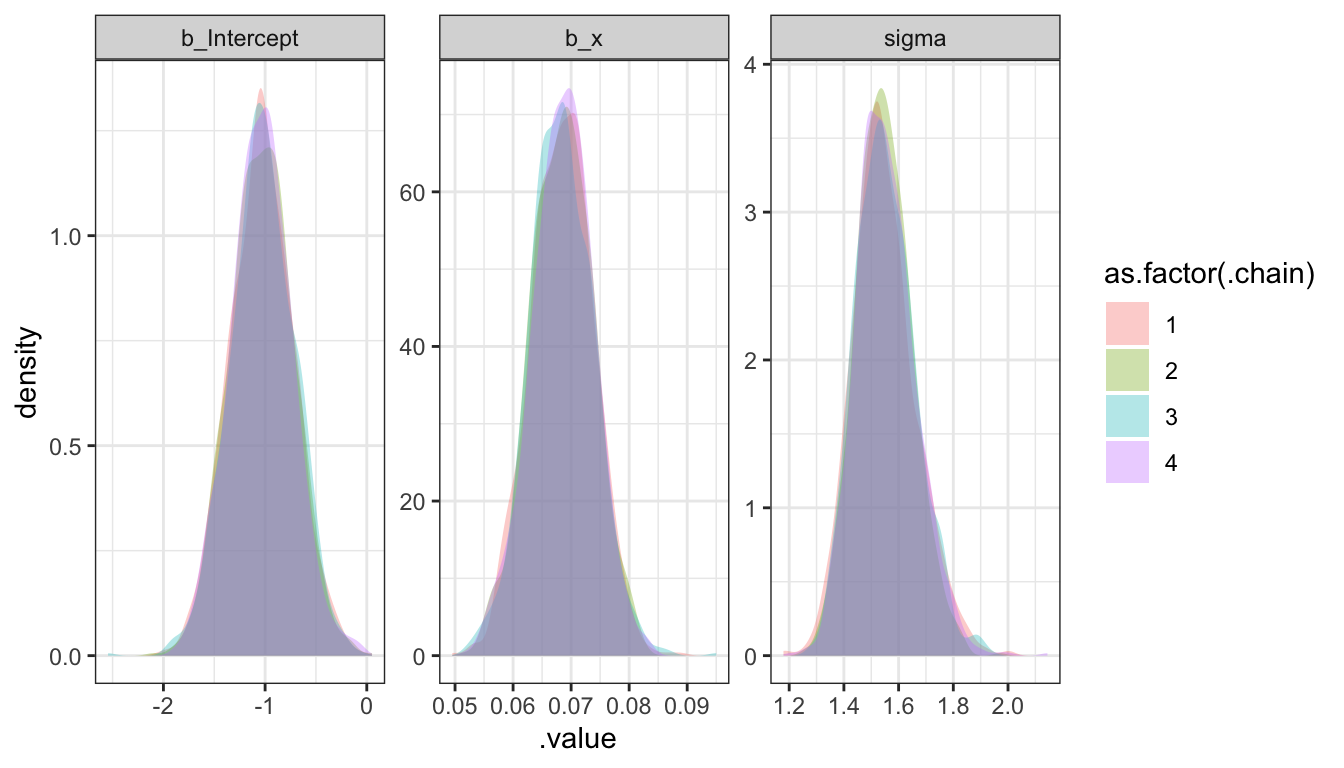
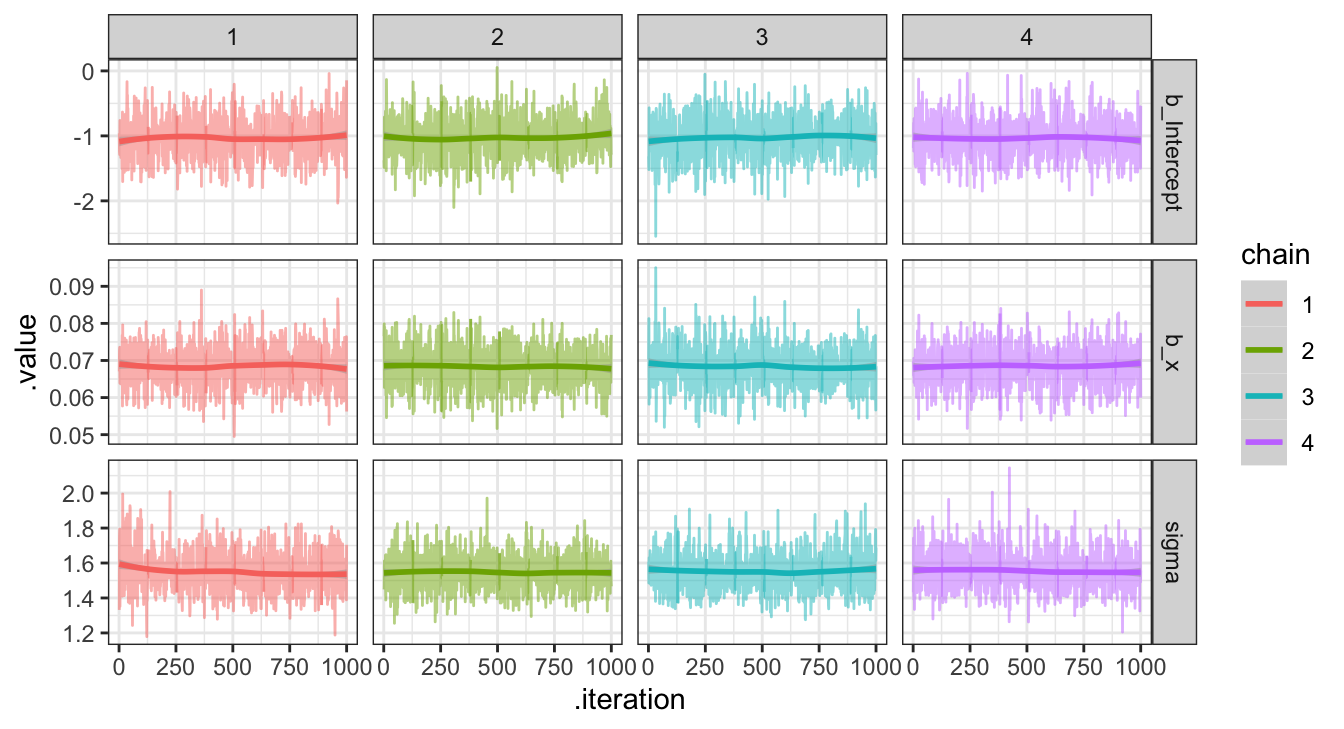
Trace plots

b_post %>% 
  ggplot(aes(x=.iteration, y=.value, color=as.factor(.chain))) +
  geom_line(alpha=0.5) +
  facet_grid(.variable~.chain, scale="free_y") +
  geom_smooth(method="loess") + labs(color="chain")

Credible Intervals

( b_ci = b_post |>
    group_by(.chain, .variable) |>
    tidybayes::mean_hdi(.value, .width=c(0.8, 0.95))
)
## # A tibble: 24 × 8
##    .chain .variable    .value  .lower  .upper .width .point .interval
##     <int> <chr>         <dbl>   <dbl>   <dbl>  <dbl> <chr>  <chr>    
##  1      1 b_Intercept -1.03   -1.40   -0.624     0.8 mean   hdi      
##  2      1 b_x          0.0685  0.0624  0.0761    0.8 mean   hdi      
##  3      1 sigma        1.55    1.40    1.69      0.8 mean   hdi      
##  4      2 b_Intercept -1.03   -1.41   -0.621     0.8 mean   hdi      
##  5      2 b_x          0.0684  0.0620  0.0753    0.8 mean   hdi      
##  6      2 sigma        1.55    1.43    1.69      0.8 mean   hdi      
##  7      3 b_Intercept -1.02   -1.40   -0.604     0.8 mean   hdi      
##  8      3 b_x          0.0684  0.0615  0.0749    0.8 mean   hdi      
##  9      3 sigma        1.55    1.42    1.69      0.8 mean   hdi      
## 10      4 b_Intercept -1.04   -1.40   -0.637     0.8 mean   hdi      
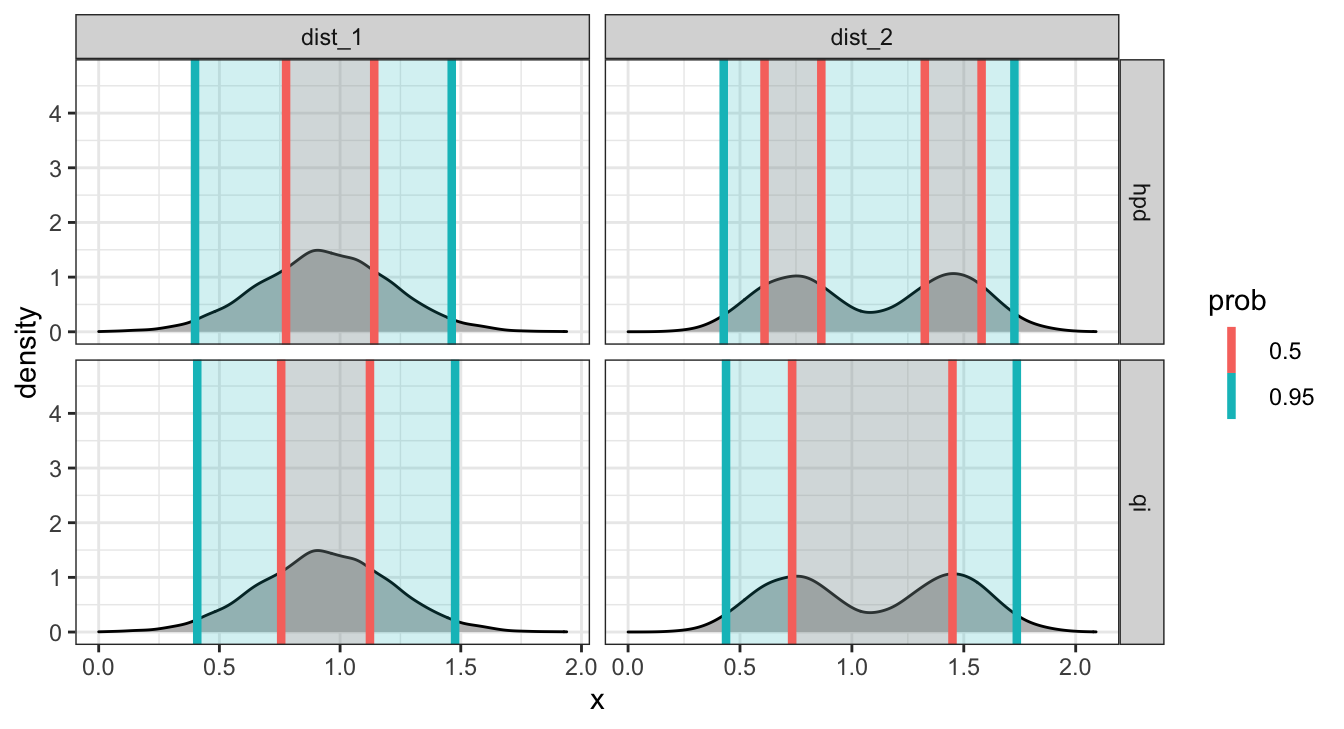
## # … with 14 more rows

Aside - mean_qi() vs mean_hdi()

These differ in the use of the quantile interval vs. the highest-density interval.

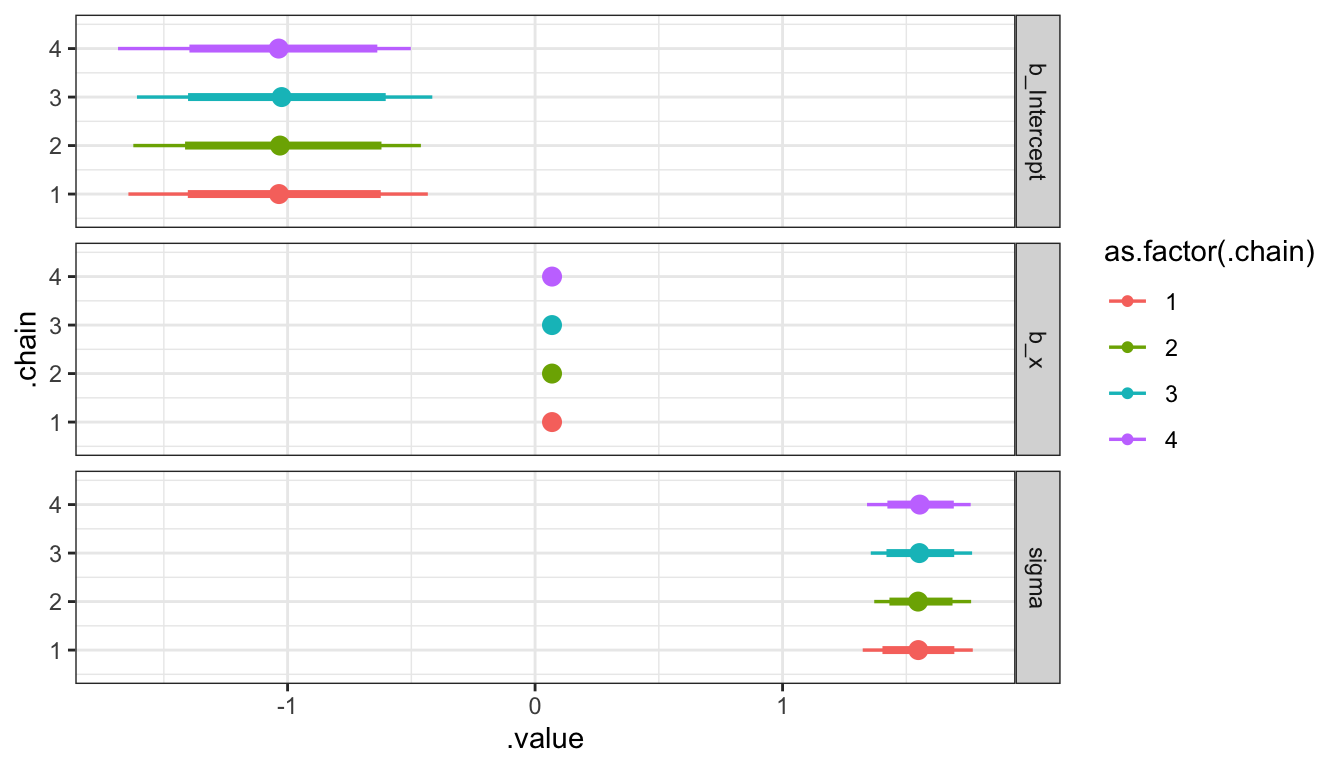
Caterpillar Plots

b_ci %>%
  ggplot(aes(x=.value, y=.chain, color=as.factor(.chain))) + 
  facet_grid(.variable ~ .) +
  tidybayes::geom_pointintervalh() +
  ylim(0.5, 4.5)

Predictions

lm predictions

(l_pred = broom::augment(l, interval="confidence"))
## # A tibble: 100 × 10
##         y     x .fitted .lower   .upper .resid   .hat .sigma  .cooksd .std.resid
##     <dbl> <int>   <dbl>  <dbl>    <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
##  1 -3.24      1  -0.962 -1.57  -0.355   -2.28  0.0394   1.53 0.0467       -1.51 
##  2 -2.00      2  -0.893 -1.49  -0.296   -1.11  0.0382   1.54 0.0107       -0.734
##  3 -2.59      3  -0.825 -1.41  -0.237   -1.77  0.0371   1.54 0.0264       -1.17 
##  4 -3.07      4  -0.757 -1.34  -0.177   -2.31  0.0359   1.53 0.0436       -1.53 
##  5 -1.88      5  -0.688 -1.26  -0.118   -1.20  0.0348   1.54 0.0113       -0.791
##  6 -0.807     6  -0.620 -1.18  -0.0583  -0.187 0.0338   1.55 0.000266     -0.123
##  7 -2.09      7  -0.551 -1.10   0.00127 -1.54  0.0327   1.54 0.0175       -1.02 
##  8 -0.227     8  -0.483 -1.03   0.0609   0.256 0.0317   1.55 0.000466      0.169
##  9  0.333     9  -0.415 -0.950  0.121    0.747 0.0307   1.55 0.00384       0.493
## 10  1.98     10  -0.346 -0.873  0.180    2.32  0.0297   1.53 0.0358        1.53 
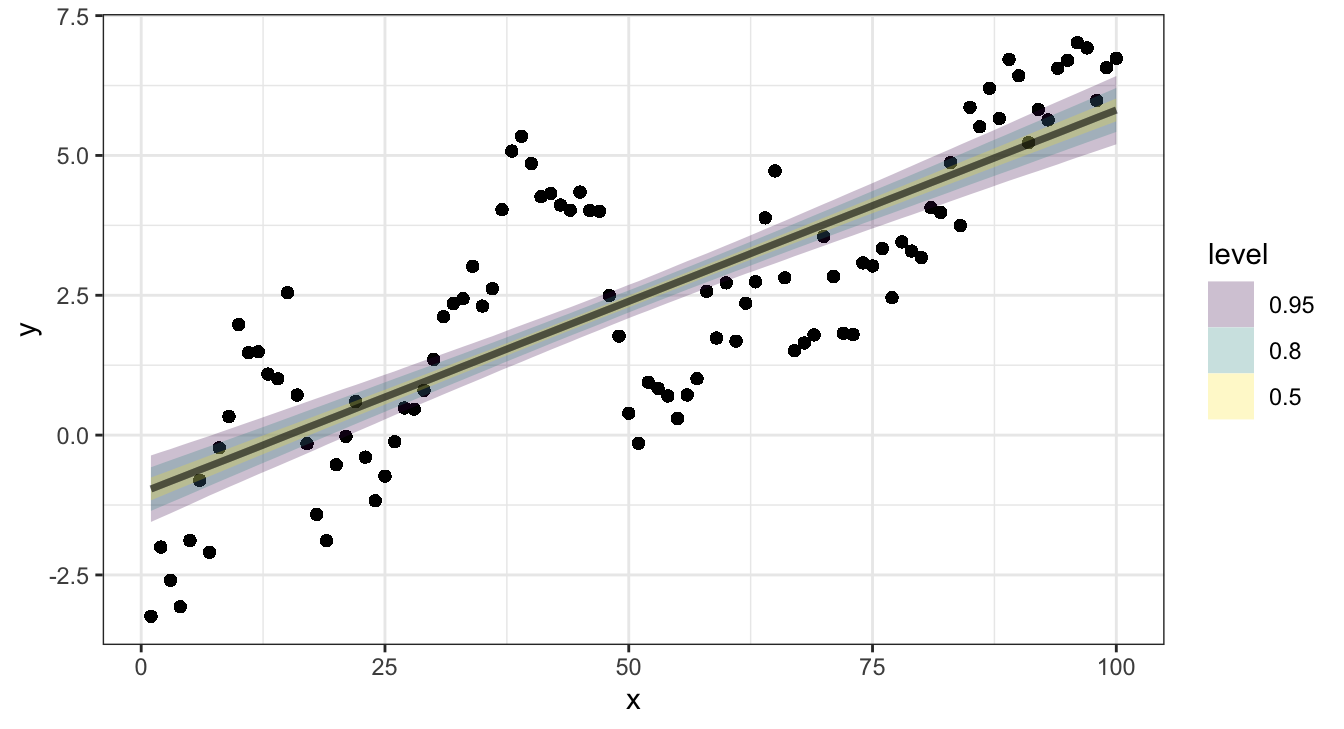
## # … with 90 more rows

There are the same values you would get from predict(l, se.fit = TRUE) just combined with d

Confidence interval

l_pred |>
  ggplot(aes(x=x,y=y)) + 
   geom_point() +
   geom_line(aes(y=.fitted), col="blue", size=1.5) +
   geom_ribbon(aes(ymin=.lower, ymax=.upper), col="blue", fill="blue", alpha=0.33)

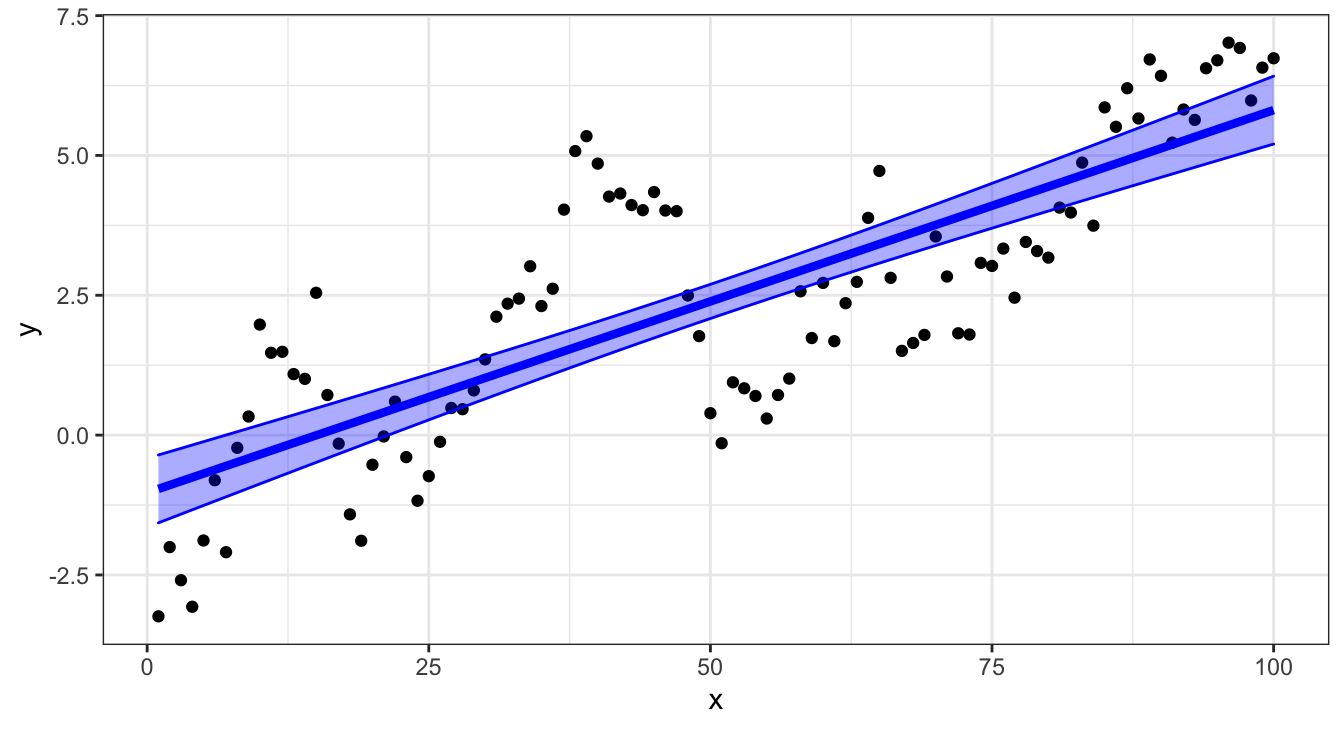
brms predictions

(b_pred = predict(b))
##           Estimate Est.Error        Q2.5    Q97.5
##   [1,] -0.96419044  1.553634 -4.04028547 2.124732
##   [2,] -0.89721849  1.593799 -3.96603496 2.179769
##   [3,] -0.79179315  1.594565 -3.96413800 2.391643
##   [4,] -0.73859326  1.579550 -3.83546564 2.266440
##   [5,] -0.68293418  1.579669 -3.79089154 2.460559
##   [6,] -0.61155250  1.609090 -3.81348198 2.516711
##   [7,] -0.56675460  1.579506 -3.66369377 2.479165
##   [8,] -0.45334581  1.570071 -3.47909432 2.620280
##   [9,] -0.47151098  1.565524 -3.49855796 2.580172
##  [10,] -0.35537333  1.552547 -3.30957100 2.739897
##  [11,] -0.26908970  1.562577 -3.30266874 2.745822
##  [12,] -0.20382232  1.582830 -3.19318502 2.973233
##  [13,] -0.18236463  1.568774 -3.25612849 3.056613
##  [14,] -0.03840721  1.571181 -3.10470573 3.032293
##  [15,] -0.00652744  1.572307 -3.12245894 3.008274
##  [16,]  0.10287639  1.572319 -3.00472461 3.249254
##  [17,]  0.13118291  1.551076 -2.95438203 3.215593
##  [18,]  0.17851264  1.584728 -2.98651983 3.299391
##  [19,]  0.27050750  1.563454 -2.87319847 3.363364
##  [20,]  0.41283775  1.573038 -2.66079563 3.530289
##  [21,]  0.44184881  1.555286 -2.56097614 3.577824
##  [22,]  0.49217845  1.563060 -2.59018856 3.618380
##  [23,]  0.55265549  1.569987 -2.55004713 3.696949
##  [24,]  0.58250043  1.566227 -2.46261938 3.659840
##  [25,]  0.68590865  1.572495 -2.40520333 3.683899
##  [26,]  0.72963017  1.543954 -2.23608029 3.789787
##  [27,]  0.81039564  1.558351 -2.20547662 3.841632
##  [28,]  0.88280296  1.553211 -2.21481596 3.889175
##  [29,]  0.96859814  1.545373 -2.01290488 3.995431
##  [30,]  1.03721604  1.553376 -2.09335175 4.076215
##  [31,]  1.08407921  1.547029 -1.87896160 4.168488
##  [32,]  1.17290777  1.565596 -1.83976815 4.310560
##  [33,]  1.26850017  1.565206 -1.73367094 4.384727
##  [34,]  1.28279024  1.560946 -1.75673259 4.393507
##  [35,]  1.38357784  1.540426 -1.59904748 4.397953
##  [36,]  1.44710794  1.578714 -1.71632818 4.442580
##  [37,]  1.53174657  1.569852 -1.58157999 4.546611
##  [38,]  1.56547981  1.558802 -1.48783191 4.584533
##  [39,]  1.62184547  1.607951 -1.57322312 4.750295
##  [40,]  1.67600652  1.563986 -1.43433051 4.706720
##  [41,]  1.77823618  1.565591 -1.32955716 4.852990
##  [42,]  1.87565665  1.543720 -1.11319802 4.864384
##  [43,]  1.92136023  1.536899 -1.07187048 5.065492
##  [44,]  1.99608460  1.547342 -0.99295043 5.116418
##  [45,]  2.03431203  1.527837 -0.92298442 5.079693
##  [46,]  2.17601221  1.540681 -0.75118929 5.292158
##  [47,]  2.22583634  1.578335 -0.92872466 5.402889
##  [48,]  2.27637390  1.537809 -0.78925532 5.400552
##  [49,]  2.36065179  1.590575 -0.80086408 5.518619
##  [50,]  2.39429735  1.569579 -0.68372725 5.444640
##  [51,]  2.47232834  1.586458 -0.68805088 5.552497
##  [52,]  2.52157332  1.598191 -0.69885170 5.669854
##  [53,]  2.62977657  1.563467 -0.38517877 5.644701
##  [54,]  2.67094685  1.568177 -0.40028556 5.694188
##  [55,]  2.73663758  1.564255 -0.35934672 5.859088
##  [56,]  2.80989166  1.557385 -0.28249546 5.906563
##  [57,]  2.91005675  1.583946 -0.18362586 5.972365
##  [58,]  2.95733547  1.555786 -0.06794048 6.019356
##  [59,]  2.99627646  1.572688 -0.17323347 6.095180
##  [60,]  3.07966257  1.589372 -0.00439586 6.242303
##  [61,]  3.12656037  1.600794  0.06930962 6.345764
##  [62,]  3.18498011  1.554808  0.16128793 6.206373
##  [63,]  3.27165021  1.550771  0.18797397 6.298690
##  [64,]  3.32927738  1.572493  0.28464113 6.545312
##  [65,]  3.39355294  1.582995  0.31559142 6.443889
##  [66,]  3.45409957  1.532763  0.43493476 6.405158
##  [67,]  3.52064847  1.573354  0.38997121 6.555478
##  [68,]  3.62602785  1.588982  0.58327197 6.697734
##  [69,]  3.69378150  1.613452  0.47427503 6.802541
##  [70,]  3.73362593  1.571077  0.66092402 6.755425
##  [71,]  3.84334287  1.588937  0.79286368 6.964876
##  [72,]  3.93962741  1.560438  0.87969769 6.977364
##  [73,]  3.94629114  1.567417  0.83751669 7.068538
##  [74,]  4.02382853  1.576824  0.94269246 7.183349
##  [75,]  4.14212124  1.572508  1.08811598 7.218009
##  [76,]  4.14183389  1.546520  1.15590239 7.226831
##  [77,]  4.22485737  1.559249  1.22303133 7.255037
##  [78,]  4.30730427  1.576806  1.22050671 7.408303
##  [79,]  4.34446826  1.528154  1.37028014 7.454586
##  [80,]  4.43593391  1.581751  1.38209803 7.572422
##  [81,]  4.49717279  1.579947  1.42682090 7.619767
##  [82,]  4.57308158  1.557224  1.41422283 7.609957
##  [83,]  4.66299731  1.586878  1.51600868 7.662505
##  [84,]  4.68078297  1.571286  1.56934250 7.789015
##  [85,]  4.76934980  1.603489  1.63894211 7.877330
##  [86,]  4.84961212  1.578855  1.84134540 7.945473
##  [87,]  4.94564757  1.541860  1.96273553 8.019691
##  [88,]  4.99167332  1.572537  1.92861675 8.033702
##  [89,]  5.02422454  1.596433  1.91953291 8.079916
##  [90,]  5.14588414  1.606303  1.95928451 8.304882
##  [91,]  5.16011533  1.566905  2.07553352 8.230494
##  [92,]  5.27612394  1.590560  2.14222744 8.438877
##  [93,]  5.33182633  1.576197  2.28943018 8.460920
##  [94,]  5.42198182  1.620632  2.28758680 8.652370
##  [95,]  5.47389922  1.589344  2.33761040 8.593094
##  [96,]  5.54751511  1.594631  2.39575175 8.728021
##  [97,]  5.62311878  1.575677  2.54298645 8.683638
##  [98,]  5.63624251  1.599526  2.53240302 8.687367
##  [99,]  5.72299151  1.586211  2.56923647 8.886604
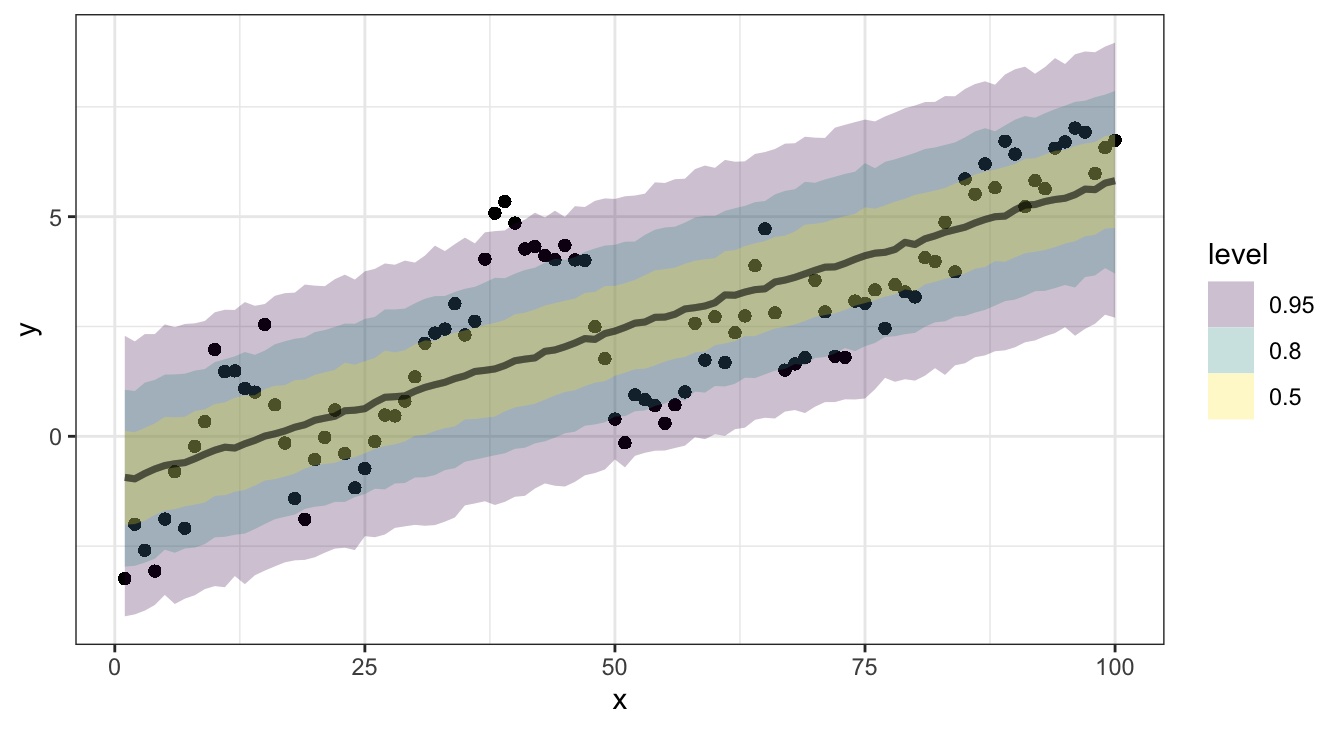
## [100,]  5.83129479  1.570594  2.78270719 8.901418

Credible interval

d |>
  bind_cols(b_pred) |>
  ggplot(aes(x=x,y=y)) + 
    geom_point() +
    geom_line(aes(y=Estimate), col="red", size=1.5) +
    geom_ribbon(aes(ymin=Q2.5, ymax=Q97.5), col='red', fill='red', alpha=0.33)

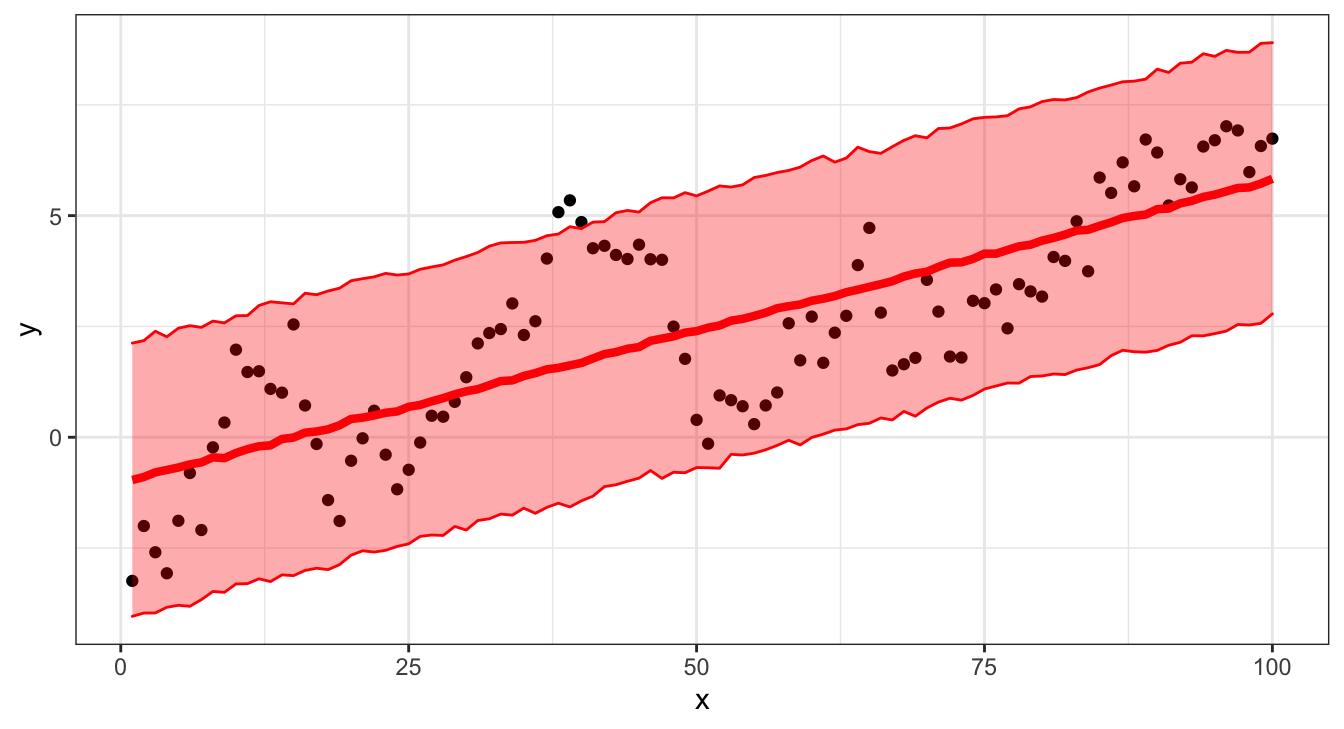
Why are the intervals different?

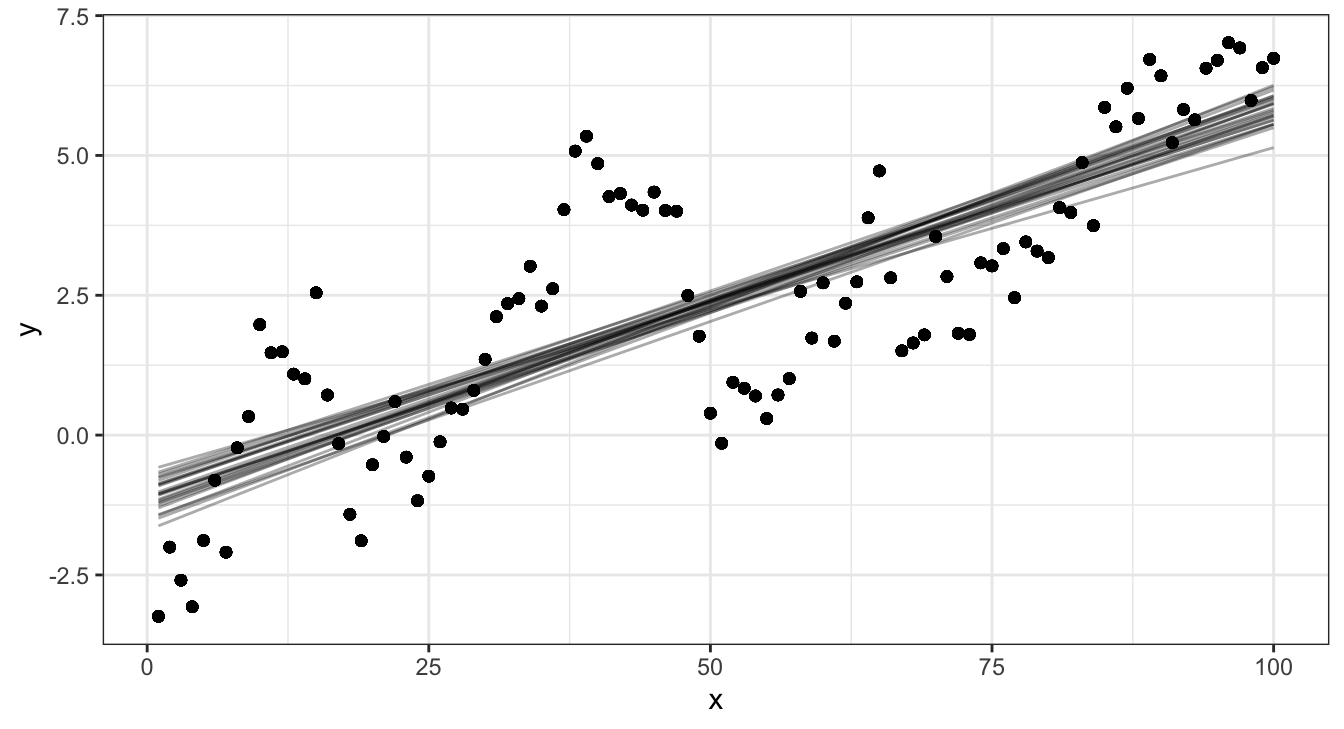
Raw predictions

dim( brms::posterior_predict(b) )
## [1] 4000  100
dim( brms::posterior_epred(b) )
## [1] 4000  100

Tidy raw predictions

( b_post_pred = tidybayes::predicted_draws(
    b, newdata=d
) )
## # A tibble: 400,000 × 7
## # Groups:   x, y, .row [100]
##        x     y  .row .chain .iteration .draw .prediction
##    <int> <dbl> <int>  <int>      <int> <int>       <dbl>
##  1     1 -3.24     1     NA         NA     1       3.24 
##  2     1 -3.24     1     NA         NA     2      -3.86 
##  3     1 -3.24     1     NA         NA     3      -1.36 
##  4     1 -3.24     1     NA         NA     4       0.465
##  5     1 -3.24     1     NA         NA     5      -2.54 
##  6     1 -3.24     1     NA         NA     6      -6.98 
##  7     1 -3.24     1     NA         NA     7      -2.07 
##  8     1 -3.24     1     NA         NA     8      -2.97 
##  9     1 -3.24     1     NA         NA     9      -0.408
## 10     1 -3.24     1     NA         NA    10      -0.465
## # … with 399,990 more rows

( b_post_epred = tidybayes::epred_draws(
    b, newdata=d
) )
## # A tibble: 400,000 × 7
## # Groups:   x, y, .row [100]
##        x     y  .row .chain .iteration .draw .epred
##    <int> <dbl> <int>  <int>      <int> <int>  <dbl>
##  1     1 -3.24     1     NA         NA     1 -0.894
##  2     1 -3.24     1     NA         NA     2 -1.17 
##  3     1 -3.24     1     NA         NA     3 -1.21 
##  4     1 -3.24     1     NA         NA     4 -0.699
##  5     1 -3.24     1     NA         NA     5 -0.910
##  6     1 -3.24     1     NA         NA     6 -1.06 
##  7     1 -3.24     1     NA         NA     7 -0.746
##  8     1 -3.24     1     NA         NA     8 -1.26 
##  9     1 -3.24     1     NA         NA     9 -1.15 
## 10     1 -3.24     1     NA         NA    10 -1.05 
## # … with 399,990 more rows

Posterior predictions vs Expected posterior predictions

b_post_pred |>
  filter(.draw <= 25) |>
  ggplot(aes(x=x,y=y)) +
    geom_point() +
    geom_line(
      aes(y=.prediction, group=.draw), 
      alpha=0.33
    )

b_post_epred |>
  filter(.draw <= 25) |>
  ggplot(aes(x=x,y=y)) +
    geom_point() +
    geom_line(
      aes(y=.epred, group=.draw), 
      alpha=0.33
    )

Credible intervals

b_post_pred |>
  ggplot(aes(x=x, y=y)) +
    geom_point() +
    tidybayes::stat_lineribbon(
      aes(y=.prediction), alpha=0.25
    )

b_post_epred |>
  ggplot(aes(x=x, y=y)) +
    geom_point() +
    tidybayes::stat_lineribbon(
      aes(y=.epred), alpha=0.25
    )

Posterior predictive checks

brms::pp_check(b, ndraws = 25)

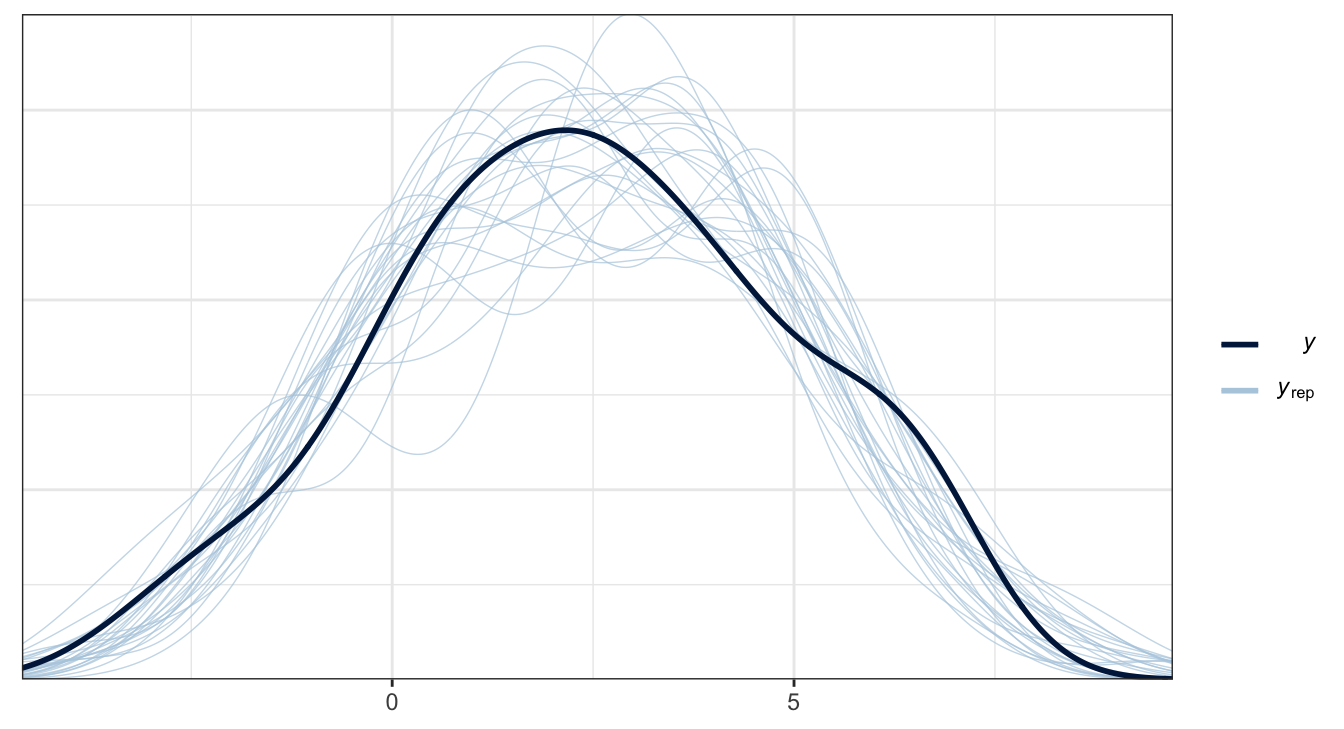
Residuals - lm

l |>
  broom::augment() |>
  ggplot(aes(x=x, y=.resid)) +
    geom_point() +
    geom_hline(yintercept=0, color='grey', linetype=2)

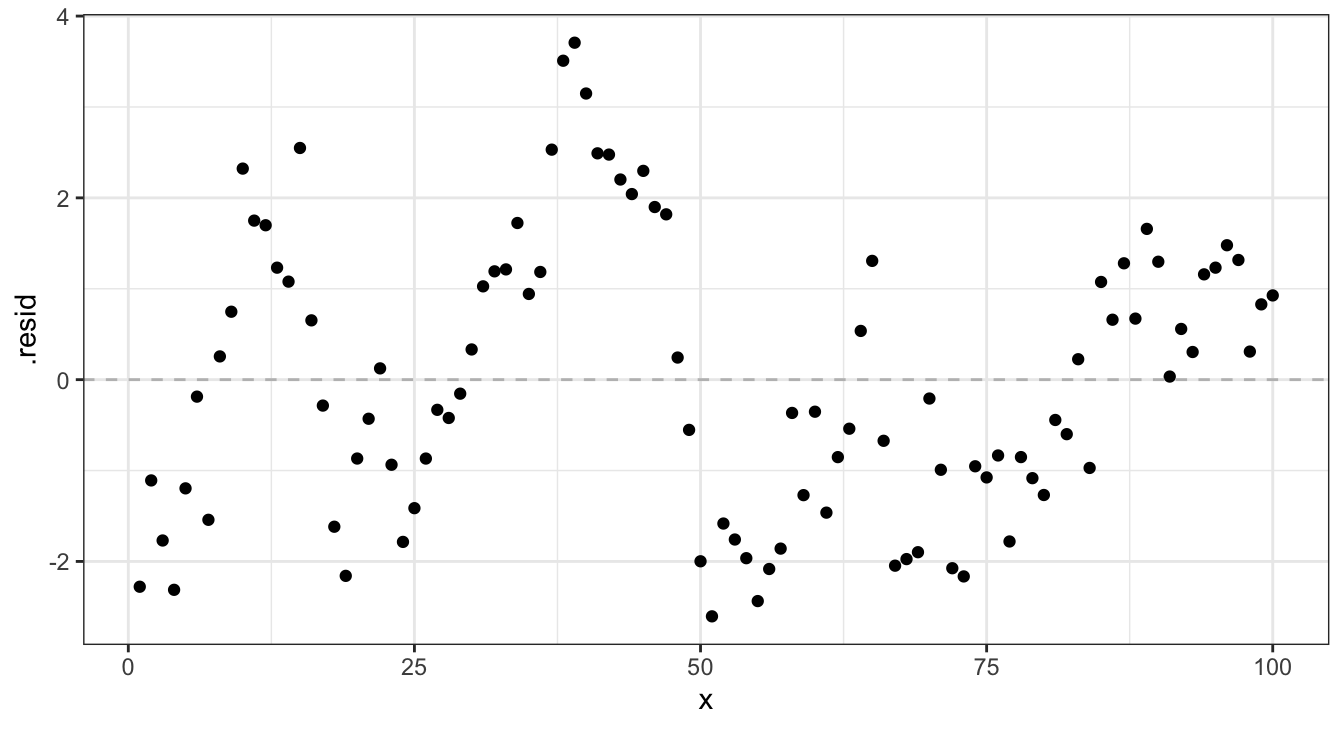
Residual posteriors - brms

b %>%
  tidybayes::residual_draws(newdata=d) |>
  ggplot(aes(x=x, y=.residual, group=x)) +
    tidybayes::stat_pointinterval() +
    geom_hline(yintercept = 0, color='grey', linetype=2)

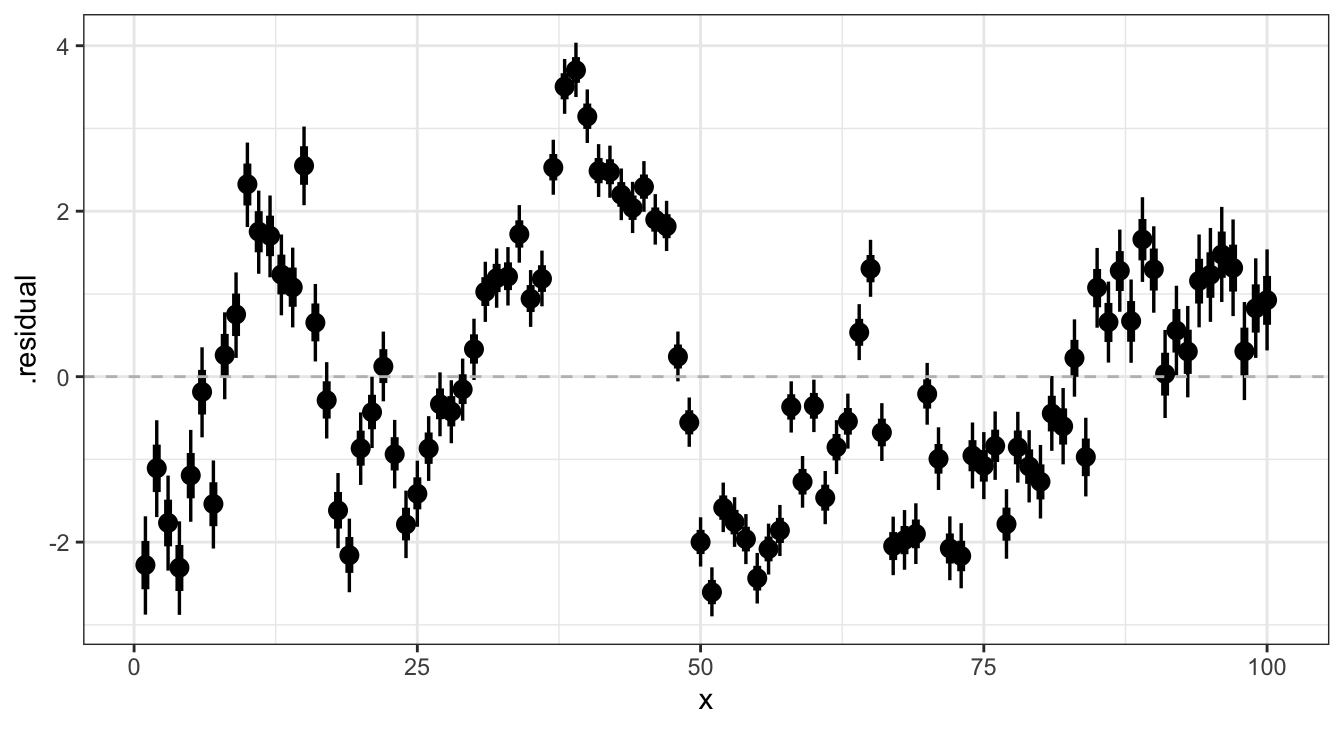
Model Evaluation

Model assessment

If we remember back to our first regression class, one common option is \(R^2\) which gives us the variability in \(y\) explained by our model.

Quick review:

\[ \underset{\text{Total}}{\sum_{i=1}^n \left(y_i - \bar{y}\right)^2} = \underset{\text{Model}}{\sum_{i=1}^n \left(\hat{y}_i - \bar{y}\right)^2} + \underset{\text{Error }}{\sum_{i=1}^n \left(y_i - \hat{y}_i\right)^2} \]

\[ R^2 = \frac{SS_{model}}{SS_{total}} = \frac{\sum_{i=1}^n \left(\hat{Y}_i - \bar{Y}\right)^2}{\sum_{i=1}^n \left(Y_i - \bar{Y}\right)^2} = \frac{\text{Var}(\hat{\boldsymbol{Y}}) }{ \text{Var}({\boldsymbol{Y}}) } = \text{Cor}(\boldsymbol{Y}, \hat{\boldsymbol{Y}})^2 \]

Some data prep

( b_post_full = b |>
    tidybayes::spread_draws(b_Intercept, b_x, sigma) |>
    tidyr::expand_grid(d) |>
    mutate(
      y_hat = b_Intercept + b_x * x,
      resid = y - y_hat
    )
)
## # A tibble: 400,000 × 10
##    .chain .iteration .draw b_Intercept    b_x sigma     x      y  y_hat  resid
##     <int>      <int> <int>       <dbl>  <dbl> <dbl> <int>  <dbl>  <dbl>  <dbl>
##  1      1          1     1      -0.961 0.0671  1.33     1 -3.24  -0.894 -2.35 
##  2      1          1     1      -0.961 0.0671  1.33     2 -2.00  -0.826 -1.18 
##  3      1          1     1      -0.961 0.0671  1.33     3 -2.59  -0.759 -1.84 
##  4      1          1     1      -0.961 0.0671  1.33     4 -3.07  -0.692 -2.38 
##  5      1          1     1      -0.961 0.0671  1.33     5 -1.88  -0.625 -1.26 
##  6      1          1     1      -0.961 0.0671  1.33     6 -0.807 -0.558 -0.248
##  7      1          1     1      -0.961 0.0671  1.33     7 -2.09  -0.491 -1.60 
##  8      1          1     1      -0.961 0.0671  1.33     8 -0.227 -0.424  0.197
##  9      1          1     1      -0.961 0.0671  1.33     9  0.333 -0.357  0.690
## 10      1          1     1      -0.961 0.0671  1.33    10  1.98  -0.290  2.27 
## # … with 399,990 more rows

Bayesian \(R^2\)

When we compute any statistic for our model we want to do so at each iteration so that we can obtain the posterior distribution of that particular statistic (e.g. the posterior distribution of \(R^2\) in this case).

( b_R2 = b_post_full %>%
    group_by(.iteration) %>%
    summarize(
      R2_classic = var(y_hat) / var(y),
      R2_bayes   = var(y_hat) / (var(y_hat) + var(resid))
    )
)
## # A tibble: 1,000 × 3
##    .iteration R2_classic R2_bayes
##         <int>      <dbl>    <dbl>
##  1          1      0.676    0.642
##  2          2      0.757    0.663
##  3          3      0.593    0.610
##  4          4      0.667    0.637
##  5          5      0.630    0.625
##  6          6      0.627    0.624
##  7          7      0.557    0.593
##  8          8      0.640    0.625
##  9          9      0.730    0.657
## 10         10      0.558    0.594
## # … with 990 more rows

Uh oh …

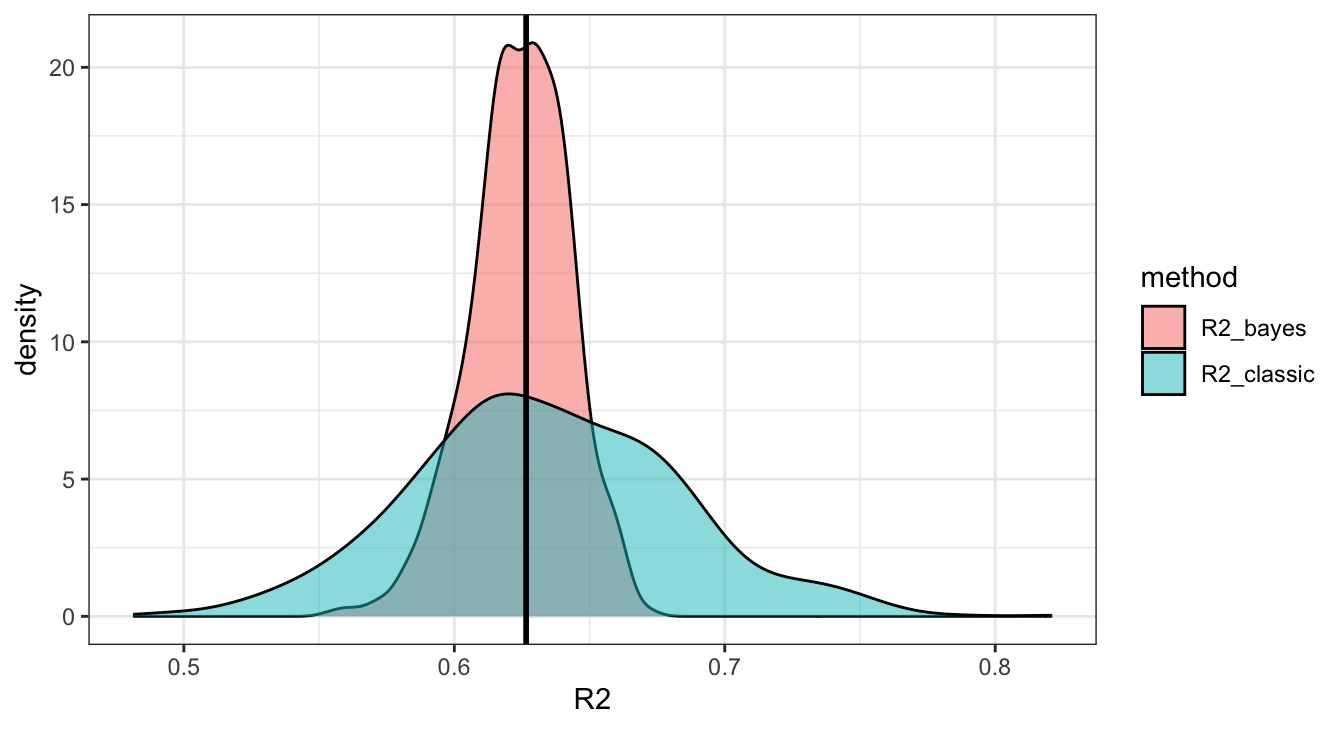
Sanity check

( l_pred = broom::augment(l) )
## # A tibble: 100 × 8
##         y     x .fitted .resid   .hat .sigma  .cooksd .std.resid
##     <dbl> <int>   <dbl>  <dbl>  <dbl>  <dbl>    <dbl>      <dbl>
##  1 -3.24      1  -0.962 -2.28  0.0394   1.53 0.0467       -1.51 
##  2 -2.00      2  -0.893 -1.11  0.0382   1.54 0.0107       -0.734
##  3 -2.59      3  -0.825 -1.77  0.0371   1.54 0.0264       -1.17 
##  4 -3.07      4  -0.757 -2.31  0.0359   1.53 0.0436       -1.53 
##  5 -1.88      5  -0.688 -1.20  0.0348   1.54 0.0113       -0.791
##  6 -0.807     6  -0.620 -0.187 0.0338   1.55 0.000266     -0.123
##  7 -2.09      7  -0.551 -1.54  0.0327   1.54 0.0175       -1.02 
##  8 -0.227     8  -0.483  0.256 0.0317   1.55 0.000466      0.169
##  9  0.333     9  -0.415  0.747 0.0307   1.55 0.00384       0.493
## 10  1.98     10  -0.346  2.32  0.0297   1.53 0.0358        1.53 
## # … with 90 more rows

broom::glance(l)$r.squared
## [1] 0.6265565

var(l_pred$.fitted) / var(l_pred$y)
## [1] 0.6265565

var(l_pred$.fitted) / (var(l_pred$.fitted) + var(l_pred$.resid))
## [1] 0.6265565

What if we collapsed first?

Here we calculate the posterior mean of \(\hat{y}\) and use that to estimate \(R^2\),

b_post_full %>%
  group_by(x) %>%
  summarize(
    y_hat = mean(y_hat),
    y = mean(y),
    resid = mean(y - y_hat),
    .groups = "drop"
  ) %>%
  summarize(
    R2_classic = var(y_hat) / var(y),
    R2_bayes   = var(y_hat) / (var(y_hat) + var(resid))
  )
## # A tibble: 1 × 2
##   R2_classic R2_bayes
##        <dbl>    <dbl>
## 1      0.627    0.627

Some problems with \(R^2\)

Some new issues,

• \(R^2\) doesn’t really make sense in the Bayesian context

  • multiple possible definitions with different properties

  • fundamental equality doesn’t hold anymore

  • Possible to have \(R^2 > 1\)

Some old issues,

• \(R^2\) always increases (or stays the same) when adding a predictor

• \(R^2\) is highly susceptible to over fitting

• \(R^2\) is sensitive to outliers

• \(R^2\) depends heavily on values of \(y\) (can differ for two equivalent models)

Some Other Metrics

Root Mean Square Error

The traditional definition of rmse is as follows

\[ \text{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=1}^n \left(y_i - \hat{y_i} \right)^2 } \]

In the bayesian context, we have posterior samples from each parameter / prediction of interest so we can express this as

\[ \frac{1}{m} \sum_{s=1}^{m} \sqrt{ \frac{1}{n} \sum_{i=1}^n \left(y_i - {\hat{y}}_{i,s} \right)^2 } \]

where \(m\) is the number of iterations and \(\hat{Y}^s_i\) is the prediction for \(Y_i\) at iteration \(s\).

Continuous Rank Probability Score

Another approach is the continuous rank probability score which comes from the probabilistic forecasting literature, it compares the full posterior predictive distribution to the observation / truth.

\[ \text{CRPS} = \int_{-\infty}^\infty \left(F_{\hat{y}}(z) - {1}_{z \geq y}\right)^2 dz \]

where \(F_{\hat{y}}\) is the CDF of \(\hat{y}\) (the posterior predictive distribution for \(y\)) and \({1}_{z \geq Y}\) is an indicator function which equals 1 when \(z \geq y\), the true/observed value of \(y\).

Since this calculates a score for a single probabilistic prediction we can naturally extend it to multiple predictions by calculating an average CRPS \[ \frac{1}{n} \sum_{i=1}^n \int_{-\infty}^\infty \left(F_{\hat{y}_i}(z) - {1}_{z \geq y_i}\right)^2 dz \]

CDF vs Indicator

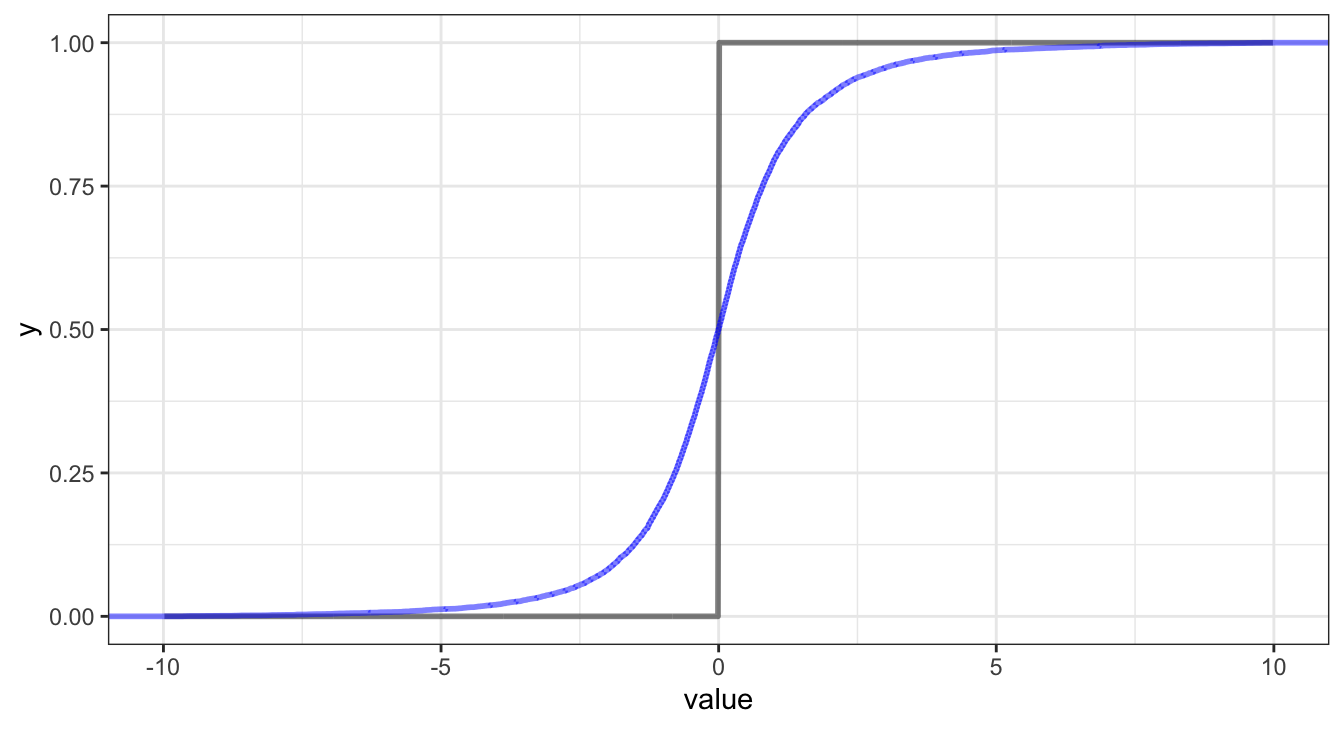
Empirical CDF vs Indicator

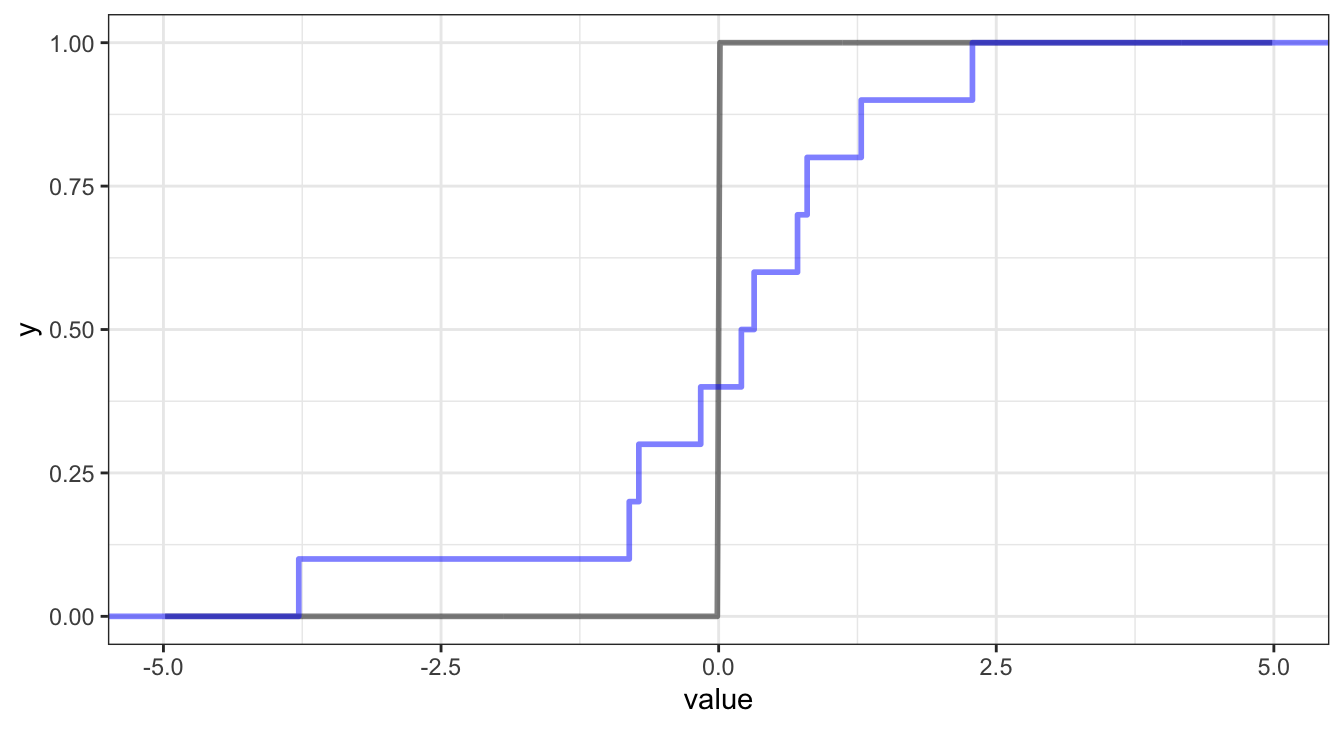
Accuracy vs. Precision

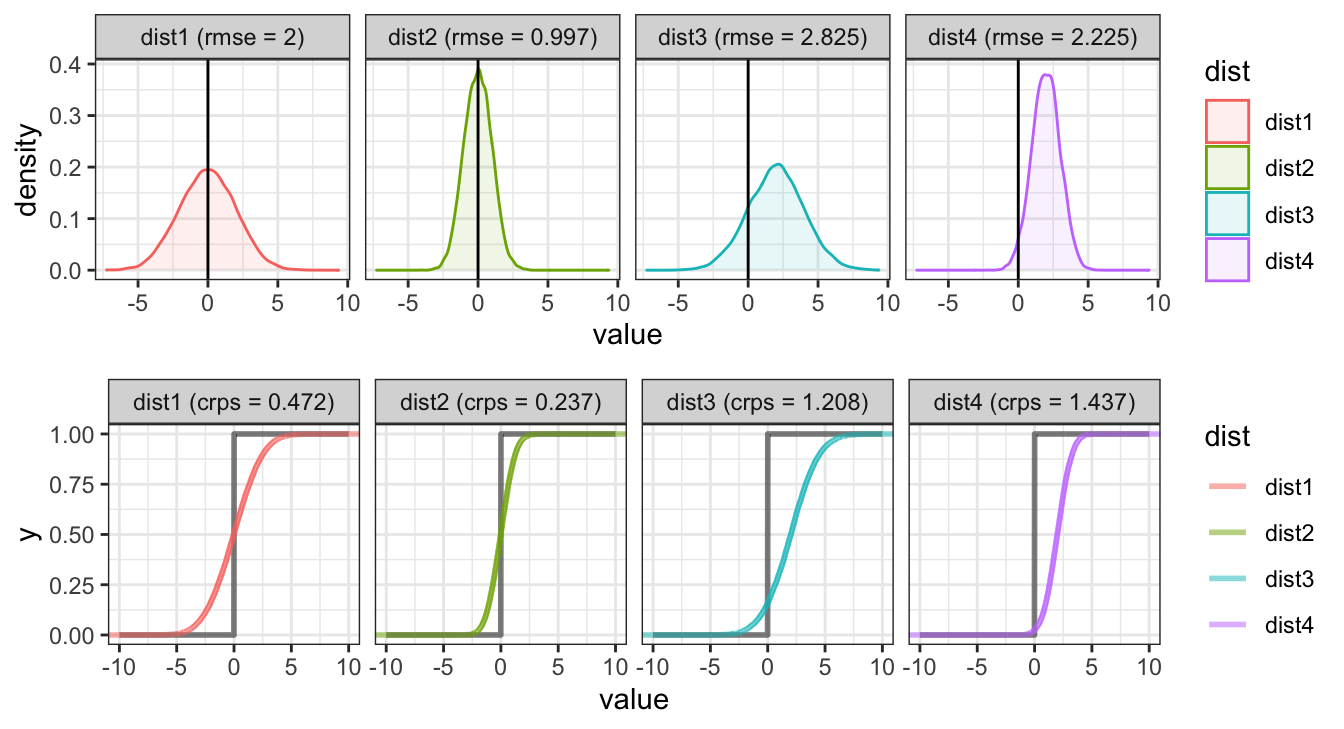
Empirical Coverage

One final method, which assesses model calibration is to examine how well credible intervals, derived from the posterior predictive distributions of the \(y\)s, capture the true/observed values.

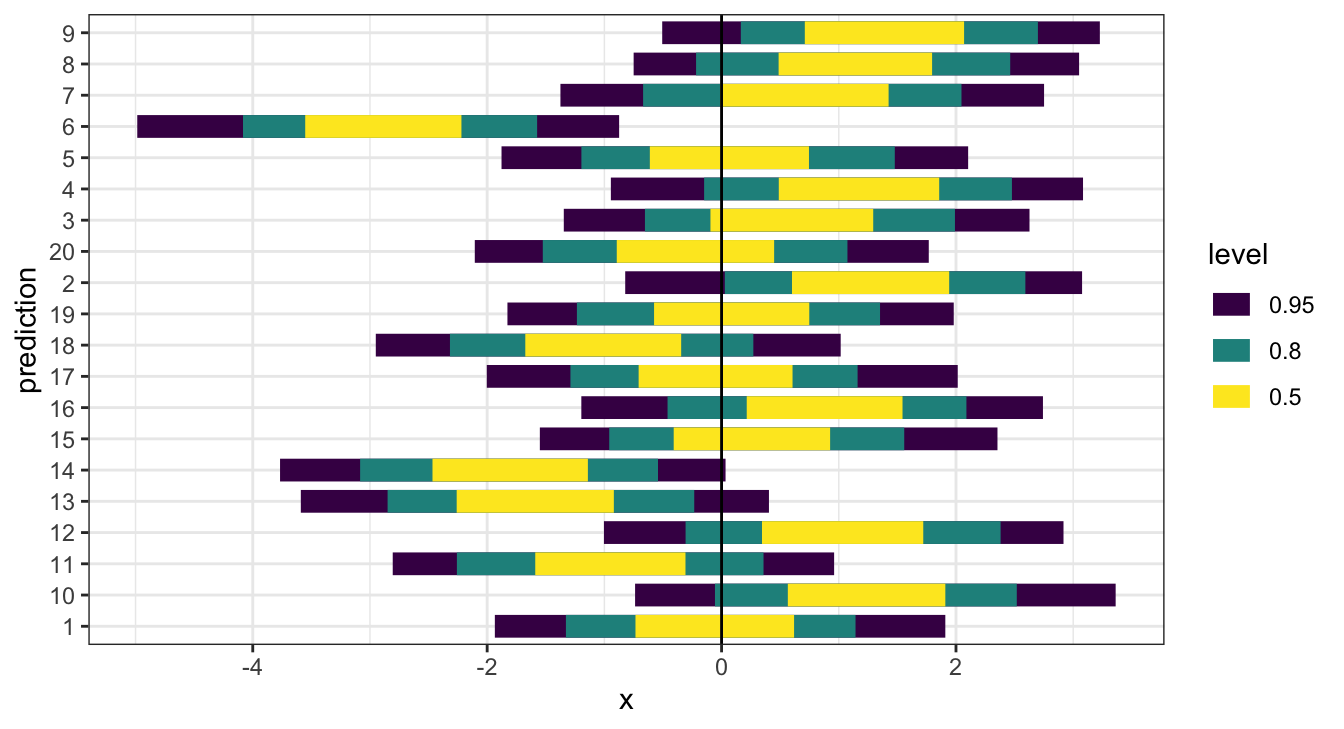
Back to our example

RMSE - \(\hat{y}\)

broom::augment(l) |>
  yardstick::rmse(y, .fitted)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard        1.52

( b_rmse = b_post_full %>%
    group_by(.chain, .iteration) %>%
    summarize(
      rmse = sqrt( sum( (y - y_hat)^2 ) / n())
    )
)
## # A tibble: 4,000 × 3
## # Groups:   .chain [4]
##    .chain .iteration  rmse
##     <int>      <int> <dbl>
##  1      1          1  1.53
##  2      1          2  1.53
##  3      1          3  1.53
##  4      1          4  1.53
##  5      1          5  1.53
##  6      1          6  1.53
##  7      1          7  1.53
##  8      1          8  1.53
##  9      1          9  1.53
## 10      1         10  1.53
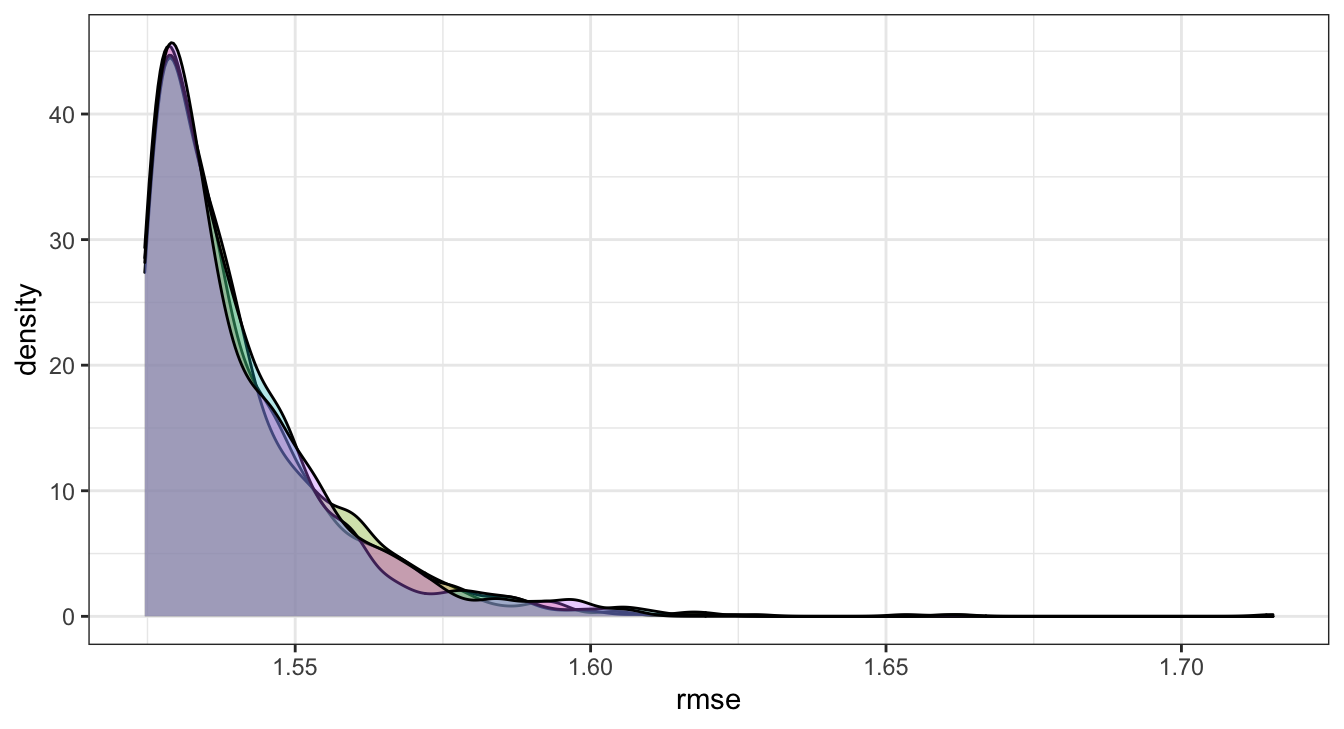
## # … with 3,990 more rows

RMSE - \(\hat{y}\) - Results

b_rmse |> 
  group_by(.chain) |> 
  summarize(post_mean = mean(rmse))
## # A tibble: 4 × 2
##   .chain post_mean
##    <int>     <dbl>
## 1      1      1.54
## 2      2      1.54
## 3      3      1.54
## 4      4      1.54

ggplot(b_rmse) +
  geom_density(
    aes(x=rmse, fill=as.factor(.chain)), 
    alpha=0.33
  ) +
  guides(fill="none")

CRPS - \(\hat{y}\)

( b_crps = b_post_full |>
    group_by(.chain, x) |>
    summarise(
      crps = calc_crps(y_hat, y)
    )
)
## # A tibble: 400 × 3
## # Groups:   .chain [4]
##    .chain     x  crps
##     <int> <int> <dbl>
##  1      1     1 2.10 
##  2      1     2 0.934
##  3      1     3 1.60 
##  4      1     4 2.14 
##  5      1     5 1.03 
##  6      1     6 0.113
##  7      1     7 1.38 
##  8      1     8 0.156
##  9      1     9 0.599
## 10      1    10 2.18 
## # … with 390 more rows

b_crps |>
  group_by(.chain) |>
  summarize( 
    avg_crps = mean(crps)
  )
## # A tibble: 4 × 2
##   .chain avg_crps
##    <int>    <dbl>
## 1      1     1.19
## 2      2     1.19
## 3      3     1.19
## 4      4     1.19

Empirical Coverage - \(\hat{y}\)

( b_cover = b_post_full %>% 
    group_by(x, y) %>% 
    tidybayes::mean_hdi(
      y_hat, .prob = c(0.5,0.9,0.95)
    ) 
)
## # A tibble: 300 × 8
##        x      y  y_hat .lower .upper .width .point .interval
##    <int>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
##  1     1 -3.24  -0.963 -1.14  -0.735    0.5 mean   hdi      
##  2     2 -2.00  -0.894 -1.07  -0.669    0.5 mean   hdi      
##  3     3 -2.59  -0.826 -1.02  -0.630    0.5 mean   hdi      
##  4     4 -3.07  -0.758 -0.947 -0.562    0.5 mean   hdi      
##  5     5 -1.88  -0.689 -0.847 -0.467    0.5 mean   hdi      
##  6     6 -0.807 -0.621 -0.771 -0.398    0.5 mean   hdi      
##  7     7 -2.09  -0.552 -0.745 -0.378    0.5 mean   hdi      
##  8     8 -0.227 -0.484 -0.667 -0.306    0.5 mean   hdi      
##  9     9  0.333 -0.415 -0.594 -0.240    0.5 mean   hdi      
## 10    10  1.98  -0.347 -0.521 -0.174    0.5 mean   hdi      
## # … with 290 more rows

Empirical Coverage - \(\hat{y}\) - Results

b_cover %>%
  mutate(contains = y >= .lower & y <= .upper) %>%
  group_by(prob = .width) %>%
  summarize(
    emp_cov = sum(contains)/n()
  )
## # A tibble: 3 × 2
##    prob emp_cov
##   <dbl>   <dbl>
## 1  0.5     0.02
## 2  0.9     0.11
## 3  0.95    0.14

What went wrong now?